为什么跳表能替代红黑树？Redis Sorted Set 背后的数据结构

1. 前言

Redis 的 Sorted Set（zset）是非常常用的数据类型：它既要支持按 score 排序的范围查询（range by score / by rank），又要支持按成员（member）快速查找与更新。很多人看到“有序集合”会首先想到平衡二叉树（如红黑树、AVL），但 Redis 最终选择了 跳表（skip list）。本文从理论与工程实现角度解释为什么跳表能替代红黑树，并给出一个可运行的代码实战（简化版跳表实现 + 使用示例），帮助你把概念落地。

2. 基础回顾

2.1 红黑树简介

• 红黑树是自平衡二叉查找树，保证 O(log n) 的查找、插入、删除（最坏情形）。
• 特点：树形结构，旋转与颜色翻转维护平衡。实现相对复杂，尤其在插入/删除时需要多处调整。
• 优点：最坏情况时间保证好；单节点额外空间很少（父/左右/颜色）。

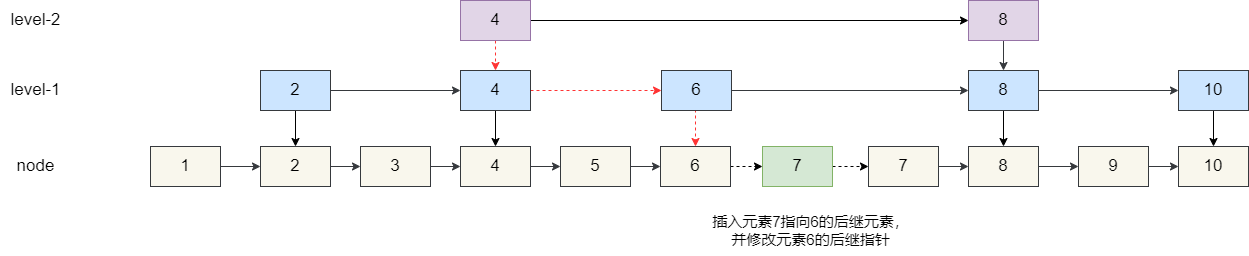
2.2 跳表简介

• 跳表是一种概率型数据结构，基于多级链表：最高层稀疏，底层是完整的有序链表。每个元素被随机提升到若干层（几率通常为 1/2）。
• 平均时间复杂度：O(log n)（查找/插入/删除）。最坏情况退化为 O(n)，但概率极低（可通过修改参数控制）。
• 优点：实现相对直观（链表+指针），插入/删除只需局部操作；容易扩展以记录跨度（span），支持按排名的快速定位；并发友好（更适合部分并发方案）。

3. 跳表 vs 红黑树：从理论到实践

3.1 平均/最坏时间复杂度

• 红黑树：查找/插入/删除均为 最坏 O(log n)。
• 跳表：平均为 O(log n)，最坏 O(n)（极低概率）。在工程实践中，这种随机化带来的最坏情况通常可忽略。

3.2 实现复杂性与可维护性

• 红黑树：插入/删除涉及多种旋转与颜色规则，代码复杂且容易出错。
• 跳表：主要是指针调整（链表插入/删除），代码更直观，长远维护成本较低。对于工程团队来说，可读性与可维护性是重要考量。

3.3 并发场景下的优势

• 跳表天然是分层链表结构，更容易实现并发友好的读/写（例如 lock-free 或分段锁），而平衡树的旋转会触及多处节点，增加并发实现复杂度。
• Redis 虽然是单线程模型，但跳表的简单局部更新使得实现和调优更直接。

3.4 空间消耗

• 跳表需要额外的指针（多层指针）和可能的跨度数组，空间比单个红黑树节点要多。实际工程中这是可以接受的折中（内存换取实现复杂度/性能）。
• Redis 在 zset 中用跳表 + 哈希表的组合：哈希表用于按成员 O(1) 定位，跳表用于按 score 排序与范围/排名操作。

3.5 常数因子与缓存友好性

• 跳表内部是链式布局，内存跳跃小，缓存局部性比树形指针跳转好（在 CPU cache 层面常常表现更优）。
• 常数因子小、代码简单通常使跳表在实际场景中比复杂树结构拥有更好的工程性能。

4. Redis 的选择：为什么 Redis 用跳表实现 Sorted Set（zset）

4.1 zset 的 API 要求（典型）

• ZADD：按 member 插入或更新 score。
• ZRANK / ZREVRANK：按成员返回排名（rank）。
• ZRANGE / ZRANGEBYSCORE：按 rank 或 score 返回范围元素。
• ZREM：删除成员。
• 要求：既能按 member 快速定位（用于更新/删除），又能按 score 做有序遍历/范围操作。

4.2 跳表如何满足这些需求

• Redis 的实现是：一个哈希表（dict）映射 member -> score，以及一个跳表根据 (score, member) 排序。这样：

  • 通过哈希表可以 O(1) 定位 member 是否存在及其 score（便于更新）。
  • 通过跳表可以按 score 做有序操作、计算排名、范围遍历。

• 这种双结构设计把两者优势结合起来，满足 zset 的所有 API 要求并保证良好的性能。

4.3 Redis 的实现细节（简要）

• 跳表节点包含：score, member, 多级 forward 指针、每层的 span（用于快速计算 rank）。
• span 记录跨越的底层节点数量，使得在查找时可以累加跨度快速得出排名（而不必从头遍历）。
• 随机层数用几率 P = 0.25（或 0.5），以及 MAX_LEVEL（如 32）限制高度。

5. 代码实战 — Python 简化跳表实现（支持插入、删除、按 score 范围查询、按 member 查找和排名）

下面给出一个可运行的简化实现，帮助你理解跳表在 zset 场景的关键做法（注意：为便于教学，略去了某些 Redis 级别的优化与边界处理）。

# skiplist_demo.py
import random
from typing import Any, List, Optional, Tuple

MAX_LEVEL = 16
P = 0.5

class SkipNode:
    def __init__(self, score: float, member: Any, level: int):
        self.score = score
        self.member = member
        # forward pointers for each level
        self.forward = [None] * level
        # span for each level (number of nodes skipped at this level)
        self.span = [0] * level

class SkipList:
    def __init__(self):
        self.level = 1
        self.head = SkipNode(float('-inf'), None, MAX_LEVEL)
        self.length = 0

    def random_level(self) -> int:
        lvl = 1
        while random.random() < P and lvl < MAX_LEVEL:
            lvl += 1
        return lvl

    def insert(self, score: float, member: Any) -> None:
        update = [None] * MAX_LEVEL
        rank = [0] * MAX_LEVEL
        x = self.head

        # find insertion points and rank spans
        for i in reversed(range(self.level)):
            # accumulate rank for this level
            if i < self.level - 1:
                rank[i] = rank[i+1]
            else:
                rank[i] = 0
            while x.forward[i] and (x.forward[i].score < score or
                                    (x.forward[i].score == score and x.forward[i].member < member)):
                rank[i] += x.span[i]
                x = x.forward[i]
            update[i] = x

        # random level for new node
        lvl = self.random_level()
        if lvl > self.level:
            for i in range(self.level, lvl):
                update[i] = self.head
                update[i].span[i] = self.length
            self.level = lvl

        # create node
        new_node = SkipNode(score, member, lvl)
        for i in range(lvl):
            new_node.forward[i] = update[i].forward[i]
            update[i].forward[i] = new_node

            # span updates:
            # new_node.span[i] should be set to the number of nodes that update[i] skipped minus ranks
            new_node.span[i] = update[i].span[i] - (rank[0] - rank[i]) if update[i].span[i] else 0
            update[i].span[i] = (rank[0] - rank[i]) + 1

        # for levels above new node, increase span by 1
        for i in range(lvl, self.level):
            update[i].span[i] += 1

        self.length += 1

    def delete(self, score: float, member: Any) -> bool:
        update = [None] * MAX_LEVEL
        x = self.head
        found = False
        for i in reversed(range(self.level)):
            while x.forward[i] and (x.forward[i].score < score or
                                    (x.forward[i].score == score and x.forward[i].member < member)):
                x = x.forward[i]
            update[i] = x

        target = x.forward[0]
        if target and target.score == score and target.member == member:
            found = True
            for i in range(self.level):
                if update[i].forward[i] == target:
                    update[i].span[i] += target.span[i] - 1
                    update[i].forward[i] = target.forward[i]
                else:
                    update[i].span[i] -= 1
            # adjust level
            while self.level > 1 and not self.head.forward[self.level-1]:
                self.level -= 1
            self.length -= 1
        return found

    def iter_range_by_score(self, min_score: float, max_score: float) -> List[Tuple[float, Any]]:
        res = []
        x = self.head
        # go down to level 0 and forward until reaching first >= min_score
        for i in reversed(range(self.level)):
            while x.forward[i] and x.forward[i].score < min_score:
                x = x.forward[i]

        x = x.forward[0]
        while x and x.score <= max_score:
            res.append((x.score, x.member))
            x = x.forward[0]
        return res

    def rank(self, score: float, member: Any) -> Optional[int]:
        """Return 0-based rank if found, or None."""
        x = self.head
        rank = 0
        for i in reversed(range(self.level)):
            while x.forward[i] and (x.forward[i].score < score or
                                    (x.forward[i].score == score and x.forward[i].member <= member)):
                rank += x.span[i]
                x = x.forward[i]
                # if matched exactly, check
                if x.score == score and x.member == member:
                    return rank - 1  # convert to 0-based
        return None

# A simple zset-like wrapper that keeps a dict for member->score and a skiplist for ordering
class MiniZSet:
    def __init__(self):
        self.map = {}  # member -> score
        self.sl = SkipList()

    def zadd(self, member: str, score: float) -> None:
        if member in self.map:
            # remove old
            old = self.map[member]
            self.sl.delete(old, member)
        self.map[member] = score
        self.sl.insert(score, member)

    def zrem(self, member: str) -> bool:
        if member not in self.map:
            return False
        score = self.map.pop(member)
        return self.sl.delete(score, member)

    def zrangebyscore(self, min_score: float, max_score: float) -> List[Tuple[float, Any]]:
        return self.sl.iter_range_by_score(min_score, max_score)

    def zrank(self, member: str) -> Optional[int]:
        if member not in self.map:
            return None
        score = self.map[member]
        return self.sl.rank(score, member)

# ------------ Demo ------------
if __name__ == "__main__":
    z = MiniZSet()
    z.zadd("alice", 10)
    z.zadd("bob", 20)
    z.zadd("carol", 15)
    z.zadd("dave", 20)     # same score as bob, member lexicographically used to break ties

    print("zrange 10..20:", z.zrangebyscore(10, 20))
    print("rank of carol:", z.zrank("carol"))
    print("rank of bob:", z.zrank("bob"))
    print("remove bob:", z.zrem("bob"))
    print("zrange 0..100:", z.zrangebyscore(0, 100))

代码说明（要点）

• SkipList 中 span 的设计可用于快速计算前缀长度（从而得到 rank）。这也是 Redis 跳表实现里的关键技巧。
• MiniZSet 同时维护一个 dict（O(1) 查 member）和跳表（按 score 有序），完全模拟 zset 的思路。
• 生产级 Redis 实现更加复杂（内存布局优化、随机数控制、内存回收、并发与持久化兼容、更多边界校验）。

6. 工程实践与调优建议

• 如果对最坏时间要求极其严格（不能接受概率退化），使用红黑树或 B 树可以更稳妥。但如果工程上更看重实现复杂度、常数因子、以及 range 操作效率，跳表是更好的选择。
• 在内存敏感环境，可以调低跳表的 MAX_LEVEL 或调整 P（概率），以减少指针开销。
• 跳表非常容易配合哈希表实现一套完备的有序集合（正如 Redis 做的），这是生产可用的折中方案。
• 若要在并发环境下优化读写，可考虑分段锁或无锁跳表设计（研究方向较多）。

7. 总结

跳表之所以能替代红黑树，并被 Redis 用于 Sorted Set，原因可以概括为：实现更简单、常数因子小、支持高效的范围与排名操作、并且更容易在工程中维护和并发化。Redis 采用跳表 + 哈希表的组合，把两种结构的优势结合起来，既保证了按 member 的 O(1) 定位，又支持按 score 的有序操作和排名查询。

如果你想，我可以：

• 把上面的跳表实现改成更接近 Redis 的 C 版本伪代码（帮助理解 Redis 源码）。
• 或者把 Python 实现扩展出更完整的单元测试与基准测试代码，让你能在本地跑性能对比（例如与 sortedcontainers、或自己实现的平衡树比较）。哪一种你更想看？