基于图存储结构差异的复杂网络遍历效率比较研究
基于图存储结构差异的复杂网络遍历效率比较研究
在图结构中,如何高效存储边信息直接影响图算法的性能。无论是 BFS / DFS 遍历、最短路 Dijkstra、最小生成树 Kruskal / Prim,底层都离不开图的存储结构选择。
本文将分别介绍三种常用图存储方式:
- 邻接矩阵(Adjacency Matrix)
- 邻接表(Adjacency List)
- 链式前向星(Forward Star)
并通过示例代码演示它们的构建和使用方式,帮助你全面掌握三者的本质差异与应用场景。
一、邻接矩阵(Adjacency Matrix)
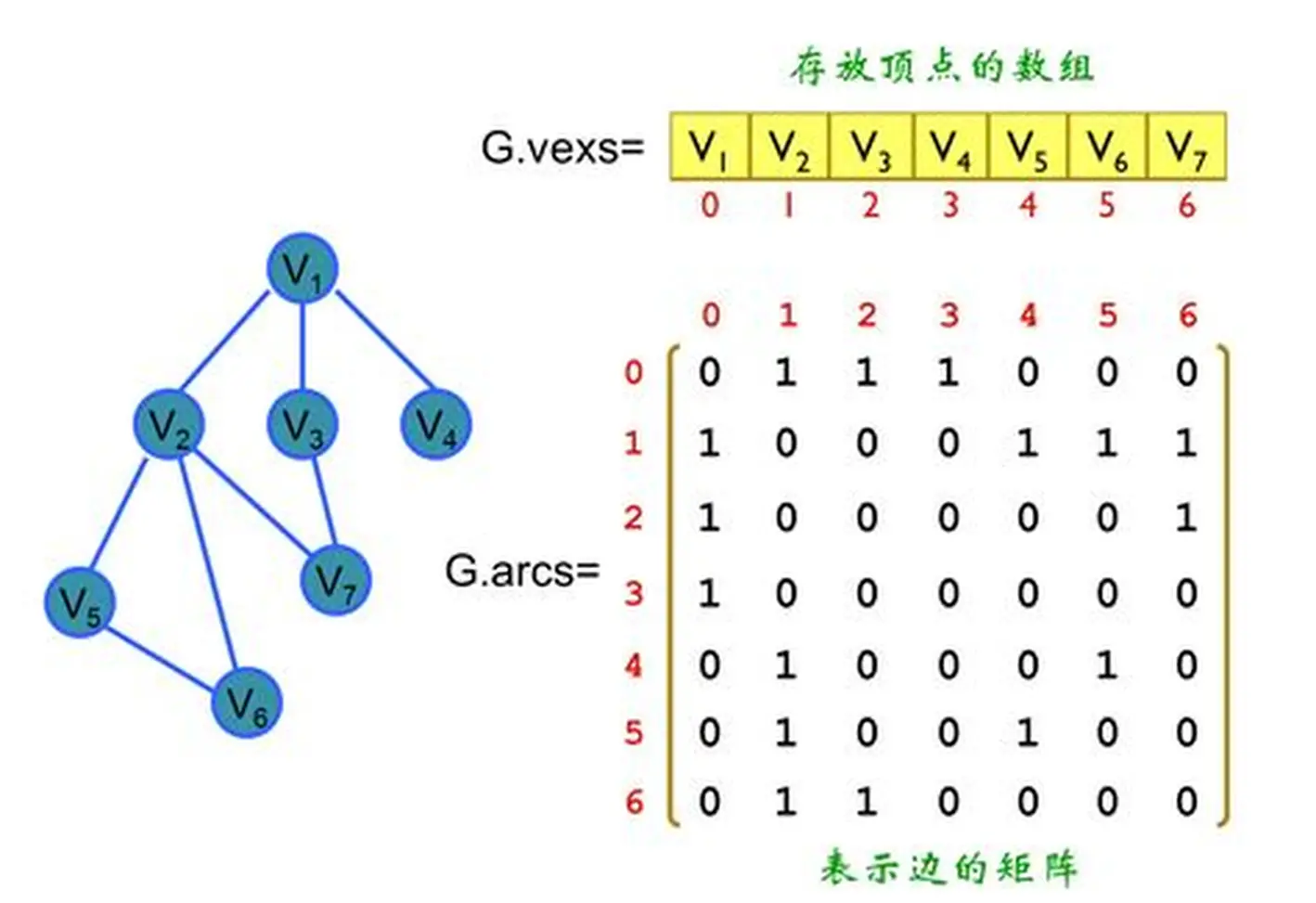
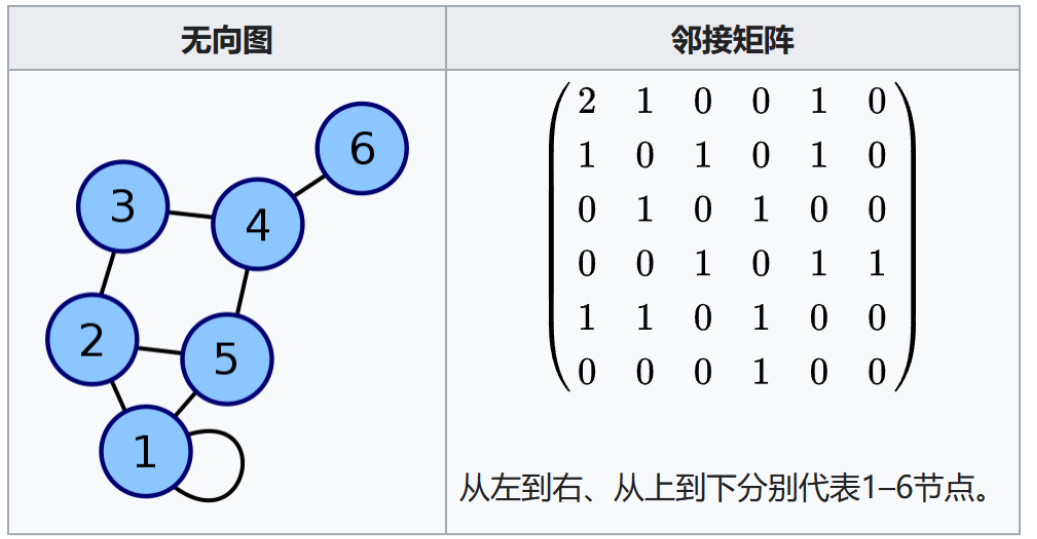
1.1 概念
邻接矩阵使用一个 n × n 的二维矩阵存储图,适合节点数量不大但边较多(稠密图)的情况。
若节点 u 和 v 有边,则:
matrix[u][v] = 1 (无权图)
matrix[u][v] = w (带权图)
否则为 0 或 ∞。
1.2 空间复杂度
O(n^2)
因此不适合大量节点的稀疏图场景。
1.3 示例代码(无向图)
#include <iostream>
using namespace std;
const int N = 5;
int g[N][N]; // 邻接矩阵
int main() {
// 添加边 (0-1), (0-2), (1-3)
g[0][1] = g[1][0] = 1;
g[0][2] = g[2][0] = 1;
g[1][3] = g[3][1] = 1;
// 输出邻接矩阵
for(int i = 0; i < N; i++) {
for(int j = 0; j < N; j++)
cout << g[i][j] << " ";
cout << endl;
}
}
二、邻接表(Adjacency List)
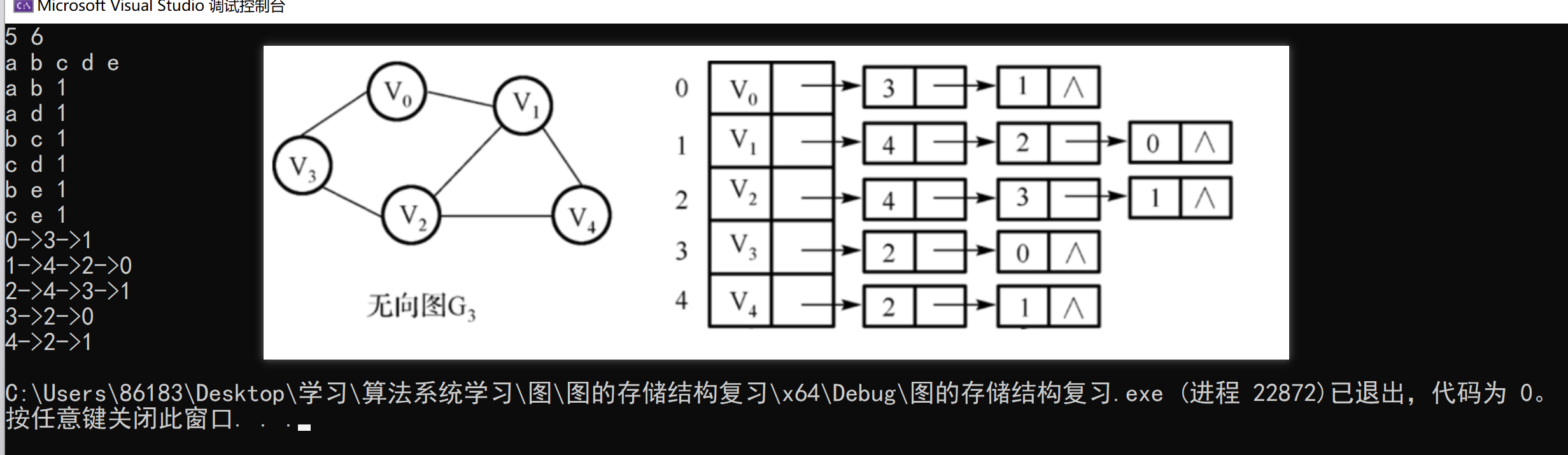
2.1 概念
邻接表使用数组 + 链表或 vector 的方式存储图,每个节点只存储其相邻节点,适合 稀疏图。
结构示意:
0 -> 1 -> 2
1 -> 0 -> 3
2 -> 0
3 -> 1
2.2 空间复杂度
O(n + m)
其中 m 为边数,远小于 n^2。
2.3 示例代码
#include <iostream>
#include <vector>
using namespace std;
const int N = 5;
vector<int> g[N]; // 邻接表
int main() {
g[0].push_back(1);
g[0].push_back(2);
g[1].push_back(0);
g[1].push_back(3);
// 输出邻接表
for(int i = 0; i < N; i++) {
cout << i << ": ";
for(int v : g[i])
cout << v << " ";
cout << endl;
}
}
三、链式前向星(Forward Star)
3.1 概念
链式前向星是一种压缩版邻接表,常用于 图论竞赛 / 最短路径 / 最大流 等需要极高性能的场景。
它用三个数组实现:
| 数组 | 含义 |
|---|---|
head[u] |
节点 u 的第一条边在数组中的下标 |
to[i] |
第 i 条边指向的节点 |
next[i] |
同一个起点 u 的下一条边的编号 |
插边流程:相当于 链表头插法
to[cnt] = v
next[cnt] = head[u]
head[u] = cnt
cnt++
3.2 示例代码
#include <iostream>
using namespace std;
const int N = 100;
int head[N], to[N], nxt[N];
int cnt = 0; // 边数量指针
void addEdge(int u, int v) {
to[cnt] = v;
nxt[cnt] = head[u];
head[u] = cnt;
cnt++;
}
int main() {
// 初始化 head 数组为 -1
fill(head, head + N, -1);
// 添加有向边 0->1, 0->2, 1->3
addEdge(0, 1);
addEdge(0, 2);
addEdge(1, 3);
// 遍历
for(int u = 0; u < 5; u++) {
cout << u << ": ";
for(int i = head[u]; i != -1; i = nxt[i])
cout << to[i] << " ";
cout << endl;
}
}
四、三种存储方式对比总结
| 存储方式 | 空间复杂度 | 适用场景 | 优点 | 缺点 |
|---|---|---|---|---|
| 邻接矩阵 | O(n²) | 稠密图 | 查询是否有边快 | 空间浪费严重 |
| 邻接表 | O(n + m) | 稀疏图(常用) | 空间高效 | 查询是否有边需遍历 |
| 链式前向星 | O(n + m) | 算法竞赛、高性能图算法 | 遍历快、Cache 友好 | 编码复杂,调试难 |
五、总结
图的存储结构不是可有可无,而是计算效率的关键:
- 节点少、边多 → 邻接矩阵
- 节点多、边少 → 邻接表
- 追求极致性能 → 链式前向星
建议在日常开发中优先使用邻接表,在 ACM / 蓝桥杯 / 力扣图论高性能场景 中再切换为 链式前向星。
图的存储方式直接影响图算法的效率与实现复杂度。邻接矩阵结构简单,适用于节点较少且边较密的图,但空间消耗大;邻接表更加灵活,能在稀疏图中有效节省空间,是实际工程与日常开发中最常用的方式;而链式前向星则在邻接表基础上进一步优化了存储与遍历性能,非常适合在竞赛与高性能图算法中使用。理解并根据具体场景选择合适的存储方式,能够让我们在处理图问题时做到既高效又优雅。
图的存储结构不是单纯的数据组织方式选择,而是与算法效率、内存占用以及工程实现复杂度密切相关的关键因素。在理解图论问题时,必须意识到:图本质上由节点与边构成,而如何存储边的关系会直接决定我们能以多快的速度进行访问、遍历、搜索和计算。
邻接矩阵的优点在于结构简单、查边操作时间复杂度为 O(1),即只需通过 matrix[u][v] 便能快速判断两个节点是否相连,因此适用于边密集、节点数量较小的场景,例如某些完全图或网络连通度较高的系统;但其 O(n²) 的空间开销在稀疏图中显得非常浪费,扩展性有限。
邻接表则恰恰反过来,它只存储每个节点真实存在的边,大幅降低空间占用,使得其成为稀疏图的最佳选择。各类 BFS、DFS、Dijkstra、拓扑排序等经典算法,在邻接表上的时间和空间效率都非常理想,因此在工业界、科研以及常规开发场景中被广泛采用。
链式前向星可以视作邻接表的数组化与性能优化版本。它利用连续内存存储节点边信息,因此遍历效率高、缓存友好、插入操作常数级,非常适合对图算法性能要求极高的场景,例如竞赛、图优化、最短路、网络流等。虽然编码与调试相对邻接表复杂一些,但在性能敏感领域处于主流地位。
综上,在实际开发或学习中,我们需要做到:理解差异、根据场景选择、必要时进行结构优化。只要选择合适的存储方式,就能让图相关算法在复杂性和效率上都达到最优水平,从而为后续处理更复杂的最短路径、最小生成树、网络流与搜索优化奠定扎实基础。
- 点赞
- 收藏
- 关注作者


评论(0)