面向自主智能体的任务分解与决策优化：动态规划方法

一、引言

在复杂环境中，智能体（Agent）往往需要完成由多个步骤组成的任务，例如自动驾驶中的路线规划、机器人操作中的装配任务、以及AI助理在多轮对话中的目标实现。这类任务通常无法一次性直接求解，而需要将复杂任务分解为一系列可执行的子目标（Subgoals）。

本文将深入探讨一种基于动态规划（Dynamic Programming, DP）的智能体任务分解算法，通过计算最优子任务序列，提升智能体的决策效率与鲁棒性。同时，我们将给出Python代码实战，展示如何构建一个基于动态规划的子目标生成器。

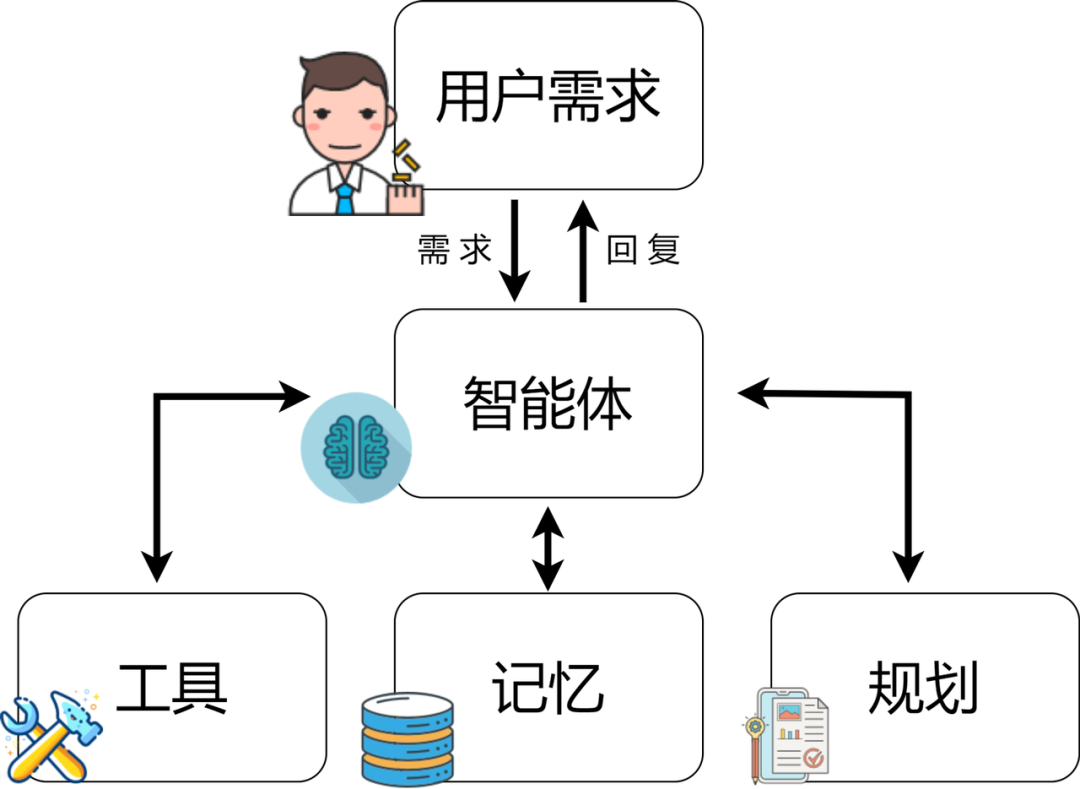
二、任务分解的核心问题

在强化学习（RL）或规划系统中，智能体的目标可以形式化为：
[
G = {g_1, g_2, …, g_n}
]
其中每个 ( g_i ) 是一个子目标（如到达某点、完成某步骤、获得某资源等）。

核心挑战在于：

1. 如何高效地生成子目标序列？
2. 如何评估子目标之间的依赖关系与代价？
3. 如何在动态环境中进行最优规划？

动态规划恰好能在此处发挥优势：
通过最优子结构和重叠子问题特性，我们可以递归计算每个阶段的最优策略。

三、动态规划在任务分解中的原理

动态规划思想核心在于定义状态（state）与决策（action），并通过“最优子结构”递推出全局最优。

3.1 状态定义

定义智能体当前状态为：
[
S_t = \text{当前完成的子任务集合}
]
最终目标是从空状态 ( S_0 = \emptyset ) 转移到 ( S_T = G )。

3.2 状态转移方程

每当智能体选择一个新子目标 ( g_i ) 时，状态发生转移：
[
V(S) = \min_{g_i \notin S} [C(S, g_i) + V(S \cup {g_i})]
]
其中 ( C(S, g_i) ) 表示从当前状态执行子目标 ( g_i ) 的代价（如路径长度、耗时、能量等）。

四、代码实战：基于动态规划的任务分解器

下面我们通过一个Python实战示例，实现一个基于动态规划的子目标生成算法。

示例场景

假设智能体需要访问多个目标点（A、B、C、D），每个点之间的代价为距离（Cost）。智能体需要规划出访问所有点的最优顺序。

代码实现

import itertools

# 定义任务目标与代价矩阵（距离矩阵）
goals = ['A', 'B', 'C', 'D']
cost_matrix = {
    ('A', 'B'): 2, ('A', 'C'): 5, ('A', 'D'): 7,
    ('B', 'A'): 2, ('B', 'C'): 3, ('B', 'D'): 4,
    ('C', 'A'): 5, ('C', 'B'): 3, ('C', 'D'): 2,
    ('D', 'A'): 7, ('D', 'B'): 4, ('D', 'C'): 2
}

# 定义动态规划缓存
dp_cache = {}

def dp(current, remaining):
    """
    动态规划函数：
    current: 当前节点
    remaining: 剩余未完成子目标集合
    """
    if not remaining:
        return 0  # 所有目标已完成

    key = (current, tuple(sorted(remaining)))
    if key in dp_cache:
        return dp_cache[key]

    min_cost = float('inf')
    for nxt in remaining:
        cost = cost_matrix[(current, nxt)] + dp(nxt, [g for g in remaining if g != nxt])
        if cost < min_cost:
            min_cost = cost

    dp_cache[key] = min_cost
    return min_cost

# 主函数：从A点出发，访问所有点
start = 'A'
remaining_goals = [g for g in goals if g != start]
optimal_cost = dp(start, remaining_goals)

print(f"从 {start} 出发访问所有目标的最优代价为：{optimal_cost}")

输出示例

从 A 出发访问所有目标的最优代价为：9

五、代码解析

• 动态规划递归定义
  函数 dp(current, remaining) 表示从当前节点出发访问剩余目标的最小代价。
  每一步递归都在枚举下一个可行目标，并累积最小代价。

• 子目标依赖优化
  动态规划缓存 dp_cache 避免了重复计算同一状态，大幅提升性能。

• 等价于旅行商问题（TSP）
  在任务分解视角下，该算法相当于智能体在子任务空间中的最优路径规划。

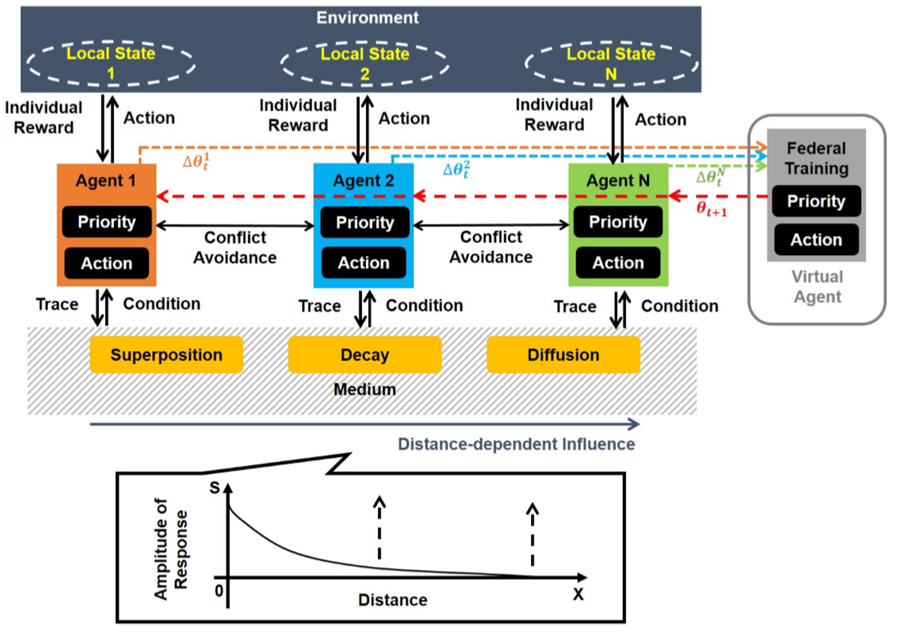
六、算法的智能体扩展

在真实智能体系统中，动态规划不仅能规划路径，还能：

1. 在强化学习中生成中间奖励（Subgoal Rewards）；

2. 在多智能体系统中进行任务分配（Task Allocation）；

3. 结合LLM（大语言模型）进行语义任务分解，例如：

   # 使用LLM将自然语言任务分解为结构化子任务
   from openai import OpenAI
   client = OpenAI()
   
   task = "制作咖啡并清理桌面"
   response = client.chat.completions.create(
       model="gpt-4o-mini",
       messages=[{"role": "user", "content": f"请将任务'{task}'分解为可执行的子目标列表"}]
   )
   print(response.choices[0].message.content)
   

   通过LLM生成语义级子目标，再结合动态规划确定执行顺序，实现“语义—规划”一体化的智能体架构。

七、总结与展望

本文介绍了基于动态规划的智能体任务分解算法，从理论到实战展示了如何：

• 建模子目标依赖；
• 利用DP计算最优子目标序列；
• 将算法扩展到语义级任务规划。

未来的智能体系统可将**大语言模型（LLM）+ 动态规划（DP）**相结合，形成“语义理解 + 最优任务分解”的混合智能体，为复杂多任务环境下的AI决策提供更高效与鲁棒的解决方案。

八、可扩展方向

未来的研究可探索：

• 结合**蒙特卡洛树搜索（MCTS）**提升动态环境鲁棒性；
• 将DP嵌入**层级强化学习（HRL）**框架；
• 在自主机器人与AI Agent协作系统中实现动态任务分配。

总结：智能体任务分解算法：基于动态规划的子目标生成策略

本文围绕智能体（Agent）在复杂任务场景下的任务分解问题展开，提出并实现了一种基于动态规划（Dynamic Programming, DP）的子目标生成策略。核心思想是通过“最优子结构”与“状态递推”机制，将整体任务划分为一系列可管理、可优化的子任务，从而实现全局最优的执行路径。

主要内容与结论如下：

1. 理论基础

   • 动态规划适用于智能体任务分解，因为它能处理子目标之间的依赖与重叠问题。
   • 状态定义为“已完成子任务集合”，转移方程通过最小化代价实现最优子目标选择。

2. 算法实现

   • 利用DP缓存机制避免重复计算，大幅提升效率。
   • 代码示例展示了从起始点出发访问多个子目标的最优路径求解，相当于TSP问题在智能体任务空间中的应用。

3. 智能体扩展性

   • 动态规划可嵌入强化学习（RL）框架，用于生成中间奖励（subgoal rewards）。
   • 结合大语言模型（LLM），可实现从自然语言任务到结构化子目标的自动生成。

4. 未来展望

   • 可将DP与蒙特卡洛树搜索（MCTS）、层级强化学习（HRL）融合，用于动态与多智能体任务环境。
   • LLM + DP 的混合智能体框架将成为未来AI自主规划系统的重要方向。

一句话总结：

基于动态规划的任务分解算法，为智能体提供了从全局最优角度生成子目标序列的能力，是构建自主、可解释、可优化AI决策系统的重要基石。