CSP-J基础之数学基础 矩阵基础 一篇搞懂
@TOC
前言
在CSP-J(全国青少年信息学奥林匹克联赛)基础阶段的学习中,数学基础是非常重要的一部分,其中矩阵是关键的概念之一。矩阵广泛应用于计算机科学、物理学、工程学等多个领域,特别是在图像处理、线性代数、算法优化等方向上。
学习矩阵不仅能帮助我们解决线性方程组,还为深入理解图论、机器学习等高级领域打下坚实的基础。本文将从矩阵的基础知识出发,帮助读者一步步掌握矩阵的定义、分类、运算(如加法、乘法、转置等),以及矩阵在解决线性方程组中的应用。通过这一篇文章,希望大家能全面掌握矩阵的基本理论与应用技巧,为CSP-J考试打下坚实的数学基础。
矩阵基本定义与类型
矩阵是一种用来整理和排列数字、物体或者数据的方式,就像我们把东西放在表格里一样。我们可以把矩阵看作一个“盒子”,这个盒子里面装着一堆数字,它们排成行和列。
-
一维矩阵:想象一排数字,就像你在纸上写了一串数。这叫做一维矩阵,比如 [1, 2, 3, 4, 5],它只有一行或者一列。
-
二维矩阵:这就像一个表格,里面有好几行和好几列数字。比如:

这里有两行三列,这是一个二维矩阵。
-
三维矩阵:想象一个盒子里装了好几个表格,每个表格像刚才的二维矩阵。这叫做三维矩阵。你可以把它想成一个立体的矩形,每层里面都有行和列。
矩阵的严格数学定义:
一个矩阵是一个由元素按照特定的行和列排列的二维数组。我们常用矩阵来表示线性代数中的向量、线性变换等。
一维矩阵(严格定义):
严格来说,一维矩阵可以被看作一个行向量或列向量。例如,一个 (1 \times n) 的矩阵表示一个行向量:
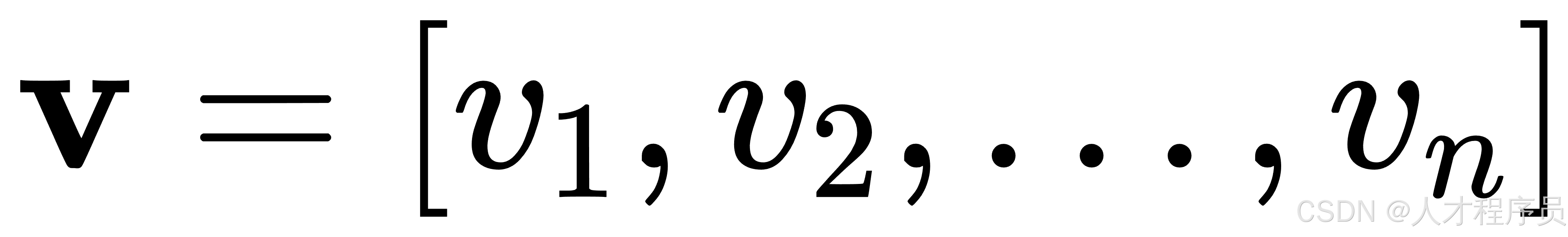
或一个
的矩阵表示一个列向量:
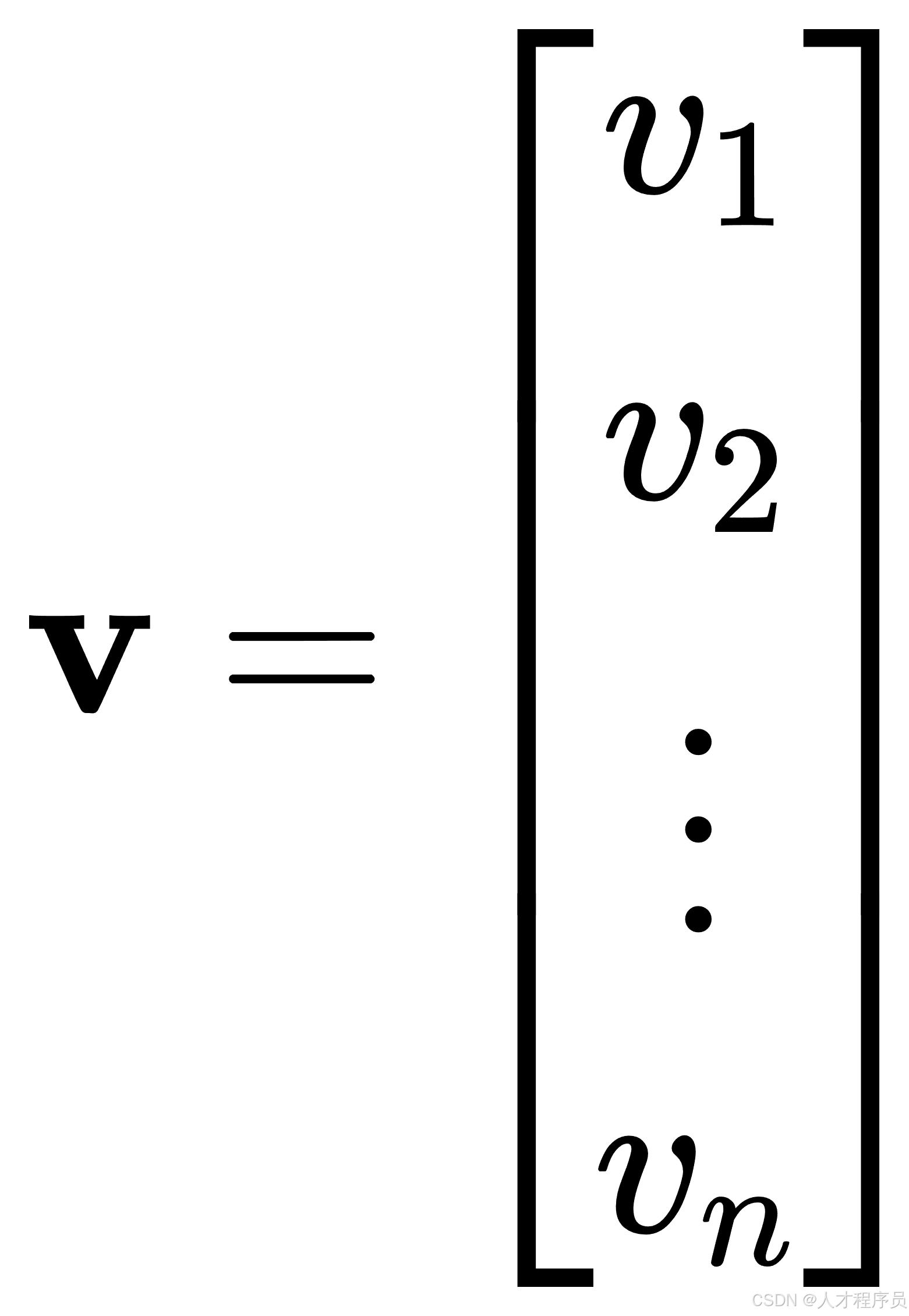
二维矩阵(严格定义):
一个二维矩阵是一个 m x n 的矩阵,由 (m) 行 (n) 列组成:
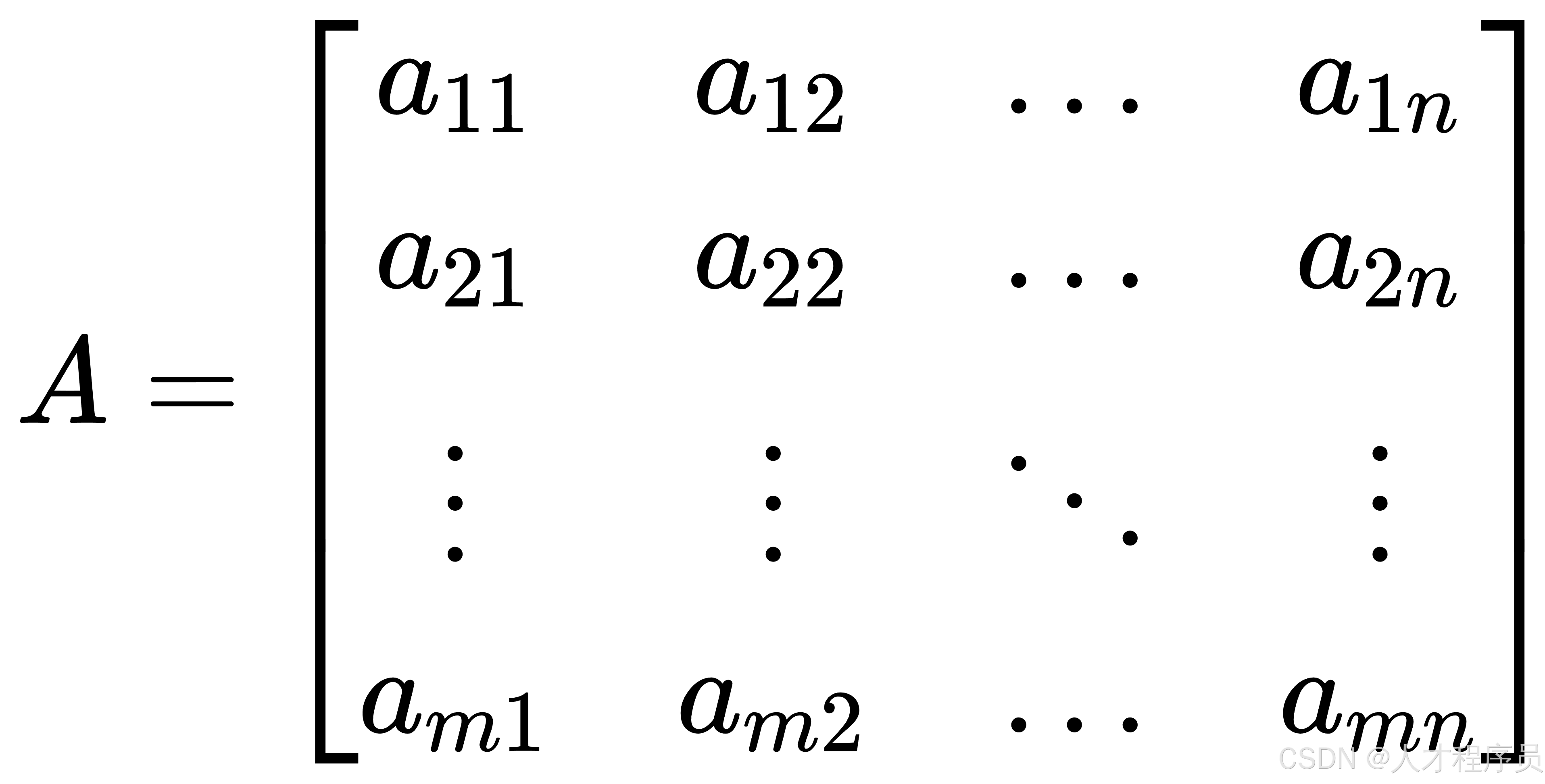
其中 
表示矩阵第 (i) 行第 (j) 列的元素。
三维矩阵(严格定义):
三维矩阵可以被看作是多个二维矩阵的堆叠。形式上,它可以表示为一个大小为 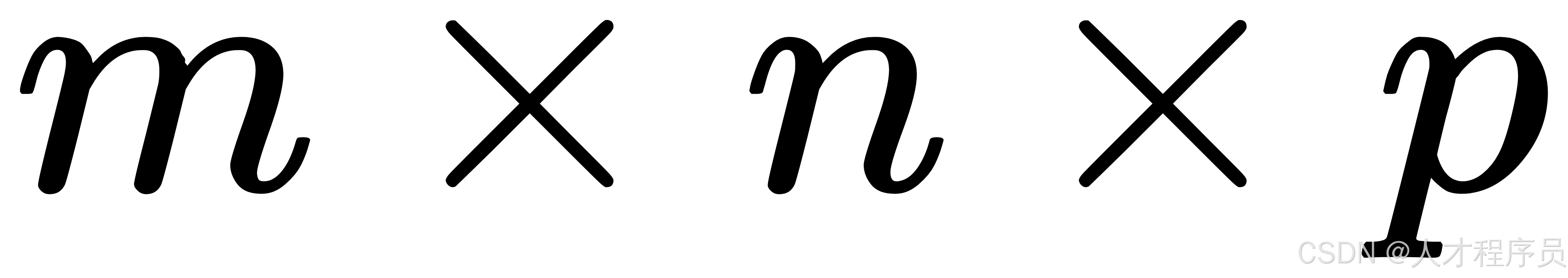
的张量(高维数组),其中每个元素可以标记为 (a_{ijk}),表示第 (i) 行,第 (j) 列,和第 (k) 个二维矩阵的元素。
矩阵在数学中用于表达线性映射、系统的线性方程、旋转变换等。
矩阵、方阵与列矩阵
矩阵,就像是一个“数字的表格”,你可以把它看作是把很多数字整齐地排成“行”和“列”。每个数字都有它自己的“位置”,像坐在表格里的小格子里一样。
-
矩阵:这个表格可以有很多行,也可以有很多列。比如:

这里有两行三列。
-
方阵:方阵就像是一个正方形的表格,它的行和列一样多,也就是说,有几行就有几列。比如:

这里有两行两列,所以它是一个方阵。
-
列矩阵:列矩阵是特别“瘦长”的表格,它只有一列,但有很多行。就像一个垂直排列的数字串,比如:

这里有四行但只有一列,所以它是一个列矩阵。
简单说,矩阵是一个“数字表格”,方阵是“行和列一样多”的表格,而列矩阵是“只有一列”的表格。
对角矩阵、比例矩阵与单位矩阵
-
对角矩阵:对角矩阵就像是一个特别的方阵,它的对角线上(从左上角到右下角)有数字,其他地方都是 0。你可以想象它像是一条斜斜的数字线,数字就在这条线上,比如:

在这里,数字 1、2 和 3 都在斜线(对角线)上,其他地方都是 0,这就是一个对角线矩阵。
-
比例矩阵:比例矩阵也是一种特殊的对角线矩阵,所有对角线上的数字都一样。想象你在对角线上放了同样的数字,而其他地方还是 0,比如:

这里对角线上的数字都是 5,其他地方是 0,这就是比例矩阵。就像每个数字都“按同样比例”放在对角线上一样。
-
单位矩阵:单位矩阵是非常特殊的比例矩阵,对角线上的数字全是 1,其他地方也是 0。它就像是“1 的专用方阵”,比如:

这个矩阵就是单位矩阵,对角线上全是 1,其他地方全是 0。单位矩阵就像数学里的“1”,它有很多重要的用途。
总结一下:
- 对角线矩阵:对角线上有数字,其他地方是 0。
- 比例矩阵:对角线上都是同样的数字,其他地方是 0。
- 单位矩阵:对角线上全是 1,其他地方全是 0。
三角矩阵与零矩阵
下三角矩阵与上三角矩阵
-
上三角矩阵:这个跟下三角矩阵刚好相反。想象一个方形的表格,如果你把表格的下半部分(对角线以下的部分)全都变成 0,只留下对角线及上方的数字,那就是一个上三角矩阵。就像表格的上半部分全是“实实在在”的数字,其他地方都是 0,比如:

这里对角线及上方的地方有数字,下面的地方都是 0。
-
下三角矩阵:想象一个方形的表格,如果你把表格的上半部分(对角线以上的部分)全都变成 0,只留下对角线及下方的数字,那就是一个下三角矩阵。就像表格的下半部分全是“实实在在”的数字,其他地方都是 0,比如:

这里对角线及下方的地方有数字,上面的地方都是 0。
零矩阵
-
零矩阵:零矩阵就是整个表格里全都是 0 的矩阵。它没有任何数字,只有 0,就像一个“全空”的表格,比如:

这里的所有位置都填满了 0,这就是零矩阵。
什么是矩阵转置?
矩阵转置(Matrix Transposition)就是把一个矩阵的行和列进行交换。换句话说,原本在第 (i) 行第 (j) 列的元素,经过转置后会出现在第 (j) 行第 (i) 列。
举个简单的例子:
假如我们有一个 (2 \times 3) 的矩阵:
1 2 3
4 5 6
这是一个有 2 行 3 列的矩阵。
它的转置矩阵会把行和列交换,变成一个 (3 \times 2) 的矩阵:
1 4
2 5
3 6
原本第一行变成了第一列,第二行变成了第二列。
矩阵转置的数学符号
在数学上,矩阵 (A) 的转置通常用符号 (A^T) 来表示,读作“(A) 的转置”。例如,矩阵:
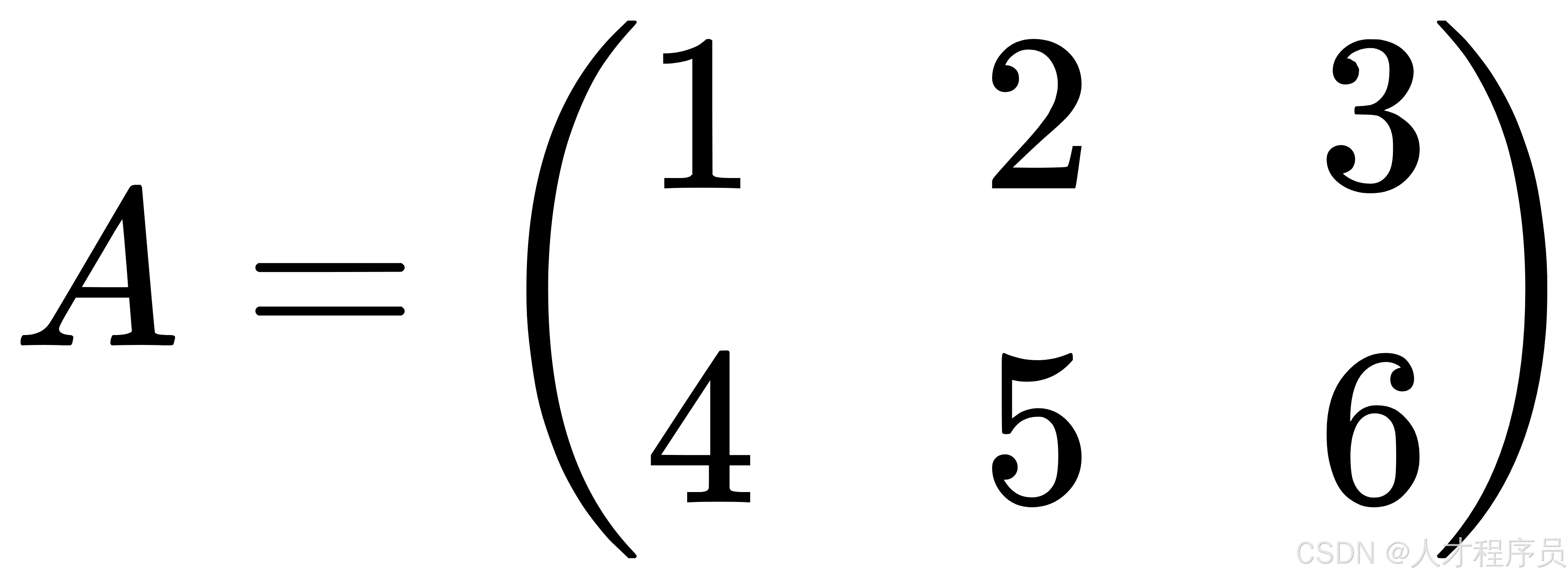
它的转置 (A^T) 是:
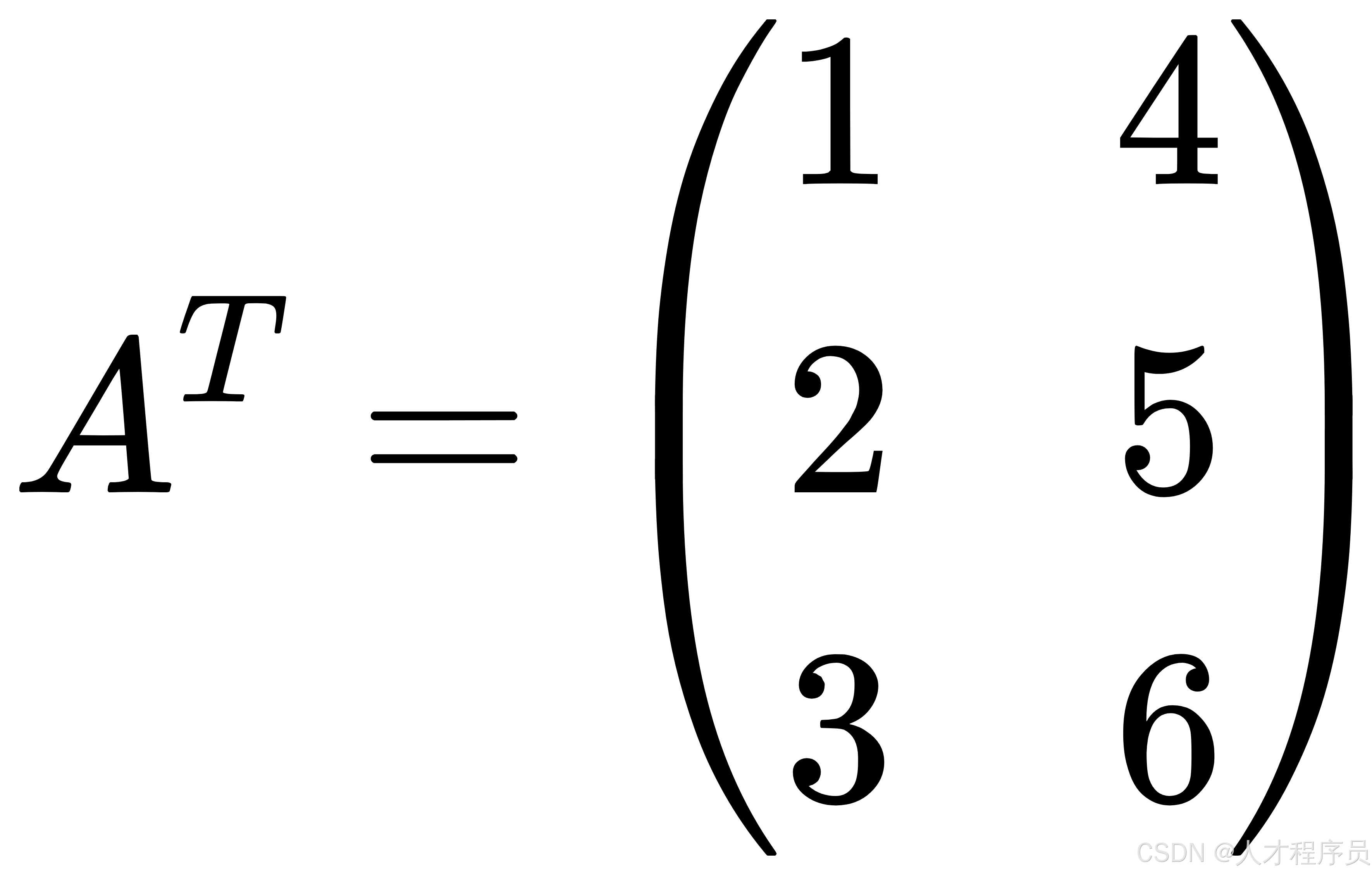
矩阵转置的步骤
- 原矩阵的第 1 行变成转置矩阵的第 1 列。
- 原矩阵的第 2 行变成转置矩阵的第 2 列,依此类推。
- 如果原矩阵是 m x t(即有 (m) 行和 (n) 列),那么转置后的矩阵就是 n x m 的矩阵(即有 (n) 行和 (m) 列)。
转置矩阵的性质
- 双重转置:一个矩阵转置两次,结果是原来的矩阵,即 ( (A^T)^T = A )。
- 加法的转置:两个矩阵相加后再转置,等于它们分别转置后再相加,即

。 - 乘法的转置:矩阵相乘后再转置,等于它们分别转置后,顺序颠倒地相乘,即

。
总结起来,矩阵转置是把矩阵的行和列互换,用 (A^T) 表示,转换步骤简单,且在计算中有重要的性质。
什么是矩阵的加法?
矩阵的加法就是把两个矩阵中相对应位置的元素进行相加,结果会得到一个新矩阵。注意,只有形状相同的矩阵才能相加,也就是说,两个矩阵必须有相同的行数和列数。
举个简单的例子:
如果有两个矩阵 ( A ) 和 ( B ),它们都是2 x 2 的矩阵(两行两列):
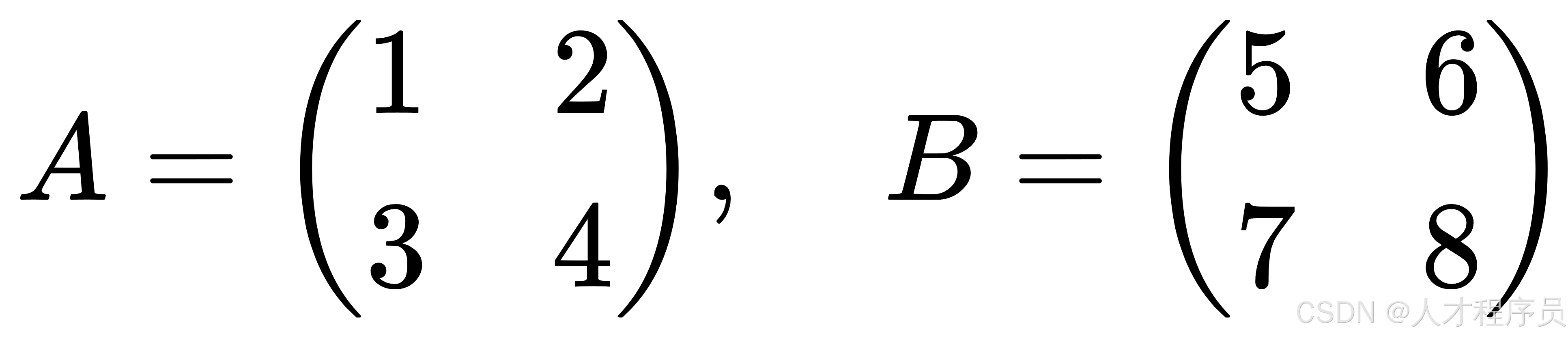
我们把两个矩阵的对应元素相加:
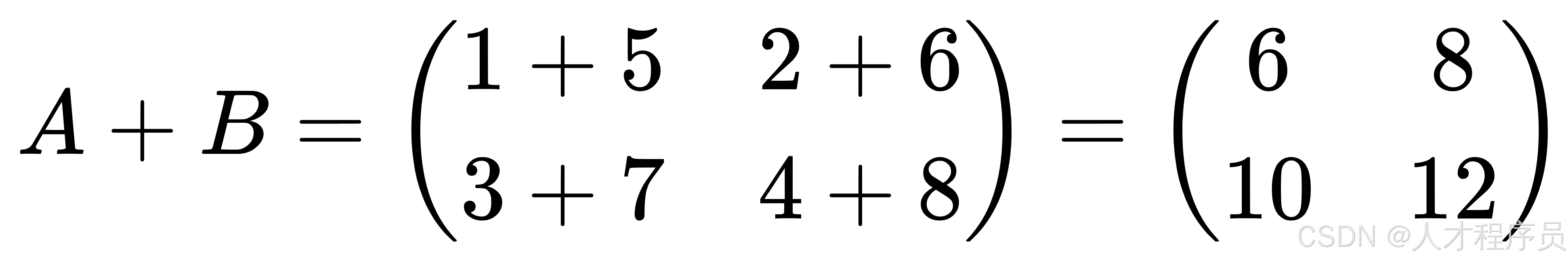
矩阵加法的规则:
- 对应元素相加:矩阵 (A) 和矩阵 (B) 的元素 (a_{ij}) 和 (b_{ij}) 相加,得到新矩阵 (C) 的元素 (c_{ij} = a_{ij} + b_{ij})。
- 相同的维度:矩阵加法要求两个矩阵的行数和列数必须相同。比如,两个 (3 \times 3) 的矩阵可以相加,而一个 (3 \times 3) 和一个 (2 \times 2) 的矩阵不能相加。
矩阵相加的条件:
- 两个矩阵必须形状相同。如果一个矩阵有 (m) 行 (n) 列,另一个矩阵也必须有 (m) 行 (n) 列,才能进行加法运算。
矩阵加法的数学符号:
如果有两个矩阵 (A) 和 (B),它们的维度都是 (m \times n),那么它们的和 (C = A + B) 也会是一个 (m \times n) 的矩阵,计算规则是:
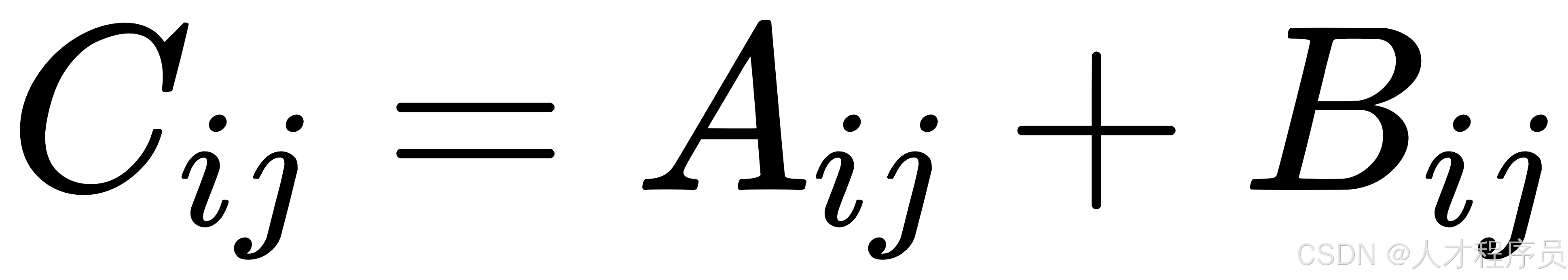
即:
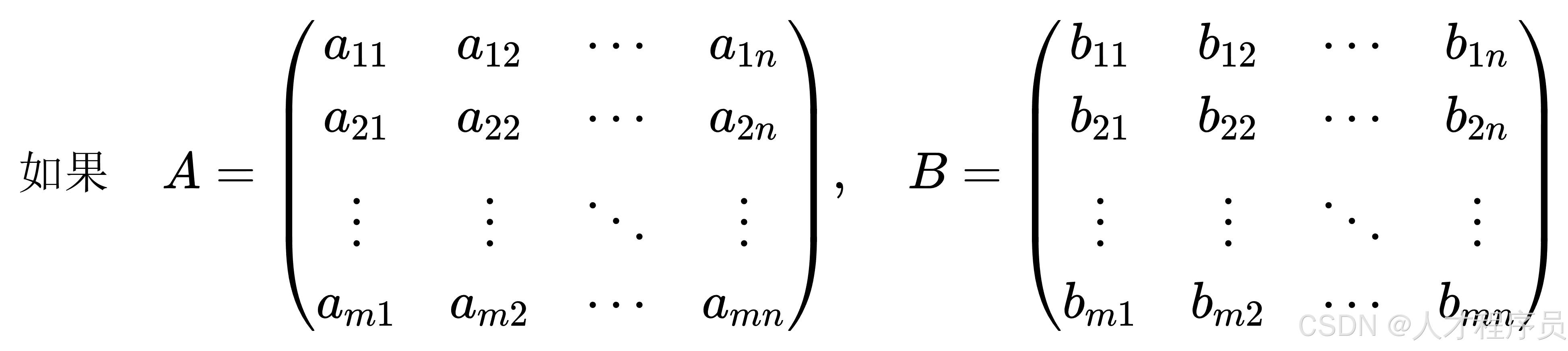
那么:
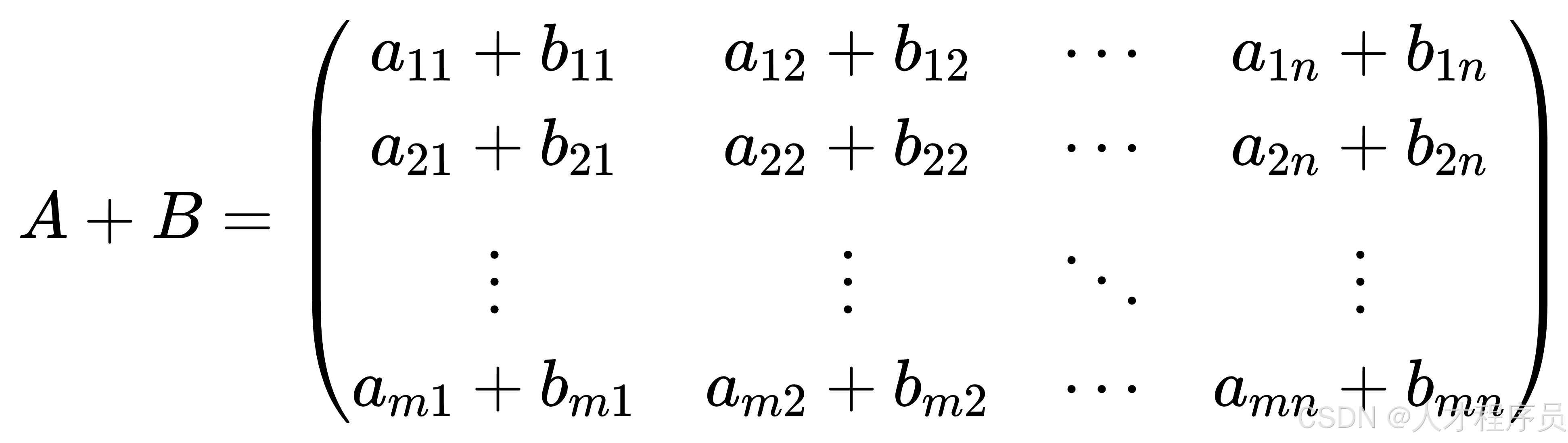
矩阵加法的性质:
- 交换律:矩阵加法满足交换律:( A + B = B + A )。
- 结合律:矩阵加法满足结合律:( (A + B) + C = A + (B + C) )。
- 零矩阵:矩阵与零矩阵相加时,结果是原矩阵:( A + 0 = A )。
总结来说,矩阵加法就是把两个相同大小的矩阵中对应位置的数字相加,得到一个新的矩阵。
什么是矩阵的标量乘法?
矩阵的标量乘法就是把矩阵中的每一个元素都乘以同一个数(标量),结果会得到一个新的矩阵。这是矩阵和标量之间的操作,而不是矩阵和矩阵之间的操作。
举个简单的例子:
假如我们有一个 2 x 2 的矩阵 ( A ) 和一个标量(比如 3):
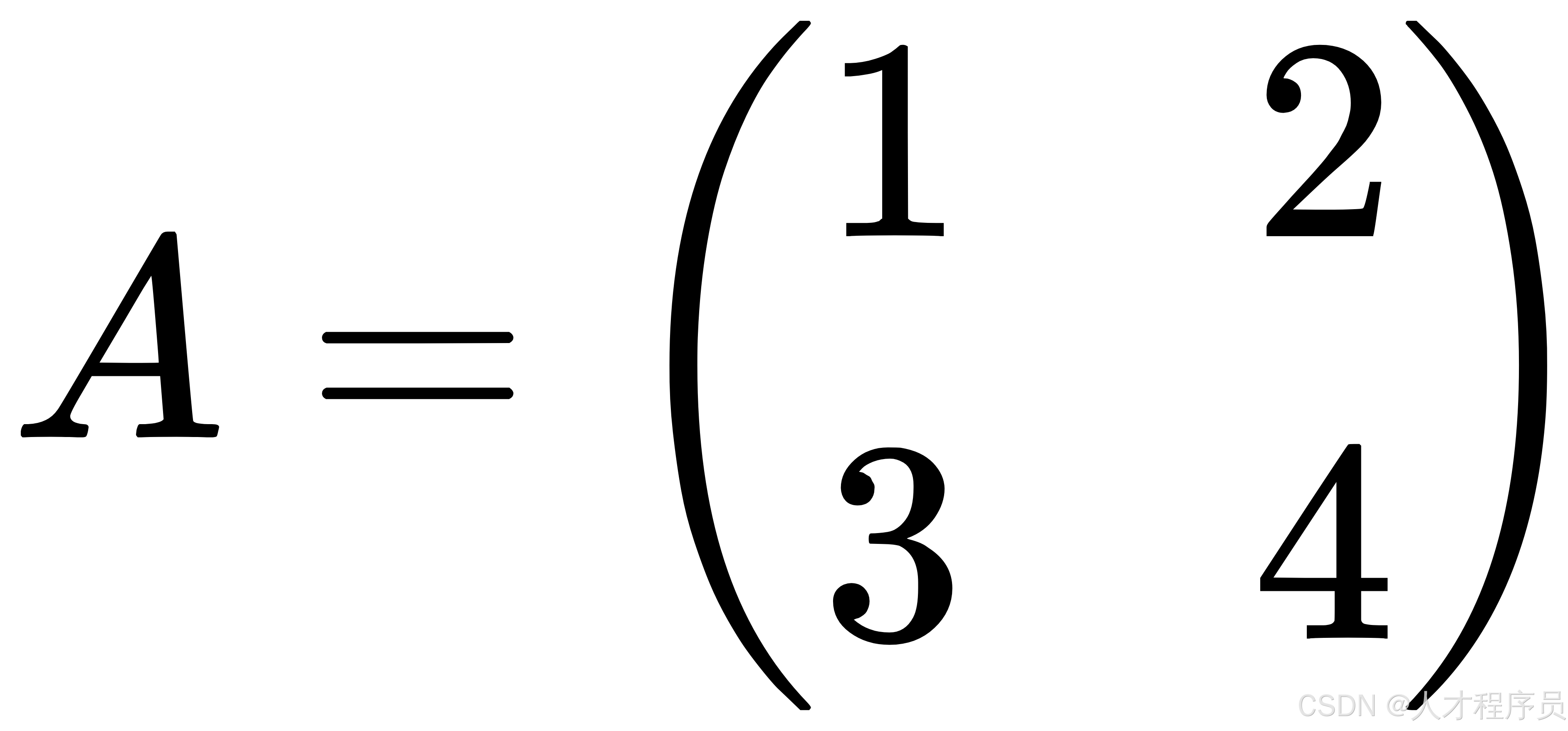
那么我们把矩阵 ( A ) 中的每个元素乘以 3,就得到一个新的矩阵:
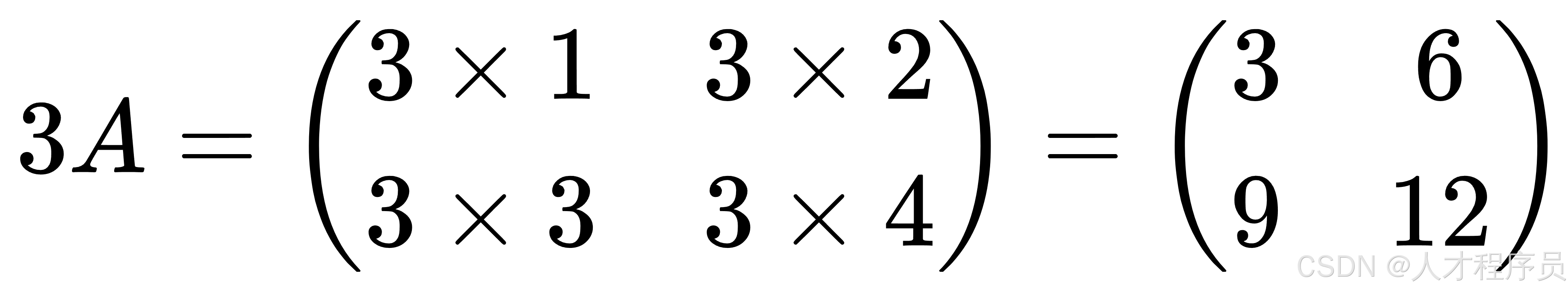
矩阵标量乘法的规则:
-
每个元素相乘:矩阵中的每个元素都乘以标量 ( k ),得到新的矩阵。

-
矩阵大小不变:标量乘法不会改变矩阵的行数和列数。
矩阵标量乘法的条件:
- 矩阵标量乘法没有限制,任何矩阵都可以与标量相乘。矩阵的维度(行数和列数)不变,只是矩阵中的每个数字都会乘以这个标量。
矩阵标量乘法的数学符号:
假设有一个标量 (k) 和一个 (m \times n) 的矩阵 (A),标量乘法 (k \cdot A) 的结果是一个 (m \times n) 的矩阵,每个元素 (A_{ij}) 都乘以标量 (k):
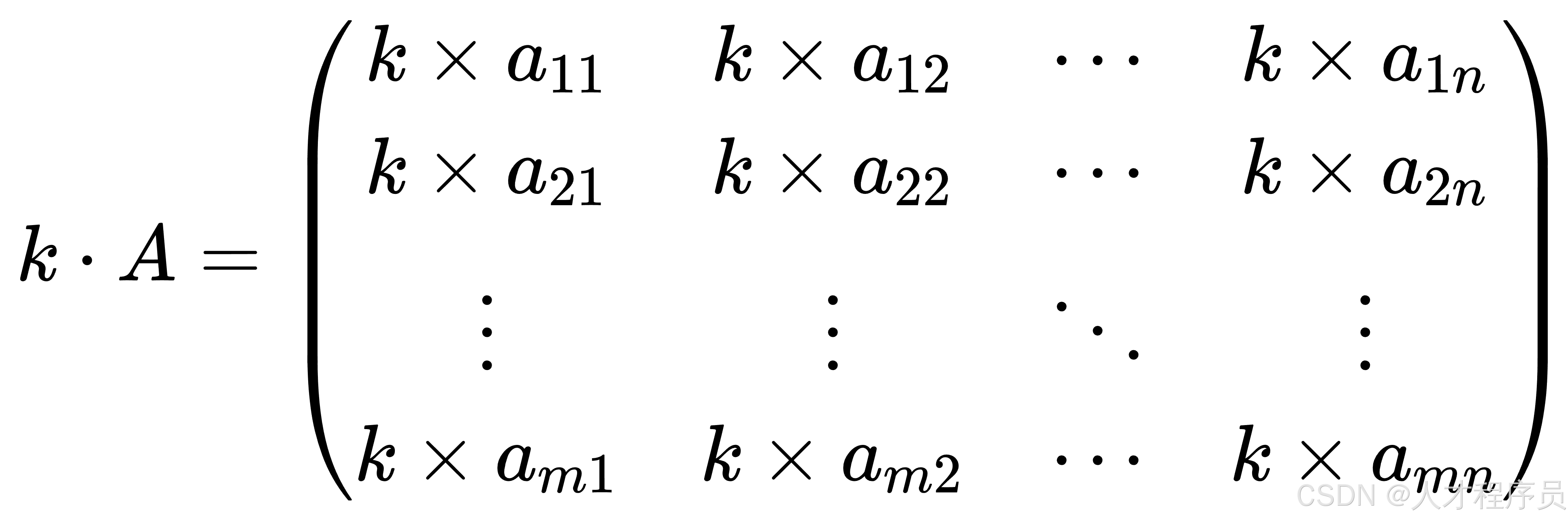
举个例子:
如果 ( A ) 是一个2 x 3的矩阵:
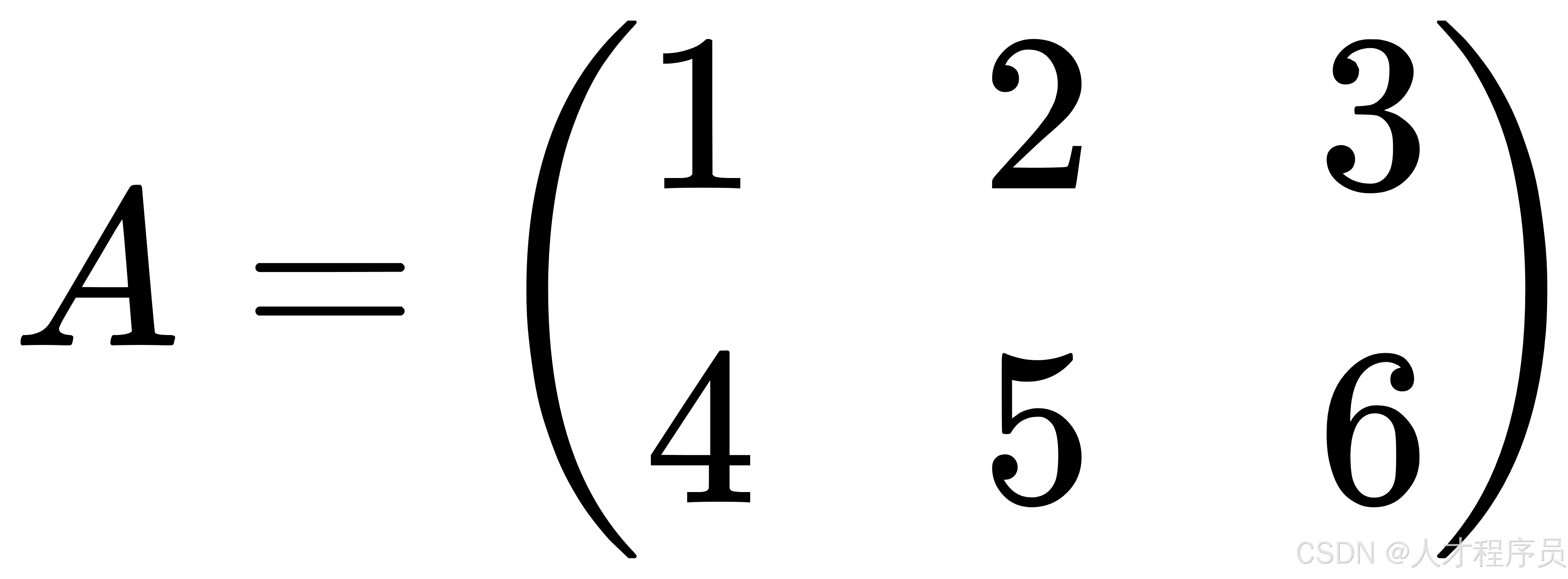
那么,标量乘以 2 的结果是:
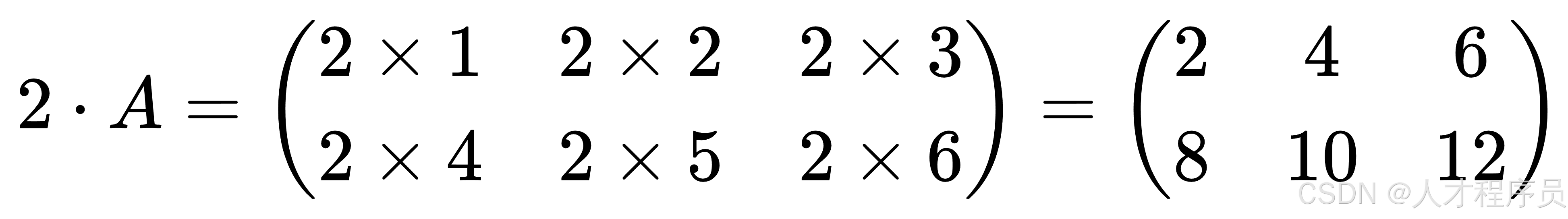
矩阵标量乘法的性质:
-
结合律:标量乘法满足结合律:

-
分配律:标量乘法对矩阵加法满足分配律:

-
单位标量:如果标量是 1,乘法结果不变:

。
总结:
矩阵的标量乘法是把一个数(标量)乘以矩阵中的每个元素,结果是一个新矩阵,维度不变。标量乘法可以帮助我们对矩阵进行比例放大或缩小等操作。
什么是矩阵的乘法?
矩阵的乘法是把一个矩阵和另一个矩阵相乘,并且乘法规则与我们平常的数字相乘不一样。它要求两个矩阵的列数与行数相匹配,然后通过行与列的对应元素相乘并求和来得到一个新的矩阵。
举个简单的例子:
假设有两个矩阵 ( A ) 和 ( B ),其中 ( A ) 是 2 x 3 的矩阵,而 ( B ) 是 3 x 2 的矩阵:
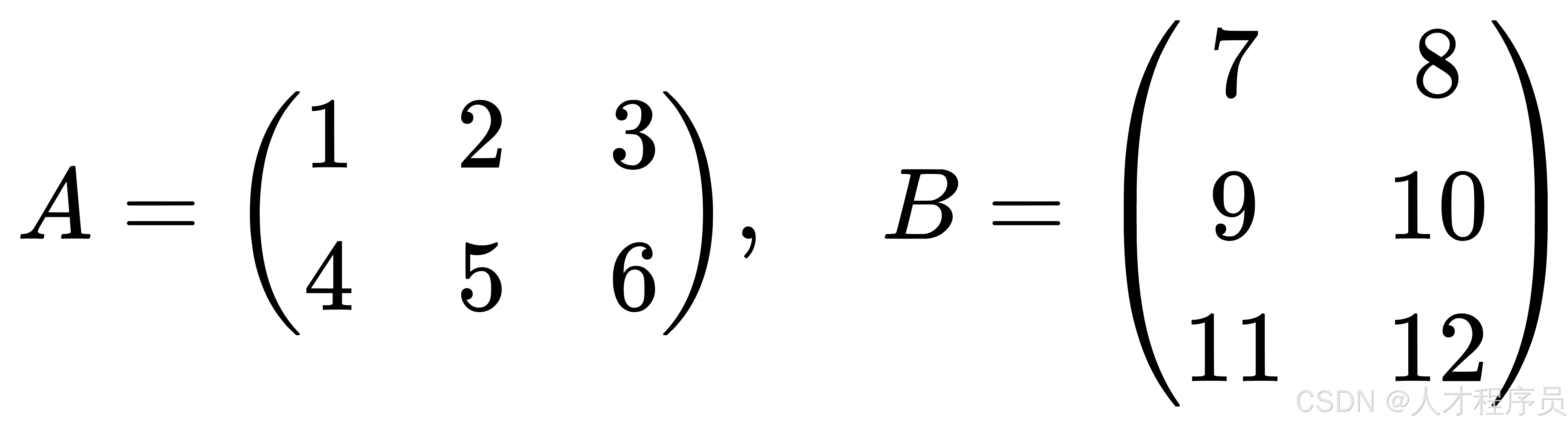
现在我们可以将矩阵 ( A ) 和矩阵 ( B ) 相乘:
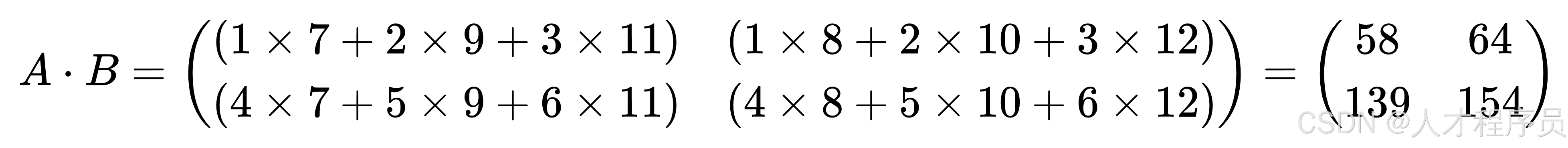
矩阵乘法的规则:
-
行列匹配:矩阵 ( A ) 的列数必须等于矩阵 ( B ) 的行数,只有这样它们才能相乘。假设 ( A ) 是 m x n 的矩阵,( B ) 是 n x p 的矩阵,那么它们的乘积 A x B 会是一个 n x p 的矩阵。
-
对应元素相乘并求和:矩阵乘法是把 ( A ) 的每一行与 ( B ) 的每一列对应元素相乘后再求和。
矩阵相乘的条件:
- 矩阵 ( A ) 的列数必须等于矩阵 ( B ) 的行数。只有在这种情况下,两个矩阵才能相乘。
矩阵乘法的数学符号:
如果 ( A ) 是一个 ( m \times n ) 的矩阵,( B ) 是一个 ( n \times p ) 的矩阵,那么它们的乘积 ( C = A \cdot B ) 是一个 ( m \times p ) 的矩阵。具体来说,矩阵 ( C ) 中第 ( i ) 行第 ( j ) 列的元素 ( C_{ij} ) 是由矩阵 ( A ) 的第 ( i ) 行与矩阵 ( B ) 的第 ( j ) 列对应元素相乘并求和得到的:
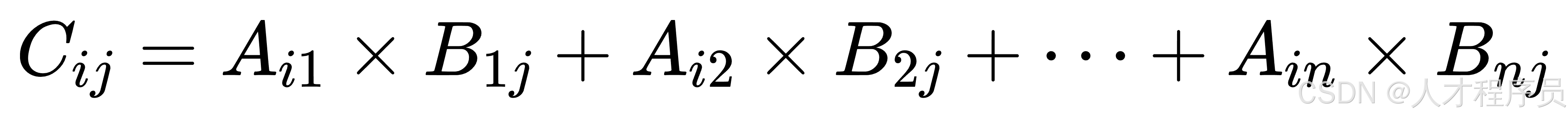
举个例子:
假设 ( A ) 是一个 ( 2 \times 3 ) 的矩阵:
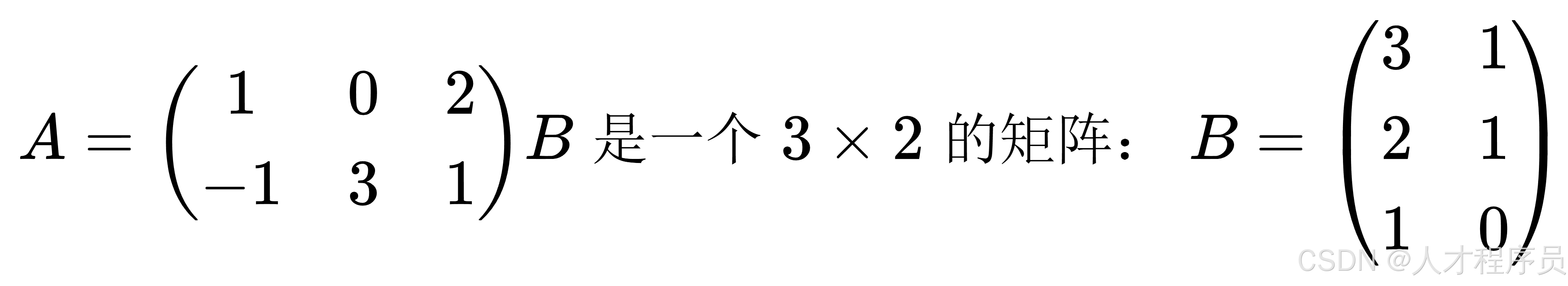
那么,矩阵 ( A ) 和矩阵 ( B ) 的乘积 A x B 是:
矩阵乘法的性质:
- 不满足交换律:矩阵乘法不满足交换律,也就是说

。 - 满足结合律:矩阵乘法满足结合律:

。 - 分配律:矩阵乘法对矩阵加法满足分配律:

。
矩阵相乘的注意事项:
- 矩阵维度的要求:两个矩阵能否相乘,取决于前一个矩阵的列数是否等于后一个矩阵的行数。
- 结果的矩阵大小:矩阵 ( A ) 和矩阵 ( B ) 相乘后,得到的结果矩阵的行数等于 ( A ) 的行数,列数等于 ( B ) 的列数。
总结:
矩阵的乘法并不是简单地把每个位置的元素相乘,而是通过行与列的乘积求和来得到一个新的矩阵。这个过程需要注意矩阵的维度匹配,只有当矩阵的列数与行数相同时才能相乘,且结果的维度由前一个矩阵的行数和后一个矩阵的列数决定。
矩阵与 C 语言数组的关系
在数学中,矩阵是一个由行和列组成的数字表,而在编程中,我们可以通过数组来表示矩阵。在 C 语言中,矩阵通常使用二维数组来存储。二维数组和矩阵有很多相似的地方,可以用它们来表示和操作矩阵。
C 语言中的数组:
在 C 语言中,数组是用来存储一组相同类型数据的结构。一个二维数组就是在一个普通数组的基础上增加了一个维度,可以理解为“数组的数组”,这与矩阵的行和列非常类似。
举个例子:
一个 ( 2 \times 3 ) 的矩阵 ( A ):
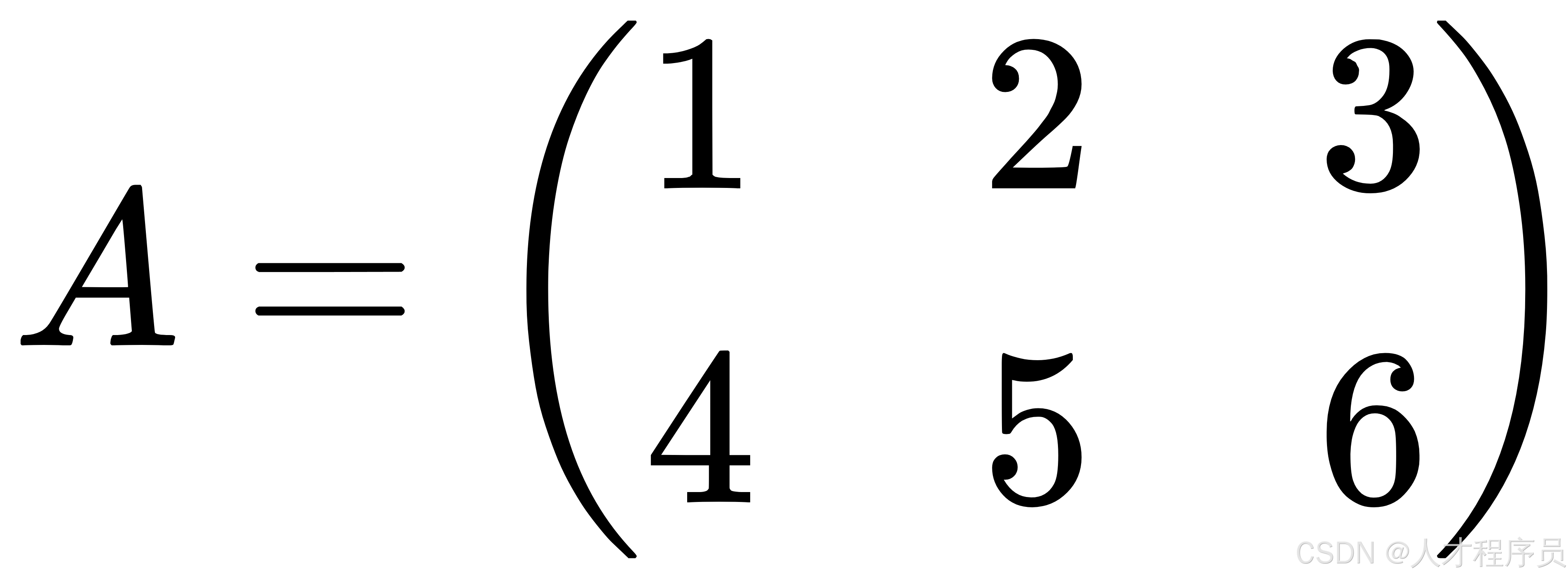
在 C 语言中可以用二维数组来表示:
int A[2][3] = {
{1, 2, 3},
{4, 5, 6}
};
A[2][3]表示一个包含 2 行和 3 列的二维数组。- 数组中的每个元素可以通过
A[i][j]访问,其中i是行号,j是列号。
矩阵和 C 数组的关系:
-
维度对应:在 C 中,矩阵的行和列可以用二维数组的第一维和第二维来表示。对于 (m \times n) 的矩阵,C 语言数组的声明是
A[m][n]。 -
访问矩阵元素:在 C 语言中,矩阵的第 (i) 行第 (j) 列的元素可以通过
A[i][j]访问,就像数学上的矩阵表示 (A_{ij}) 一样。 -
初始化:矩阵的元素可以通过数组初始化一次性赋值,如:
int A[2][3] = { {1, 2, 3}, {4, 5, 6} };这就像数学中矩阵的初始化一样。
-
存储方式:C 语言中的二维数组是按照行优先顺序存储的,意味着数组的所有元素会连续存放在内存中,先按行存放,再按列。例如,数组
A[2][3]实际在内存中的顺序是A[0][0], A[0][1], A[0][2], A[1][0], A[1][1], A[1][2]。 -
矩阵操作与数组操作:矩阵的基本操作,比如矩阵加法、标量乘法和矩阵乘法,可以通过二维数组中的元素进行相应的操作。例如,对应矩阵相加,C 语言中可以用嵌套的
for循环逐元素相加。
C 数组与矩阵的差异:
-
内存连续性:C 语言中的数组是内存中连续分配的,而数学上矩阵只是一种表示方式,不涉及具体的内存布局。
-
维度的灵活性:C 语言数组有固定的维度(必须在声明时确定),而数学上的矩阵可以任意大小。而在 C 语言中,如果需要更灵活的矩阵表示,可以使用动态内存分配(
malloc和free)来创建任意大小的矩阵。
矩阵与 C 数组之间的操作:
矩阵中的各种运算(如加法、乘法、转置等)可以通过对 C 语言二维数组的操作来实现。以下是矩阵乘法的简单实现:
矩阵乘法示例(C 代码):
#include <stdio.h>
void matrixMultiply(int A[2][3], int B[3][2], int C[2][2]) {
// 遍历 A 的行和 B 的列
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
C[i][j] = 0; // 初始化 C 的元素
for (int k = 0; k < 3; k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
}
int main() {
int A[2][3] = {{1, 2, 3}, {4, 5, 6}};
int B[3][2] = {{7, 8}, {9, 10}, {11, 12}};
int C[2][2];
matrixMultiply(A, B, C);
// 输出结果矩阵 C
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
printf("%d ", C[i][j]);
}
printf("\n");
}
return 0;
}
在上面的代码中,matrixMultiply 函数用 C 语言的二维数组来实现矩阵乘法,最终计算得到的矩阵结果会被存储在数组 C 中。
总结:
- 矩阵和 C 数组之间的关系非常紧密,C 语言的二维数组可以用来表示数学中的矩阵。
- 可以通过二维数组中的元素来实现矩阵的各种操作,比如矩阵的加法、乘法、转置等。
- C 数组的内存分配方式和矩阵存储有差异,但在实际编程中,通过适当的算法,我们可以轻松在 C 语言中实现各种矩阵操作。
矩阵与方程组的关系
在数学中,线性方程组是由多个线性方程组成的一组方程,它的解通常是多个变量的值。矩阵和方程组之间有非常紧密的联系,特别是在解决线性方程组时,矩阵可以用来简化方程的表示和运算。
什么是线性方程组?
一个线性方程组就是多个方程组成的系统,例如:
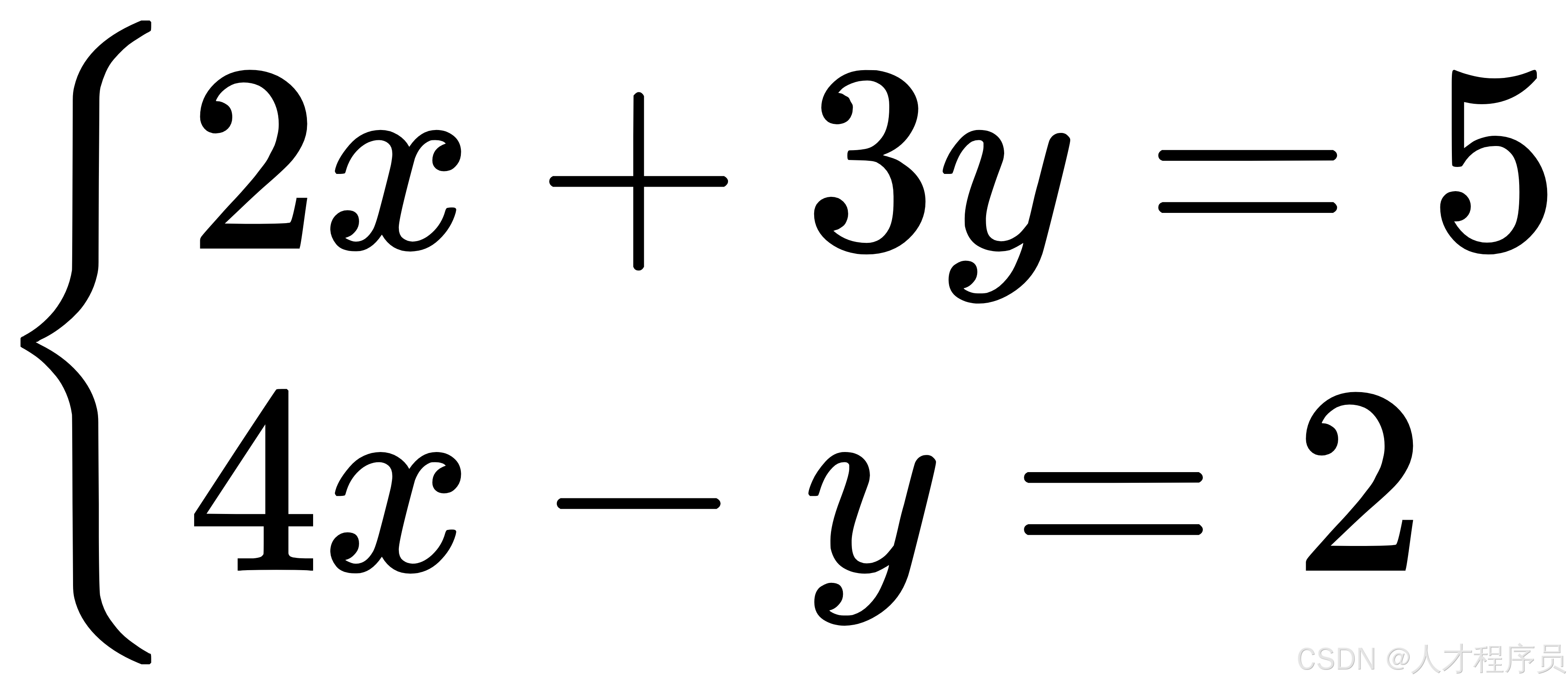
这是一个有两个变量 (x) 和 (y) 的线性方程组。我们需要找到 (x) 和 (y) 的值,使得两个方程同时成立。
矩阵表示法:
我们可以使用矩阵来表示这个方程组。线性方程组可以通过矩阵表示成矩阵乘法的形式:
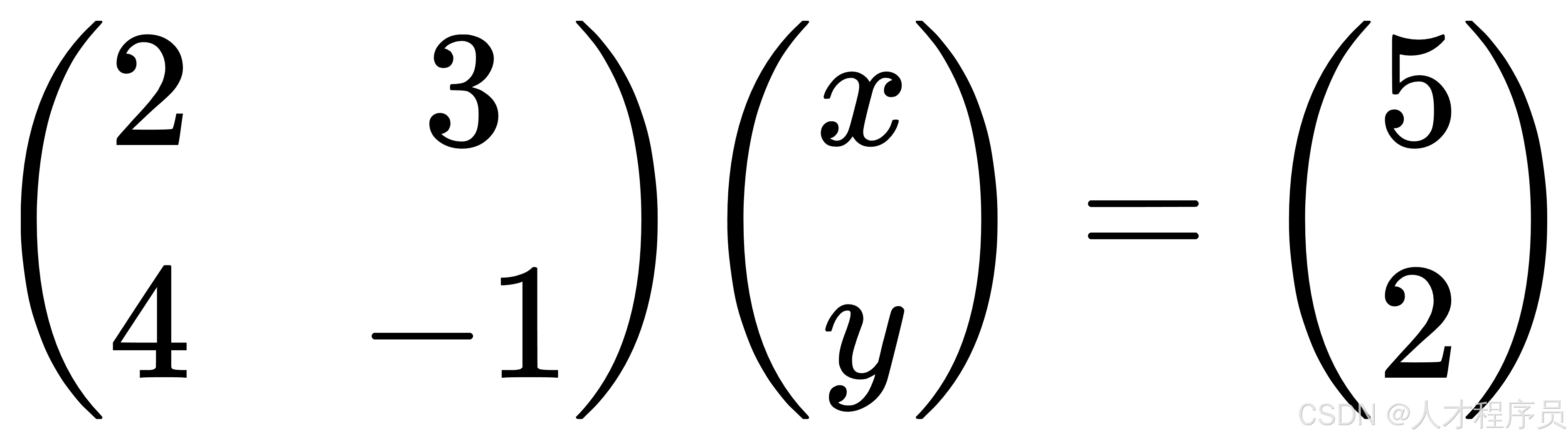
- 左边的矩阵是系数矩阵,每个元素对应方程组中变量的系数。
- 中间的矩阵是未知数矩阵,包含我们要求解的变量 (x) 和 (y)。
- 右边的矩阵是常数矩阵,表示方程组等号右边的常数。
这个矩阵表示法对应的方程可以写为:
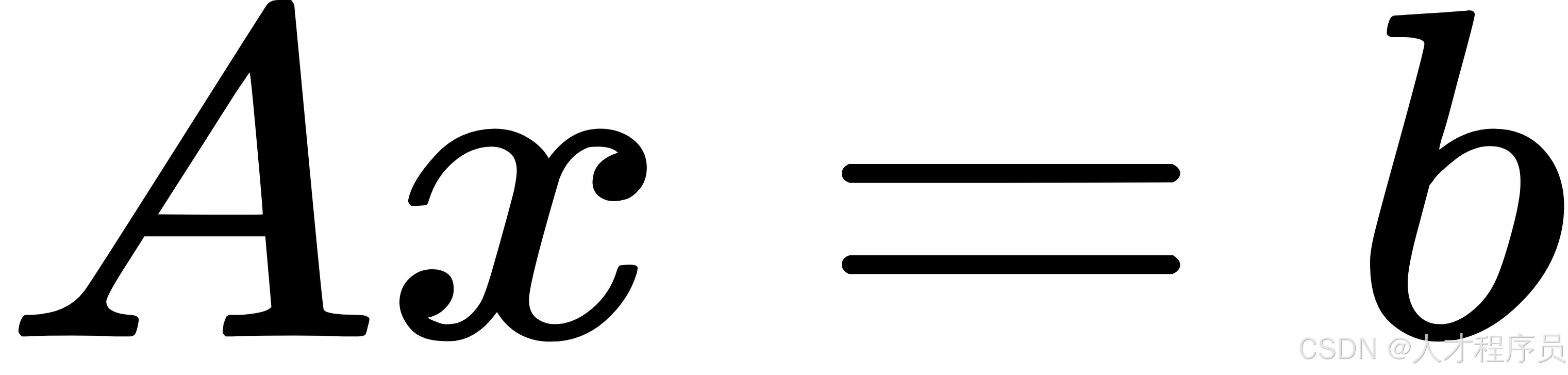
其中:
- ( A ) 是系数矩阵(例如 2 x 2 矩阵)。
- ( x ) 是未知数矩阵(包含 (x) 和 (y))。
- ( b ) 是常数矩阵(方程右边的常数项)。
矩阵与方程组的联系:
-
简化表示:使用矩阵表示线性方程组,使得整个系统简洁而有条理。在手写多元方程时,矩阵表示更方便理解和处理。
-
求解方法:我们可以通过矩阵的方法来解线性方程组。常见的方法包括:
- 逆矩阵法:如果矩阵 (A) 是可逆的,那么线性方程组的解可以表示为 (x = A^{-1}b),即通过求矩阵 (A) 的逆矩阵,然后用它乘以常数矩阵 (b) 得到解。
- 高斯消元法:通过对矩阵进行行操作,把方程组化为简化形式,得到解。
- Cramer法则:使用矩阵的行列式来解方程组。
矩阵与线性方程组的关系实例:
假设我们有以下线性方程组:
这个方程组可以用矩阵表示为:
这里:
- 系数矩阵 (A) 是 3 x 3的矩阵。
- 未知数矩阵 包含变量 (x, y, z)。
- 常数矩阵 包含方程组右边的常数 (6, -4, 27)。
我们可以使用不同的矩阵方法来求解这个方程组。
总结:
- 矩阵提供了一种简洁的表示方法,可以将复杂的线性方程组表示为矩阵乘法的形式。
- 通过矩阵的运算,可以有效地解决线性方程组。
- 矩阵运算可以通过许多方法,比如逆矩阵法、高斯消元法和Cramer法则等,来求解线性方程组的解。
逆矩阵是什么?
在矩阵运算中,逆矩阵与单位矩阵的概念非常相关。对于一个方阵(即行数等于列数的矩阵) (A),如果存在另一个矩阵 (A^{-1}),使得它与 (A) 相乘的结果是单位矩阵 (I),我们就称这个矩阵 (A^{-1}) 为 (A) 的逆矩阵。
数学表达式为:

- (I) 是单位矩阵,单位矩阵的特点是它的对角线元素都是 1,其他元素都是 0。例如,2×2 的单位矩阵是:
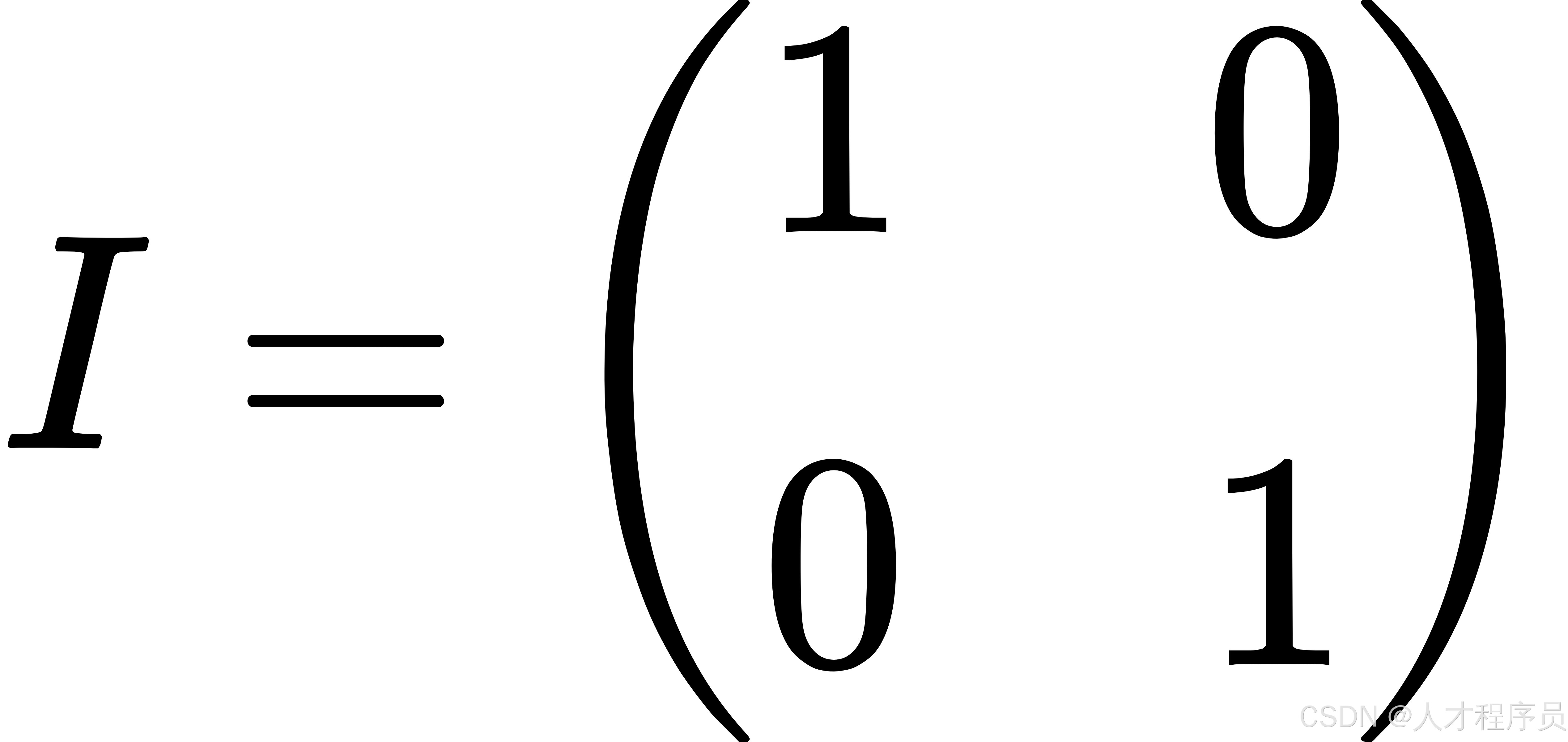
- 只有可逆矩阵才有逆矩阵。如果一个矩阵的行列式不为 0,则它是可逆的。
如何求逆矩阵?
对于一个 (n \times n) 的方阵 (A),逆矩阵 (A^{-1}) 的求法可以通过以下几种方法实现:
-
高斯消元法:通过对矩阵进行初等行变换(即对矩阵的行进行加减、交换或乘除),把原矩阵 (A) 转化为单位矩阵 (I),并对单位矩阵进行相同操作,最终结果就是 (A^{-1})。
-
伴随矩阵法(适用于较小规模矩阵):对于 2×2 或 3×3 的矩阵,可以通过计算伴随矩阵和矩阵的行列式来求逆矩阵。
- 对于一个 2×2 矩阵 (A):

其中 (ad - bc) 是矩阵 (A) 的行列式,行列式不为零时矩阵可逆。
使用逆矩阵求解线性方程组
线性方程组可以用矩阵的形式表示为 (Ax = b),其中:
- (A) 是系数矩阵,
- (x) 是包含未知数的列向量(解向量),
- (b) 是常数矩阵(常数向量)。
若矩阵 (A) 可逆,我们可以通过逆矩阵法来解方程组。其步骤如下:
- 先将方程 (Ax = b) 左乘矩阵 (A^{-1}):
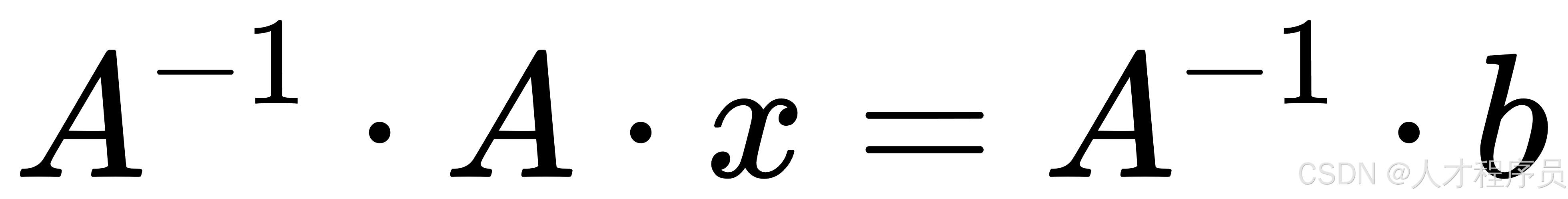
- 由于 (A^{-1} \cdot A = I)(单位矩阵),方程简化为:
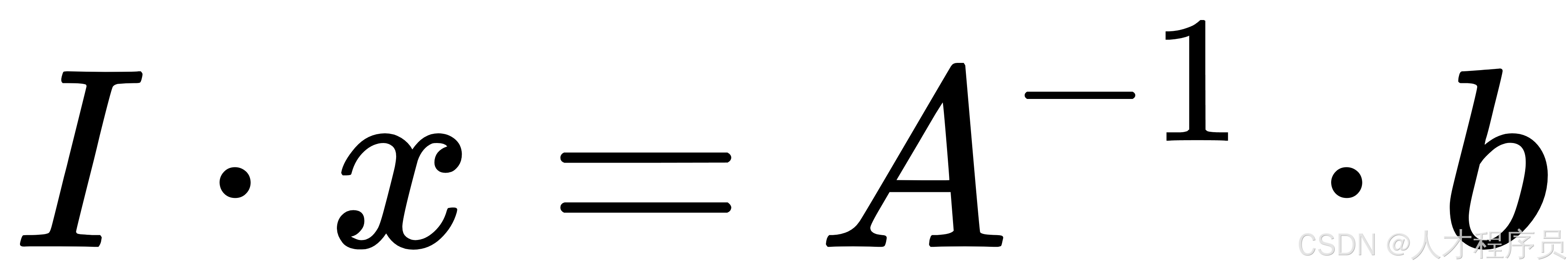
- 因为单位矩阵乘以任意向量还是该向量本身,因此得到:
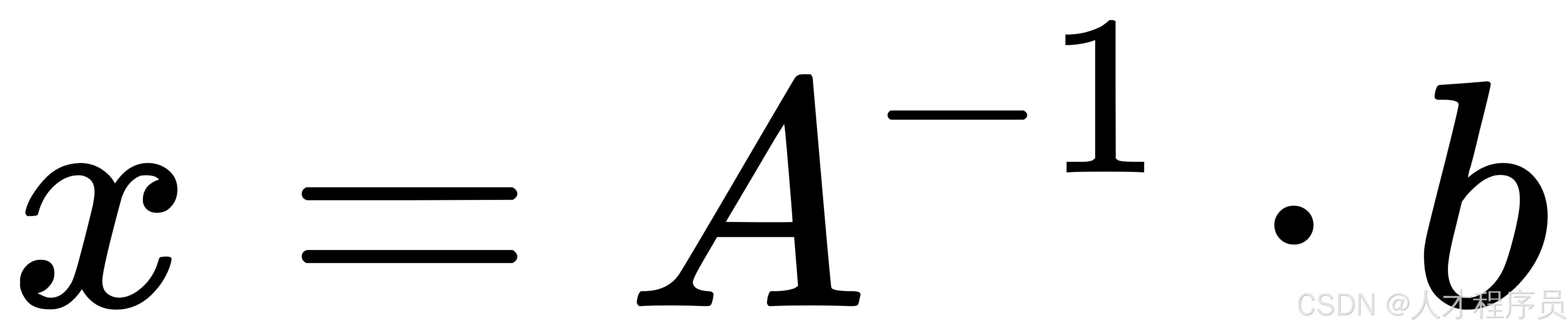
通过计算 (A^{-1}) 并乘以 (b),就可以求得线性方程组的解 (x)。
逆矩阵求解线性方程的例子:
假设我们有以下线性方程组:
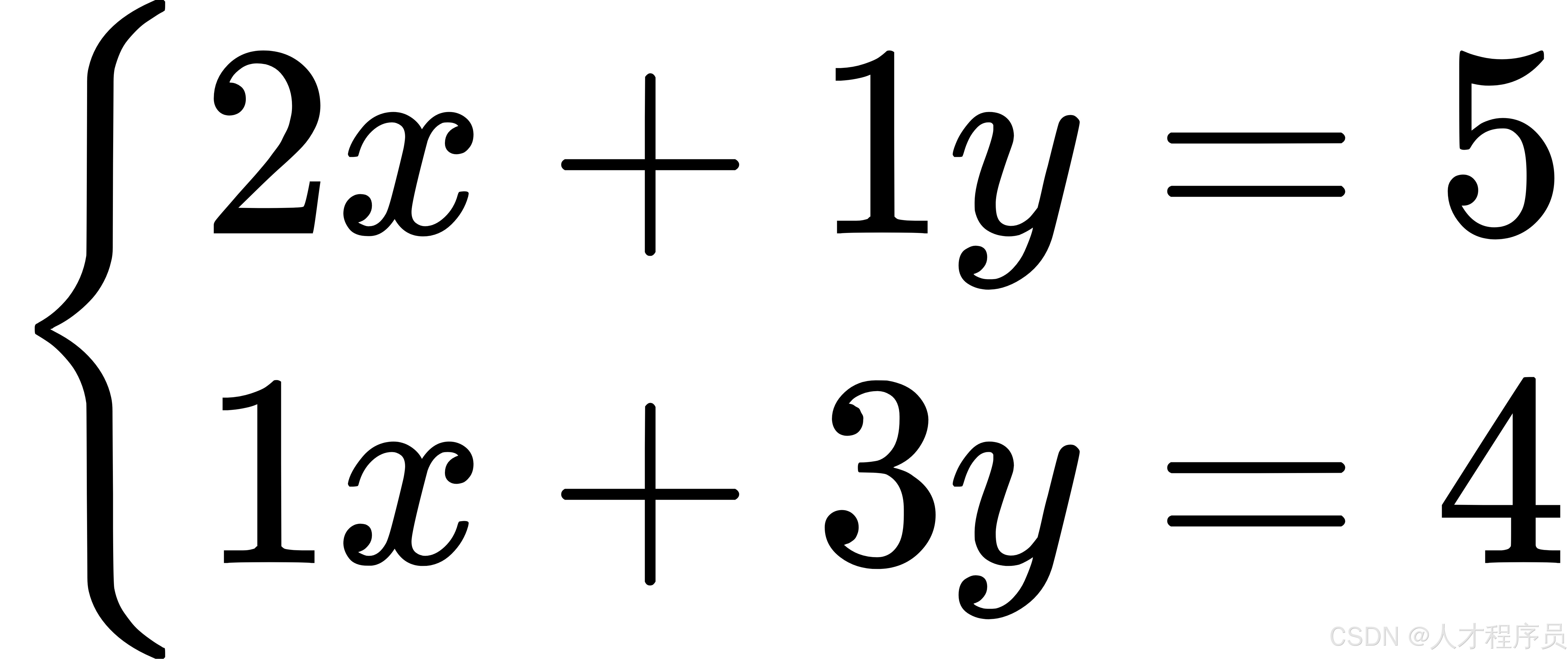
对应的矩阵表示为:
我们称系数矩阵为 (A),解向量为 (x),常数向量为 (b):
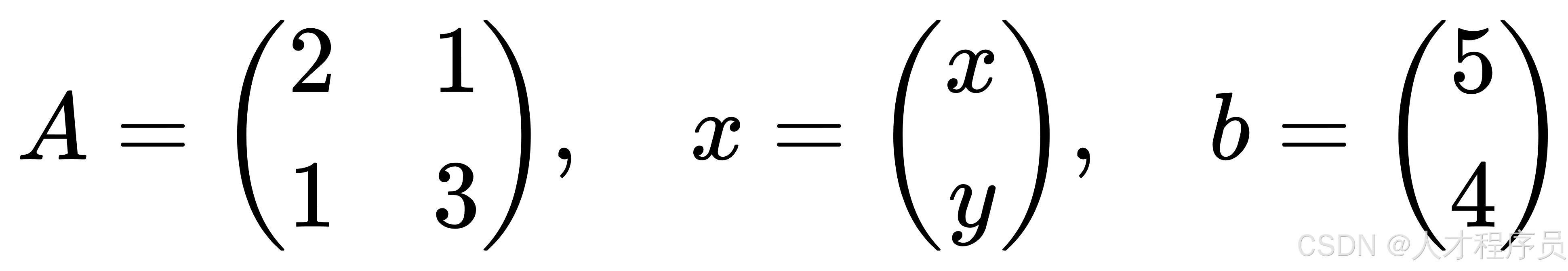
为了求解这个方程组,我们先求出 (A) 的逆矩阵 (A^{-1})。
通过公式:
然后将 (A^{-1}) 与 (b) 相乘,求出解 (x):
因此,解 (x) 和 (y) 分别为:
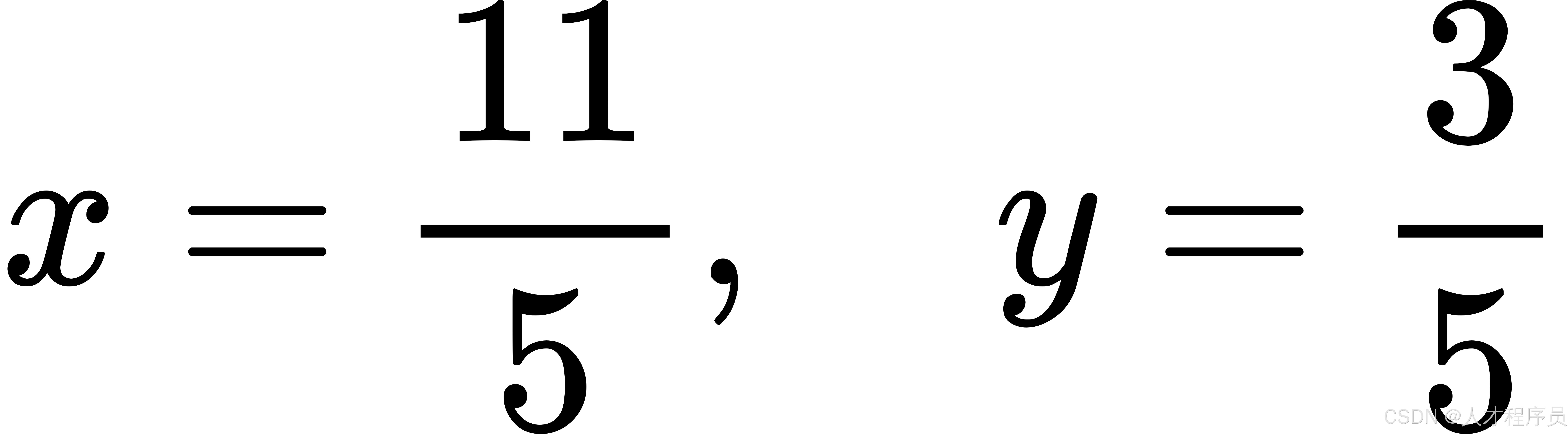
总结
- 逆矩阵 是一个与原矩阵相乘得到单位矩阵的矩阵。
- 当我们使用逆矩阵求解线性方程组时,首先要确定矩阵是可逆的,然后通过求逆矩阵来解方程。
- 逆矩阵法可以简化解线性方程组的过程,特别是对于系数矩阵可逆的情况,可以快速得出解。
总结
通过本篇文章的学习,大家应当已经对矩阵的基本概念和操作有了全面的理解,包括:
矩阵的定义及其各种分类,如方阵、零矩阵、单位矩阵等。
常见的矩阵运算,如加法、标量乘法、矩阵乘法及转置。
如何使用矩阵解决线性方程组,特别是逆矩阵法在求解线性方程组中的应用。
掌握这些内容不仅对应付CSP-J考试大有帮助,更能为日后的学习打下坚实的数学和编程基础。在实际编程中,矩阵运算常被应用于图像处理、图论算法、机器学习等领域。因此,扎实的矩阵知识不仅限于竞赛,还将伴随大家在更高层次的数学和计算机应用中发挥重要作用。
通过这篇文章的学习,相信大家能够对矩阵基础有深刻的理解,并能在CSP-J的比赛中更好地应用这些知识。
- 点赞
- 收藏
- 关注作者

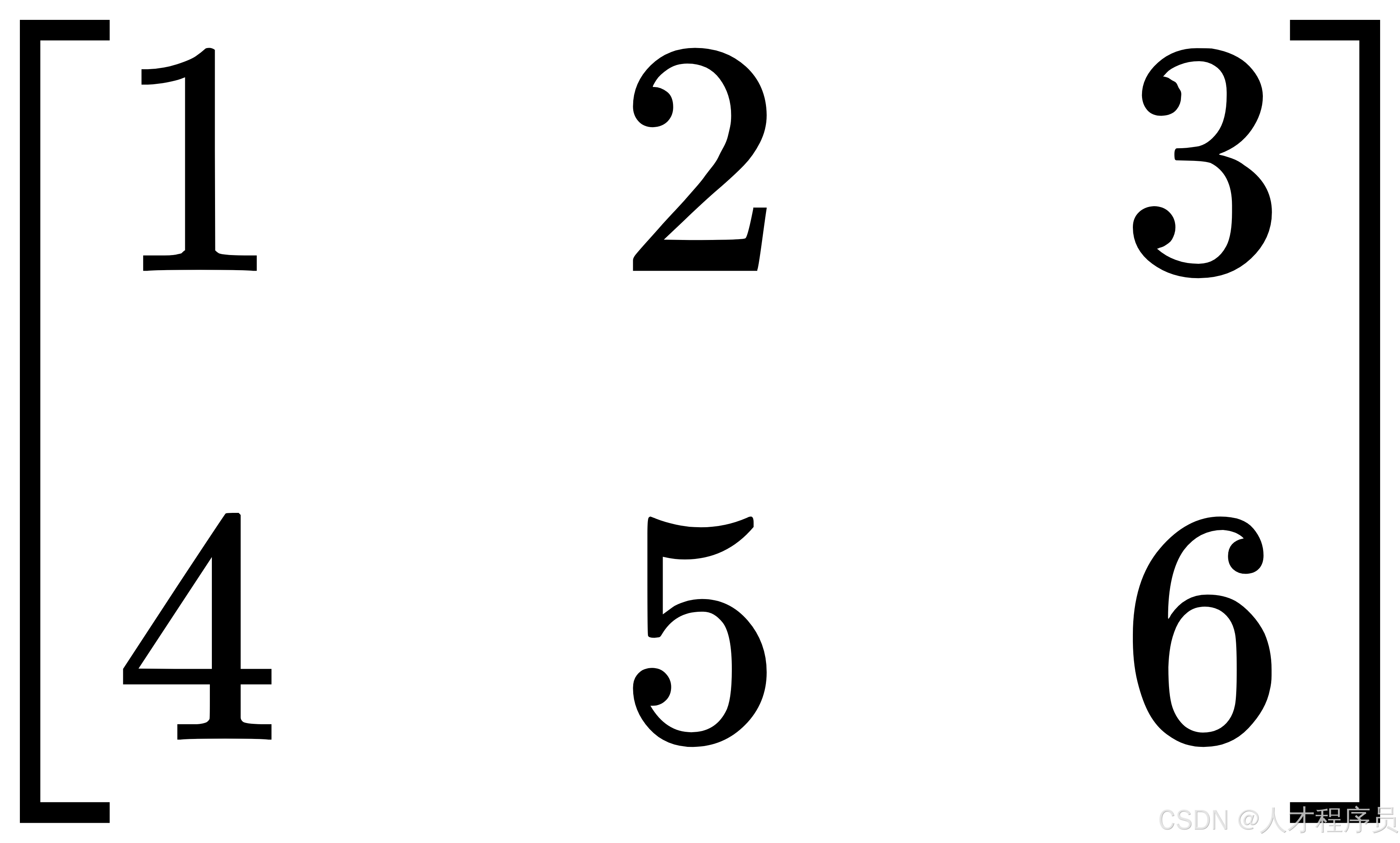
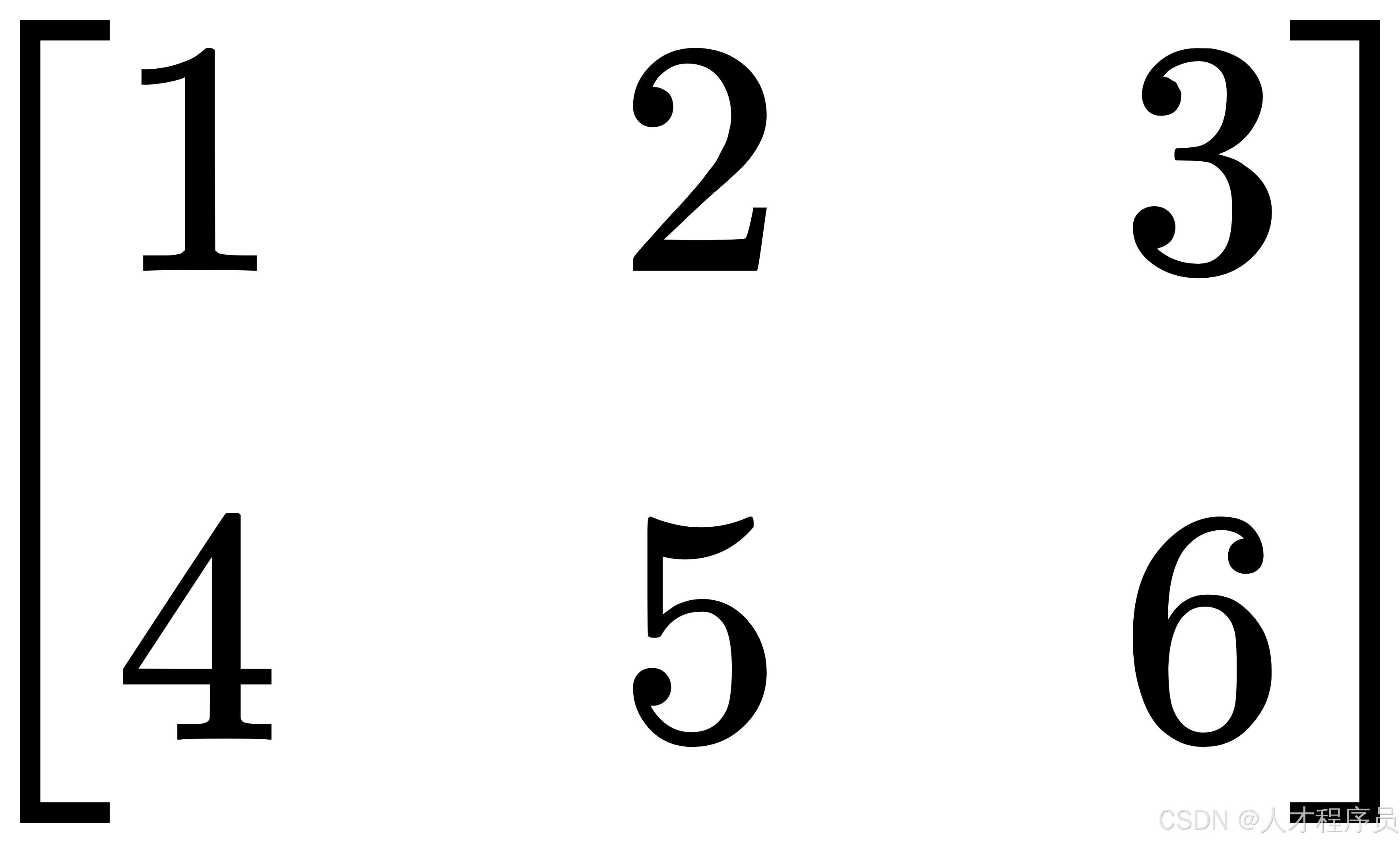








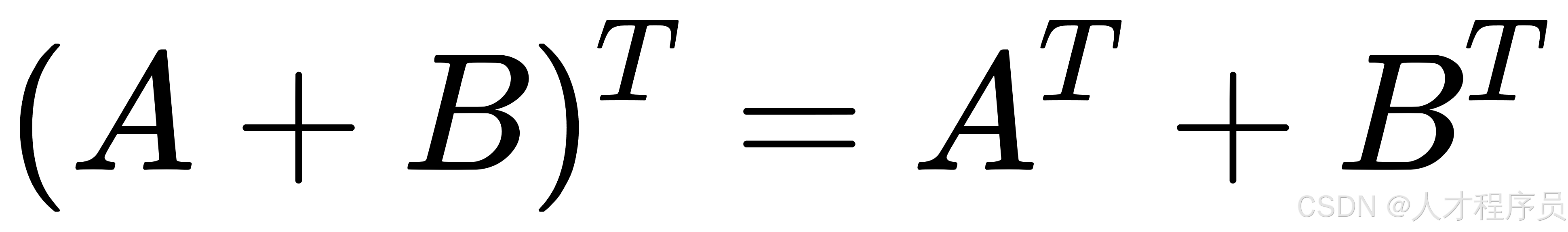
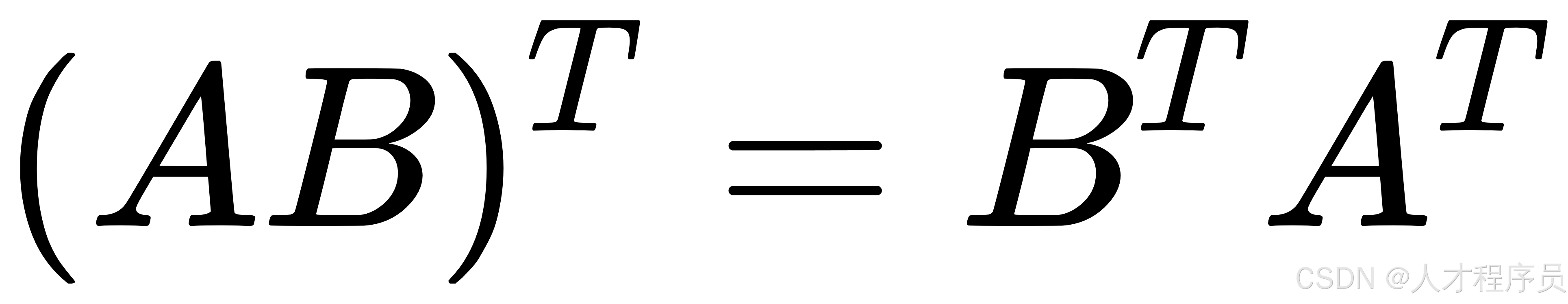
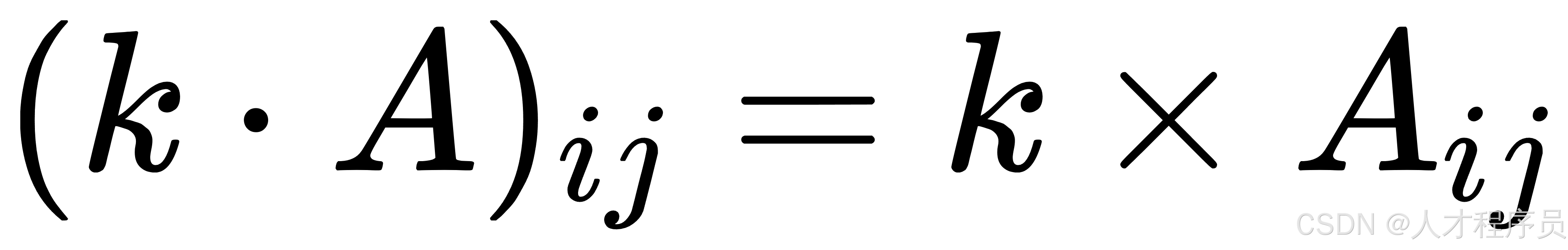
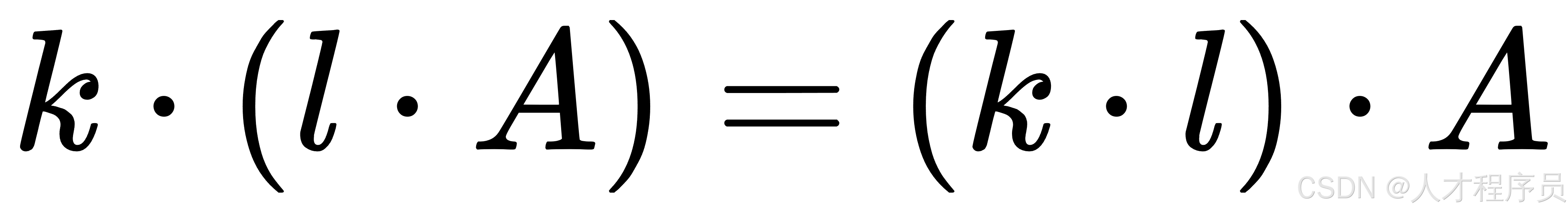
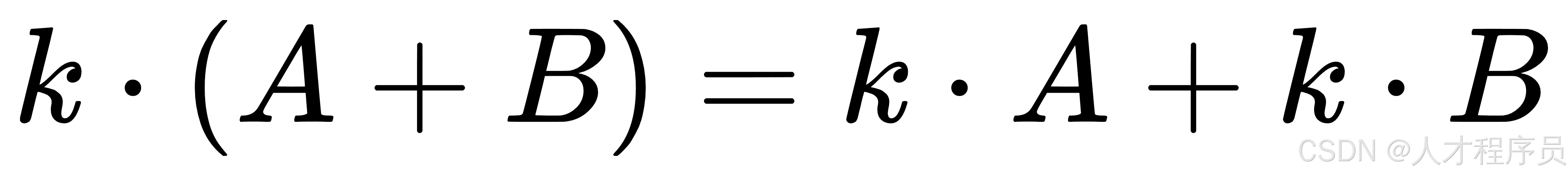
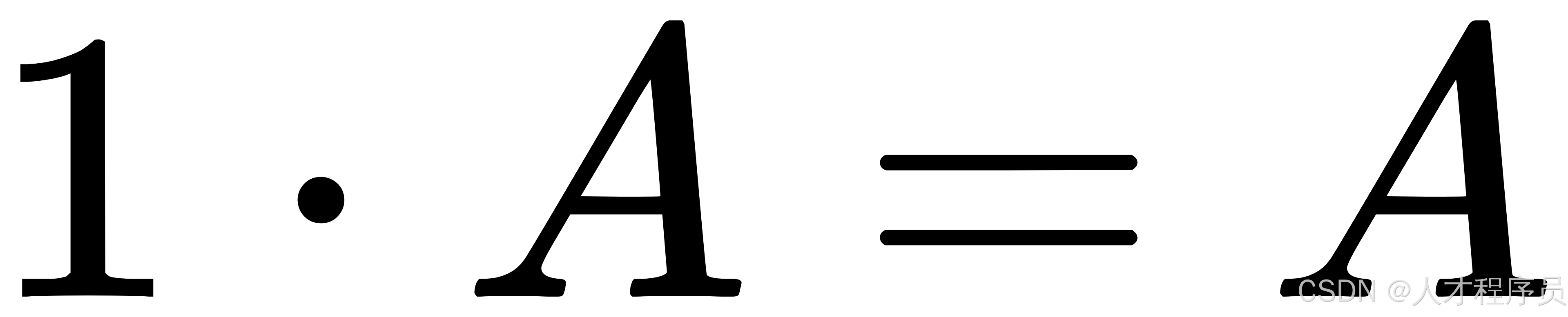
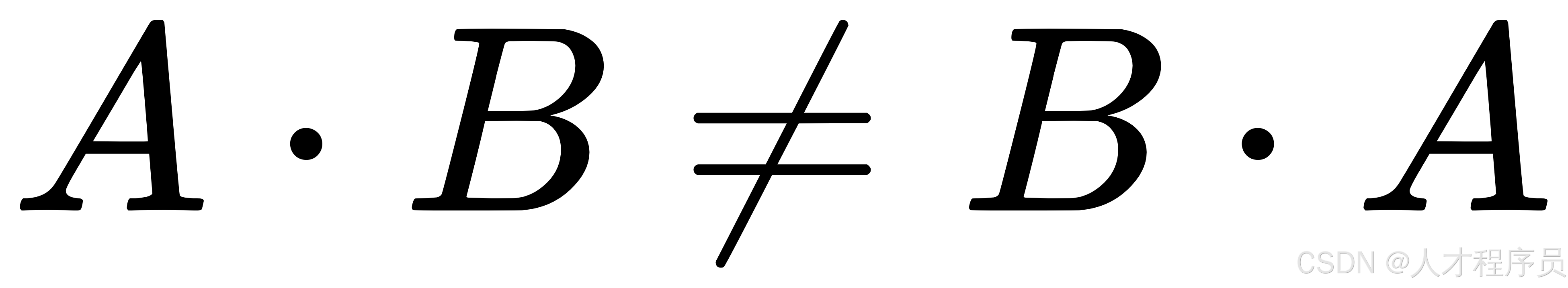
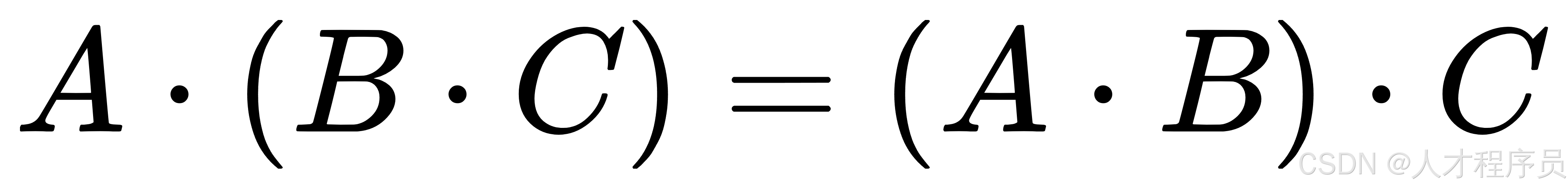
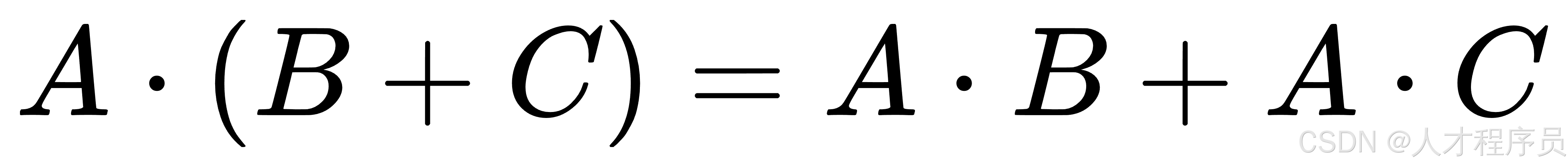

评论(0)