《深度学习笔记》二

欠拟合、正常拟合、过拟合的表现形式：

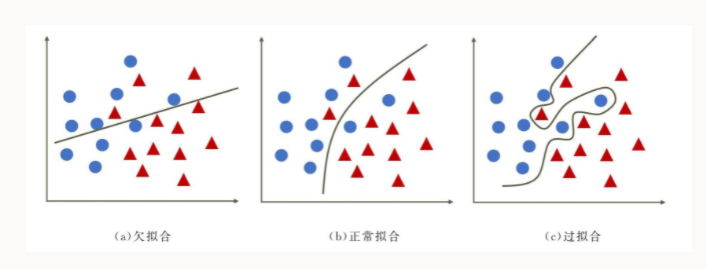
归纳出来的不是普遍规律，那就是过拟合。

所以，从这个图来看，

每次打100分，也不一定就是好事。

正则化是一种常用的技术，用于防止过拟合，并提高模型的泛化能力。正则化通常通过向损失函数添加一个正则化项来实现，这个正则化项是模型参数的某个函数，可以理解为对模型的复杂度进行惩罚。

随着正则化系数 $\lambda$逐渐增大，正则化项在模型选择中的话语权越来越高，对模型的复杂性的惩罚也越来越厉害。所以， 在实际的训练过程中， $\lambda$作为一种超参数，它在很大程度上决定了模型的生死。

而正则化项到底是什么？这就需要先了解L范数。
基于L1范数的机器学习损失函数：

L1范数和L2范数

正则化项的范数是正则化项中使用的一种距离度量方法。范数表示为 ||w||，其中 w 是模型的参数向量。不同的范数指定了不同的距离度量方法。

L1 正则化（也称为 Lasso 正则化）倾向于生成稀疏权重矩阵，而 L2 正则化（也称为 Ridge 正则化），倾向于让所有的权重都很小，在某些情况下甚至可以将一些无关的特征权重降低到零。

正则化的关键思想是在保持模型表现的同时尽量减少了参数的数量以及他们的值，这有助于减少模型泛化误差并增强其稳健性。

交叉熵损失（Cross-Entropy Loss）是机器学习中的一个常用损失函数之一，多用于二分类或者多分类问题中。

和其他损失函数一样，交叉熵损失函数可以用来衡量模型对样本的拟合程度。
如果模型产生的预测结果和真实结果比较接近，则使用交叉熵损失函数计算出的损失值会比较小；反之，如果模型的预测结果与真实结果相差较大，则损失值会比较大。通过调整模型的参数，使得损失函数的取值能够达到最小值，从而实现模型优化。

交叉熵损失函数对数值计算敏感，因此通常在神经网络中配合softmax使用。softmax将原始输出值转换为概率分布，并归一化每个类别的概率值在0到1范围内。

交叉熵损失函数的优点在于，它具备以下两个重要性质：

1. 能够有效地惩罚错误分类的样本

   当模型预测的类别概率分布与真实标签的分布越接近时，损失函数的值越小；反之，如果两者之间的差异较大，则损失函数的值就会很大。因此，交叉熵损失函数能够有效地惩罚那些错误分类的样本，推动模型向正确方向调整。

2. 能够推动模型更快地收敛

   与其他损失函数相比，比如使用MSE损失函数（均方误差（Mean Squared Error）），能够推动模型更快地收敛

需要注意的是，交叉熵损失函数对缺失数据点敏感，因此需要考虑数据集缺失情况并进行适当的处理。

本质上，Dropout也是一种正则化的方法。

它的原理和使用都比较简单，可以参考下面的图

就是在训练过程中，丢弃一些神经元，就是上图中的X。这意味着任何一个神经元，都需要不依赖于其他特定的神经元才能进行有益的分类贡献。这迫使网络学习更鲁棒和有效的特征。

避免过拟合的方法总结如下：

• 数据增强（Data augmentation）：增加原数据的数量和多样性，通过对原始数据进行旋转、翻转、平移等操作来生成新的数据，这样可以避免过拟合。
• L1和L2正则化（L1 and L2 regularization）：在损失函数中添加L1或L2正则化项，限制权重参数的变化范围，避免模型复杂度过高而引起的过拟合问题。
• 提前停止训练（Early stopping）：在训练时监控验证集上的误差，在验证误差达到最小值后停止训练，避免出现过拟合。
• Batch normalization：通过对每个batch的输入数据进行归一化，可以使得神经网络更加鲁棒，避免过拟合。
• Dropout Variational Inference: 类似dropout, 在inference的时候增加噪音，从而减少对dropout的依赖

这段概念界定，讲的非常的通俗易懂，非常不错

由于我们常常听到"所谓机器学习十大算法"这样的说法，久而久之算法就成了大家学习机器学习的直接目标。在这样的普遍观点下，线性回归、决策树、神经网络等都被划为算法的范畴。

如果一定要将线性回归等机器学习方法称为算法，也不是不行，因为算法本身就是一个广义的概念，包含了如何定义计算规则的意思，但是如果这样，那么对平方损失函数进行优化求解的最小二乘法该如何称呼呢？

对于线性回归而言，最小二乘法才是算法。那线性回归不叫算法又该叫什么呢？最好是叫模型。

在李航老师编写的《统计学习方法》一书的概念论述中，一个完整的统计学习方法包括模型、策略和算法三个要素，这是非常经典的论述。

1. 模型就是机器学习在所有的模型空间中要采用的模型类别，如线性回归和感知机模型．
2. 策略则是机器学习方法按照什么样的标准去选择最优的模型，一般也称之为模型评估方法，如线性回归的平方损失函数，我们的策略就是要让平方损失函数取到最小值；
3. 而算法则是对于策略所选的损失函数采用什么方法取到最小值，即用什么样的计算方法求解最优模型，也就是最优化问题，如求解平方损失的最小二乘法及梯度下降法。

无论是有监督学习还是无监督学习方法，都是由以上三要素构成的。

损失函数，是根据给定的参数，评估损失的一个函数。损失是目标函数计算值与标记之间的差距。
这是讨论损失函数优化的大基础。
梯度下降，考虑的是如何将损失最小化的优化方法。

而梯度下降算法的优化过程，按照顺序是下面这样的，最后发展为Adam。

1. 梯度下降 (GD)：最基本的优化算法，通过更新参数使损失函数最小化。它需要计算所有训练样本的梯度，并在每个迭代中更新参数。

2. 小批量梯度下降 (MBGD)：小批量梯度下降是梯度下降的一种变体，它一次只使用一定数量的训练样本计算梯度，并在每个迭代中更新参数，这个数量就是批量大小。相比于GD，MBGD在计算梯度时更加高效，但可能会因为不准确的梯度而导致收敛不稳定。

3. 随机梯度下降 (SGD)：MBGD的小批量如果只有一个样本，就是SGD，它在每个迭代中仅使用一个随机训练样本计算梯度，并更新参数。相比于GD和MBGD，SGD的计算复杂度更低，但收敛速度可能较慢，而且可能会因为噪声而导致收敛不稳定。

4. 动量梯度下降 (Momentum)：动量梯度下降算法引入了一个动量项，这个项可以解决SGD的收敛速度较慢和震荡的问题。该算法通过积累之前梯度的加权平均值，并将其与当前步长的梯度相结合，计算出一个更加平滑的更新步长，从而提高算法的收敛速度。

5. RMSProp：RMSProp是一种自适应学习率算法，它通过计算梯度的指数加权移动平均值，调整每个参数的学习率，从而提高算法的收敛速度。该算法主要应用于非凸优化问题。

6. Adam：Adam是一种基于动量梯度下降和RMSProp的自适应优化算法。它结合了两种算法的优点，并引入了一些额外的修正项，进一步提高算法的性能。

最后，Adam通常被认为是深度学习中最优秀的优化算法之一。

DNN（Deep Neural Network，深度神经网络）是一类多层神经网络，通常包含多个隐藏层，能够对复杂的非线性问题进行建模和解决。

CNN（Convolutional Neural Network，卷积神经网络）是一种特殊的DNN，它的隐藏层通常是由卷积层、池化层和全连接层组成。CNN通过卷积操作提取输入数据的特征，并采用池化操作降低特征图的维度，最后通过全连接层进行分类或回归。

讲CNN时，一般都是以图像输入为例。因为一张图像大量的二维数据表示就是一副欠卷的样子。

卷积操作：

主要用于提取输入数据的特征。它通过将输入数据与一组可学习的卷积核进行卷积操作，得到一组输出特征图。卷积核通常具有一定的边缘检测、纹理识别等特定的特征提取能力，通过不同的卷积核可以提取出不同的特征。

卷积核，也叫做滤波器。滤波器摊平到输入数据（比如像素矩阵）上的面积，就是感受野。
滤波器还有一个属性，叫做移动的步长（Stride），也就是感受野以如何大的步伐移动。

池化操作：

池化操作在CNN中主要用于减少特征图的维度。池化就是这么简单，就是简单粗暴的减少。比如4个我就挑1个。

可解释性(How and Why)，一直是伴随着神经网络发展的一个挥之不去的问题。
而CNN可视化，可以有助于这个问题的最终解决。
2014年Zeiler等人发表的一篇基于可视化角度理解CNN的论文，可谓CNN可视化的开山之作。

这篇论文全篇没有一个公式…这个是我最喜欢的，因为公式我一般看不懂啊…

完全用实验的方式展示了如何通过CNN训练过程中的特征、可视化展示网络训练的效果，并且可以直观的看到实验过程中对网络的调整是否有效。

1. 这篇论文其要点和思路如下：

卷积神经网络（CNN）是一种强大的深度学习模型，广泛用于图像分类、目标检测和其他计算机视觉任务。

CNN具有多个可学习滤波器层，从输入图像中提取越来越复杂的特征。

然而，理解CNN如何进行预测并不容易。

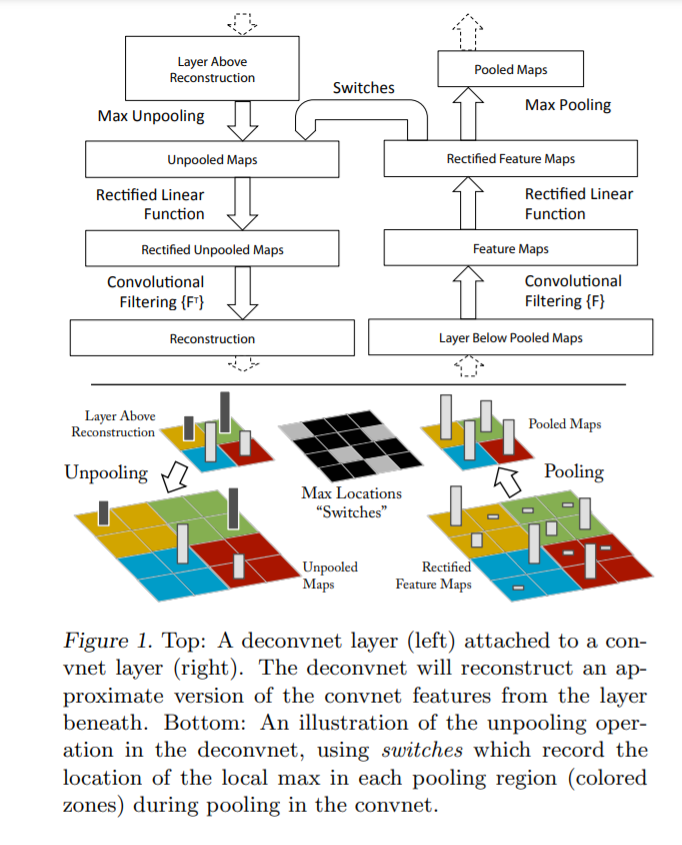
作者提出了一种名为“反卷积网络”(a multi-layered Deconvolutional Network)的方法，它将可视化已学习到的滤波器的激活映射，并从特征映射中重建输入图像。

通过分析滤波器的可视化结果，作者发现CNN会学会检测多层次的特征，从简单的边和角到复杂的物体部件和纹理。

作者还在几个基准数据集上进行了实验，证明了可视化结果有助于诊断网络错误和提高模型性能。

作者提出的方法不仅适用于CNN，还可以适应其他深度学习模型，如循环神经网络。

2. 这篇论文引入的技术：

“反卷积网络”，它是一种可视化方法，可以帮助理解卷积神经网络（CNN）中的学习到的特征。该方法可以可视化网络中的激活图和卷积层的滤波器，并从这些特征映射中重建输入图像。具体而言，反卷积网络主要由两个步骤组成：

反卷积层：将特征映射转换回像素空间。

反池化层：还原特征映射的空间分辨率，以使它们可以与反卷积层中的像素精确对齐。

这些步骤的组合可以可视化CNN中的所有层，并使用户能够查看任何学习过程的内部工作原理。

反卷积网络可视化方法的优点是可以帮助识别CNN学习的特定特征，从而使用户能够更好地理解CNN如何进行预测。因此，反卷积网络已被广泛应用于图像分类、目标检测和其他计算机视觉任务中，并为研究人员和工程师提供了强有力的工具。

3. 总结：

总的来说，这篇论文提供了对CNN内部工作机制的深入洞察，并引入了一种有用的技术，可视化和理解其学习到的特征。

最后，这篇论文可以在网上搜索阅读，一共11页。附地址是 https://arxiv.org/pdf/1311.2901.pdf

MNIST数据集是由Yann LeCun等人创建的。
Yann LeCun是一位法国计算机科学家，他是深度学习的先驱者之一。该数据集是由他创建的，旨在为机器学习算法提供一个常见的基准测试。

MNIST数据集包含手写数字的图像，它是一个非常流行的数据集，被广泛用于图像识别和深度学习的模型评估。该数据集共有60,000个训练图像和10,000个测试图像，每个图像都是28x28像素的灰度图像。这个数据集已经成为深度学习领域中的一个标准数据集，被广泛用于训练和测试各种图像识别算法。

关于作者的名字

Yann LeCun的名字看起来像中国人的名字，可能是因为他的姓氏“LeCun”有一些类似于汉语拼音的音韵，例如“乐春”。
不过，他的名字“Yann”是一个法国名字，源自于希伯来语，意思是“上帝仁慈”。因此，他的名字与中国人的名字没有什么关系，而是他的父母在取名时选择的一个法国名字。

看了这一部分后，我对可视化来解释CNN反而失去了兴趣。

感觉并没有多大的说服力。

基本做法是，对输入图像进行shape重塑、加第一层卷积，接着一层池化，然后第二层卷积，最后二层全连接层。如下图

对第一层卷积后的可视化绘图的结果：

对第二层卷积后的可视化绘图的结果：

然后解释为什么第二层卷积后可视化反而不如第一层卷积后清晰。

感觉为可视化找理由。反正说出来的都是道理。

总之，对CNN的可解释性不感兴趣了。反正有用就行。懵懂也好。