LeetCode-108. 将有序数组转换为二叉搜索树(java)
👨🎓作者：bug菌
✏️博客：、、、等
🎉简介：CSDN/阿里云/华为云/51CTO 博客专家，博客之星Top30，掘金年度人气作者Top40，51CTO年度博主Top12，掘金/InfoQ/51CTO等社区优质创作者，全网粉丝合计10w+，硬核微信公众号「猿圈奇妙屋」，欢迎你的加入！免费领取简历模板/学习资料/大厂面试真题/职业规划等海量资料。
..
✍️温馨提醒：本文字数：1999字, 阅读完需：约 6 分钟
嗨，家人们，我是bug菌呀，我又来啦。今天我们来聊点什么咧，OK，接着为大家更系列文章吧。希望能帮助更多的初学者们快速入门！
如果小伙伴们在批阅文章的过程中觉得文章对自己有帮助，请别吝啬手中的赞呀，大胆的把文章点亮👍，相信你点赞了好的文章，平台也会经常给你推荐高质量好文，您的点赞三连(收藏+关注+留言)就是对bug菌写文道路上最好的鼓励与支持😘。时光不弃🏃🏻♀️，创作不停💕，加油☘️
一、前言🔥
哈喽，小伙伴们，我是bug菌呀👀。金三银四，又到了刷题月啦。所以不管你是准备跳槽还是在职，都一起行动起来，顺应这个时代月干点该干的事儿👣。所以，赶紧跟着bug菌的步伐卷起来吧⏰，变强从这一刻开始！➕🧈
小伙伴们在批阅文章的过程中如果觉得文章对您有一丝丝帮助，还请别吝啬您手里的赞呀，大胆的把文章点亮👍吧，您的点赞三连(收藏⭐️+关注👨🎓+留言📃)就是对bug菌我创作道路上最好的鼓励与支持😘。时光不弃🏃🏻♀️，创作不停💕，加油☘️
二、题目描述：
题目：
给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
具体请看如下示例：
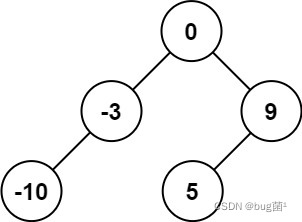
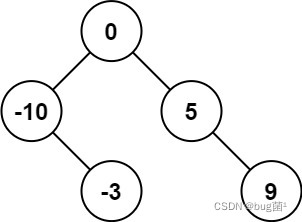
示例 1:
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：
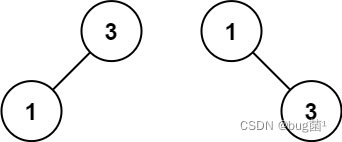
示例 2:
提示：
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
题目来源：
题目难度：⭐⭐
三、思路分析：
可能刚拿到这题的时候，小伙伴会比较懵逼，第一时间对高度平衡二叉搜索树概念不是很理解，如果解题不是很清楚题目需求，那做题简直就是噩梦，所以我先简单给大家科普下，什么是高度平衡二叉搜索树吧。
AVL树是一种高度平衡的二叉搜索树：对每一个结点x，x的左子树与右子树的高度差(平衡因子)至多为1。说白了就是高度差最大只能为1。
所以对于这题而言，我们可以分成两段递归。
因为二叉搜索树(BST)的中序遍历是升序的，因此本题等价于根据中序遍历的序列恢复BST。
所以本题需求转换一下，这样你们就好理解了。具体做法如下：
- 以升序序列中的任一个元素作为根节点。
- 以该元素左边的升序序列构建左子树，以该元素右边的升序序列构建右子树。这样得到的树就是一棵二叉搜索树啦～
- 又因为本题要求高度平衡，因此我们需要选择升序序列的中间元素作为根节点即可。
四、算法实现：
AC代码
具体算法代码实现如下：
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return dfs(nums, 0, nums.length - 1);
}
private TreeNode dfs(int[] nums, int left, int right) {
if (left > right) {
return null;
}
// 选择中间位置右边的数字作为根节点。 int mid = (left + right + 1) / 2;
TreeNode root = new TreeNode(nums[mid]);
// 递归的构建 root 的左子树与右子树。
root.left = dfs(nums, left, mid - 1);
root.right = dfs(nums, mid + 1, right);
return root;
}
}五、总结：
leetcode提交运行结果截图如下：
复杂度分析：
- 时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
- 空间复杂度：O(logn)，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度。
综上，此题虽然是道简单题，但是我觉得比一般简单题难度要高一丢丢，第一考察你们概念点，第二就是考察对概念的灵活运用。只要大家能把握这两点，其实也就不难了。
再者，解题道路千万条，欢迎小伙伴们脑洞大开，如果你们有啥更好的想法或者思路，欢迎评论区告诉我哦，大家一起互相借鉴互相学习，方能成长的更快。
好啦，以上就是本期的所有内容啦，咱们下期见咯。
... ...
好啦，以上就是这期的所有内容啦，你们学废了么？如果对你有所帮助，还请不要忘记给bug菌[三连支持]哟。如果想获得更多的学习资源或者想和更多的技术爱好者一起交流，可以关注我的公众号『』，后台回复关键词领取学习资料、大厂面经、面试模板等海量资源，就等你来拿。
六. 热文推荐🔥
滴~如下推荐【Spring Boot 进阶篇】的学习大纲，请小伙伴们注意查收。
...
七. 文末🔥
如果想系统性的学习Spring Boot，小伙伴们直接订阅bug菌专门为大家创建的Spring Boot专栏从入门到精通，从无到有，从零到一！以知识点+实例+项目的学习模式由浅入深对Spring Boot框架进行学习&使用。
如果你有一定的基础却又想精进Spring Boot，那么将会是你的最好的选择；此栏进行知识点+实例+项目的学习方式全面深入框架剖析及各种高阶玩法，励志打造全网最全最新springboot学习专栏，投资学习自己性价比最高。
我是bug菌，一名想走👣出大山改变命运的程序猿。接下来的路还很长，都等待着我们去突破、去挑战。来吧，小伙伴们，我们一起加油！未来皆可期，fighting！
- 点赞
- 收藏
- 关注作者
评论（0）