C 线性结构的两种应用——栈和队列 详解

举报
Cyan_RA9 发表于 2023/04/11 19:23:07 2023/04/11
【摘要】 C 数据结构与算法入门——栈和队列 内容分享。

目录

前言

一、栈

        1.概述 :

        2.分类 :

        3.算法:

                〇准备工作

                ①初始化

                ②压栈（进栈）:

                ③遍历 :

                ④判断栈是否为空 :

                ⑤出栈 :

                ⑥清空栈 :

                Δ代码演示

二、队列

        1.概述 :

        2.分类 :

        3.循环队列相关算法 :

                ①构成循环队列的条件

                ②"入队"

                ③"出队"

                ④判断队列是否为空

                ⑤判断队列是否已满

                Δ代码演示 :

三、完结撒❀

前言

        C 数据结构与算法入门——栈 和 队列 内容分享。

        注意 : ①代码中的注释也很重要；②不要眼高手低，自己动手跟着过一遍才能真正有收获；③可以点击文章侧边栏或者文章前面的目录进行跳转。良工不示人以朴，所有文章都会适时补充完善。感谢阅读！

一、栈

        1.概述 :

                "栈"是一种可以实现"先进后出"的存储结构。类似于向一个杯子里面装东西，先放进去的东西只能后倒出来。函数的调用，表达式的求值，内存分配，缓冲处理，迷宫问题等等都与栈有关。

        2.分类 :

                栈可分为静态栈和动态栈。

                静态栈：内核为数组，空间是连续的。

                动态栈：内核为链表，空间不连续。

                无论是静态栈还是动态栈，都满足栈"先进后出"的特点。

                本篇博客以动态栈为例，动态栈图示如下 ：

image.png

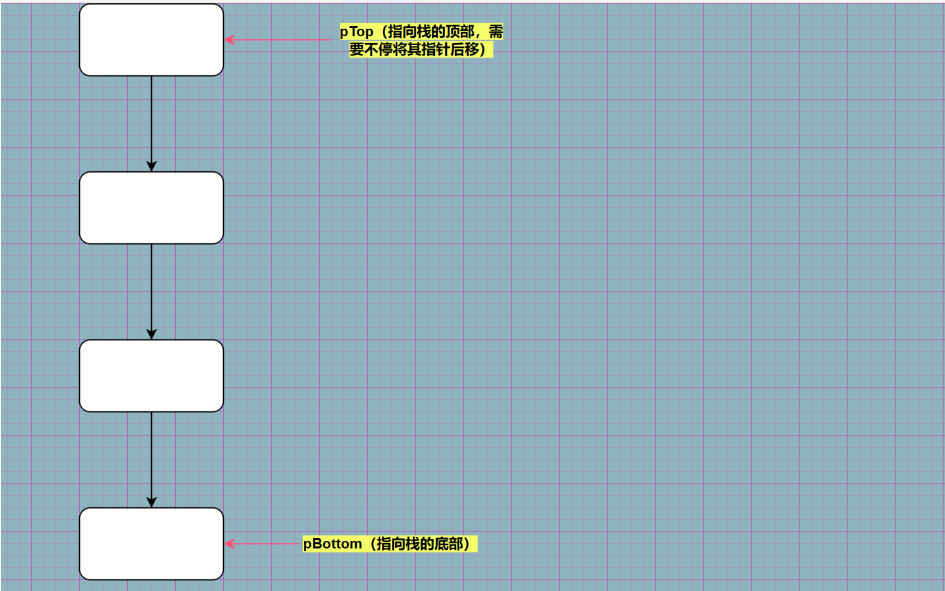
        3.算法:

                〇准备工作

                使用typedef关键字，先定义Node类型的结构体（形成链表的条件），然后再定义一个Stack类型的结构体表示栈。在Stack类型的结构体定义两个成员pTop和pBottom，将来分别指向栈中的第一个元素和最后一个元素。如下所示 ：

typedef struct Node
{
    int data;
    struct Node * pNext;
} NODE, * PNODE;
typedef struct Stack
{
    PNODE pTop;
    PNODE pBottom;
} STACK, * PSTACK;

image.gif

                注意，此处的"栈中第一个元素"指的是栈中真正意义上的第一个元素（相当于单链表中的头节点），该结点不存放有效数据。

                ①初始化

                1° 仅仅在main方法中创建一个STACK类型的变量，并不算创建好一个栈，因为此时栈中的成员pTop和pBottom的值还是垃圾值。只有当pTop和pBottom指向同一个结点（头结点）时，一个栈才算被真正地创建出来。

                2° 定义init_stack方法来完成栈的初始化，init_stack函数需要传入一个PSTACK类型的实参。init_stack方法的目的就是要让pTop和pBottom同时指向栈中的第一个元素。如下图所示 :

image.png

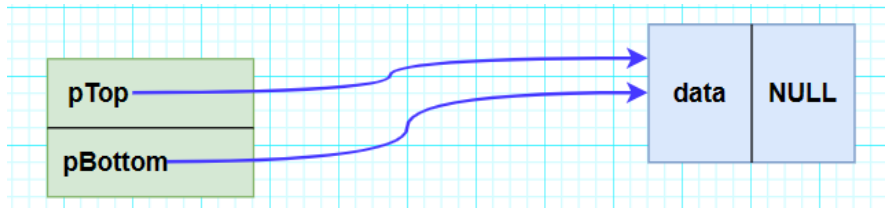
                3° 先通过malloc函数为头结点分配内存空间；然后在令pTop和pBottom指向该空间；最后令其pNext指针域为空即可。

                ②压栈（进栈）:

                1° 定义push_stack函数完成压栈的操作，push_stack函数需要传入一个PSTACK类型的实参和一个int类型的实参。（假设要存储的值为int类型）

                2° 将int类型的实参赋值给新结点的data成员。

                3° 令新结点指向pTop指向的结点（当前栈最顶部的结点），再令pTop的指针上移一位，使其指向新结点。效果如下图所示 :

image.png

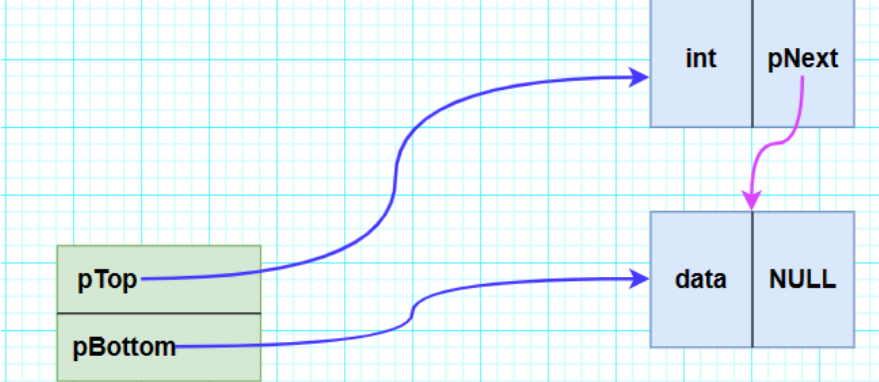
                ③遍历 :

                1° 在前面代码的基础上，定义traverse_stack函数来进行栈的遍历，只需要传入一个PSTACT类型的实参。

                2° 定义一个临时变量pDemo（PNODE类型），令其指向栈中顶部的结点。

                3° 利用while循环进行遍历，当pDemo指向的结点与pBottom指向的结点相同时停止遍历。

                4° 最终达到的效果就是自上而下遍历栈中的元素（即先进后出）。

                ④判断栈是否为空 :

                1° 在前面代码的基础上，定义is_empty函数来进行对栈是否为空的判断。

                2° 若判断栈中的pTop成员和pBottom成员指向相同，说明当前是空栈，否则不为空。

                3° 判断栈是否为空的前提，是这个栈已经初始化，如果pTop和pBottom都是垃圾值，那么认为这个栈还没有创建出来。

                ⑤出栈 :

                1° 在前面代码的基础上，定义pop_stack函数完成出栈的操作，需要传入一个PSTACK类型的实参和一个int * 类型的实参（假设出栈的是int类型元素）。其中，int * 类型的指针可以指向保存了出栈元素的值的变量。该函数的返回值类型为bool类型。

                2° 出栈，即将栈中的元素拉出来扔掉，必须按照从上往下的顺序出栈，即先进栈的后出栈，后进栈的先出栈。

                3° 先对要执行出栈操作的栈进行判断，如果该栈为空，直接false，不为空才执行出栈操作。

                4° 如果出栈成功，返回true；否则返回false。

                5° 具体出栈的流程为：先定义临时PNODE类型变量指向栈顶部的元素；将pTop成员的指针下移一位，令其指向栈当前顶部元素的下一个元素；将要出栈的结点的数据域赋值给实参中int * 类型的变量；free掉临时变量指向的结点；令临时变量为空。

                ⑥清空栈 :

                1° 在前面代码的基础上，定义clear_stack函数完成对栈清空的操作，需要传入要清空的栈的地址值，即PSTACK类型。

                2° 注意，清空不是摧毁，清空后，栈依然存在，只不过栈中没有有效元素了。

                3° 先利用is_empty函数进行判断，如果栈为空，不进行清空操作。

                4° 在clear_stack函数中定义辅助变量p和q（均为PNODE类型），p指向栈顶部的元素。

                5° 利用while 循环进行，当p指向的结点不为pBottom指向的结点时——先令q指向p下面的一个元素；再free掉p指向的空间；最后将q的指向传递给p，即令p指向了p的下一个元素；重复此过程，直到p指向栈的底部时，清空完成。

                Δ代码演示

# include <stdio.h>
# include <malloc.h>
# include <stdlib.h>
# include <stdbool.h>
typedef struct Node
{
    int data;
    struct Node * pNext;
} NODE, * PNODE;
typedef struct Stack
{
    PNODE pTop;
    PNODE pBottom;
} STACK, * PSTACK;
//函数声明
void init_stack(PSTACK);            //初始化栈，创建一个空栈
void push_stack(PSTACK, int);       //压栈（进栈）
void traverse_stack(PSTACK);        //完成栈的遍历
bool is_empty(PSTACK);              //判断栈是否为空
bool pop_stack(PSTACK, int * );     //出栈
void clear_stack(PSTACK);           //清空栈
int main(void)
{
    STACK stack;
    int val;
    init_stack(&stack);
    push_stack(&stack, 141);
    push_stack(&stack, 11);
    push_stack(&stack, 233);
    push_stack(&stack, 4);
    push_stack(&stack, 5);
    push_stack(&stack, 6);
    printf("===============遍历栈如下：===============\n");
    traverse_stack(&stack);
    printf("\n--------------------------------------------------------\n");
    printf("当前栈为空吗？");
    if (is_empty(&stack))
        printf("Yes!");
    else 
        printf("No!");
    printf("\n--------------------------------------------------------\n");
    bool b1 = pop_stack(&stack, &val);
    if (b1)
        printf("出栈成功，且出栈元素的值 = %d\n", val);
    else
        printf("出栈失败！");
    printf("\n--------------------------------------------------------\n");
    clear_stack(&stack);
    printf("清空栈后，当前栈为空吗？");
    if (is_empty(&stack))
        printf("Yes!");
    else 
        printf("No!");
    return 0;
}
void init_stack(PSTACK pStack)
{
    pStack->pTop = (PNODE) malloc(sizeof(NODE));
    if (NULL == pStack->pTop)
    {
        printf("初始化栈时，动态分配内存失败!\n");
        exit(-1);
    }
    else
    {
        pStack->pBottom = pStack->pTop;
        pStack->pTop->pNext = NULL;
    }
    return;
}
void push_stack(PSTACK pStack, int val)
{
    PNODE pNew = (PNODE) malloc(sizeof(NODE));
    if (NULL == pNew)
    {
        printf("压栈时，动态分配内存失败！\n");
        exit(-1);
    }
    pNew->data = val;               //注意 : 栈的指向是从上往下指的。
    pNew->pNext = pStack->pTop;     //必须让新结点指向栈最上面的一个结点。
    pStack->pTop = pNew;            //同时让pTop指针后移。
    return;
}
void traverse_stack(PSTACK pStack)
{
    PNODE pDemo = pStack->pTop;
    while (pDemo != pStack->pBottom)
    {
        printf("%d\t", pDemo->data);
        pDemo = pDemo->pNext;
    }
    printf("\n");
    return;
}
bool is_empty(PSTACK pStack)
{
    if (pStack->pTop == pStack->pBottom)
        return true;
    else 
        return false;
}
bool pop_stack(PSTACK pStack, int * val)
{
    if (is_empty(pStack)) 
    {
        return false;
    }
    else 
    {
        PNODE pDemo = pStack->pTop;
        pStack->pTop = pDemo->pNext;
        * val = pDemo->data;
        free(pDemo);
        pDemo = NULL;
        return true;
    }
}
void clear_stack(PSTACK pStack)
{
    if (is_empty(pStack))
        return;
    PNODE q,p = pStack->pTop;
    while (p != pStack->pBottom)
    {
        q = p->pNext;
        free(p);
        p = q;
    }
    pStack->pTop = pStack->pBottom;
    return;
}

image.gif

                运行结果 :

image.png

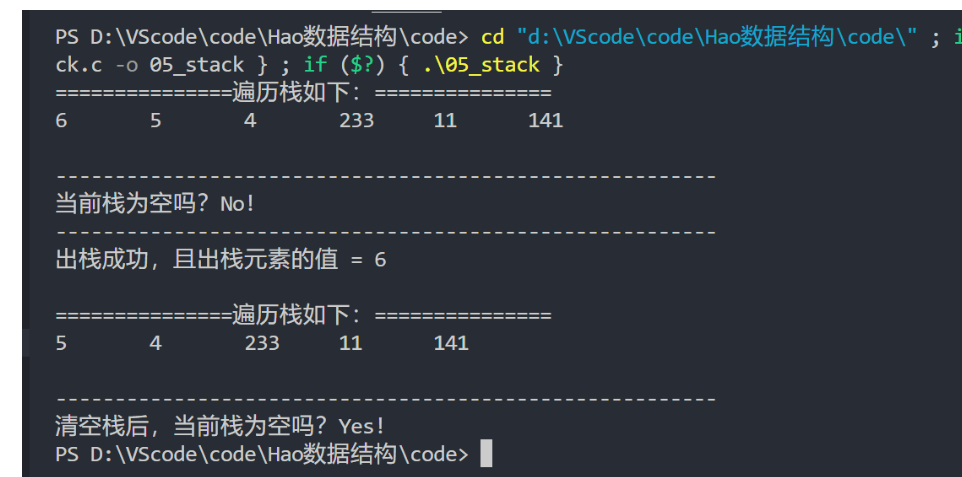
二、队列

        1.概述 :

                一种可以实现"先进先出"的存储结构。比如一个杯子底下漏了，你从上面往进倒水，它只能从下面出去，而且先进入杯子内的水一定会先从杯子底下漏出去。只要满足这种条件的存储结构，就可以称为队列。所有和时间有关的操作都与队列有关。

                向队列中添加元素称为"入队"，将队列中的元素拿出称为"出队"。（满足"先进先出，后进后出"，类似于排队。）

        2.分类 :

                链式队列 : 底层用链表实现的队列。

                链式队列效果图如下 :

image.png

                静态队列 ：底层用数组实现的队列。数组的长度决定了队列可使用空间的大小。

                静态队列效果图如下 :


                静态队列通常都必须是循环队列，即保存数组下标的front和rear是可以循环的。

                循环队列的特点，如下效果图所示 :

image.png

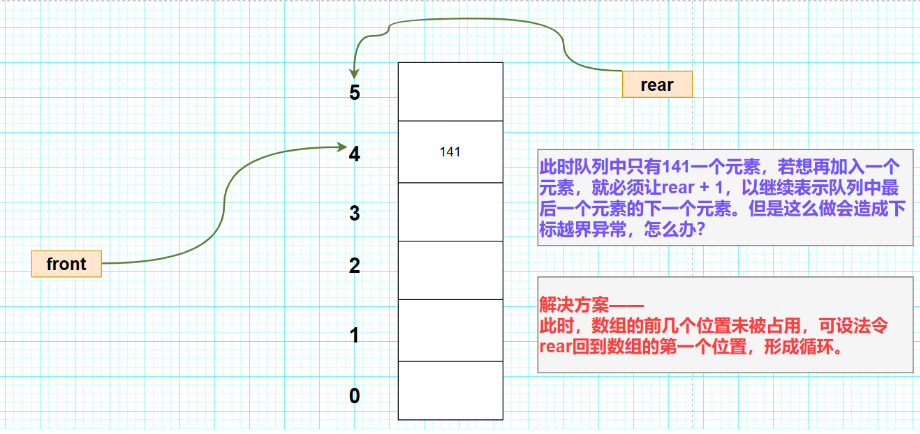
        3.循环队列相关算法 :

                ①构成循环队列的条件

                1° 需要两个参数，分别是front和rear。其中——

                当队列初始化时，front和rear的值均为0。

                当队列不为空时，front代表的是队列中的第一个元素，rear代表的是队列中最后一个有效元素的下一个元素。

                当队列为空时，front和rear的值相等，但不一定为0。

                ②"入队"

                1° 将要入队的值存入rear当前代表的位置（即当前队列的最后一个元素的下一个位置）。

                2° 改变rear 的值，具体操作为——rear = （rear+ 1) % 数组的长度。（取余）

                ③"出队"

                1° 改变front 的值，具体操作为——front = （front + 1) % 数组的长度。（取余）

                ④判断队列是否为空

                1° 根据front参数和rear参数的值来判断当前队列是否为空。

                2° 当front的值和rear的值相等时，当前队列一定为空。

                ⑤判断队列是否已满

                1° 假设数组的长度为10，如果向队列中添加10个元素，即若把某个队列填满，最终会导致front和rear表示的是同一个元素，这与前面判断队列是否为空的条件相矛盾。

                解决办法——可以另定义一个变量来保存当前队列中元素的个数，当front和rear的值相等时，增加一个判断，若当前队列中元素的个数不为0，则已满，否则为空。

                2° 更好的方法——"凡事当留馀地，得意不宜再往"。将数组中的一个位置空下，即少存一个元素。当队列中元素的个数 = 数组长度 - 1时，就认为当前队列已满。并且，随着数组长度越来越长，这一个内存空间的浪费可以忽略不计。

                if 语句的判断条件 : (((rear + 1) % 数组的长度) == front).

                Δ代码演示 : 

# include <stdio.h>
# include <stdbool.h>
# include <stdlib.h>
# include <malloc.h>
typedef struct Queue
{
    int * pBase;            //用于存储元素的数组
    int front;              //保存队列中第一个元素的下标
    int rear;               //用于保存队列中最后一个元素的下一个元素的下标
} QUEUE, * PQUEUE;
//函数声明
void init_queue(PQUEUE);        //初始化队列
bool en_queue(PQUEUE, int);     //入队
void traverse_queue(PQUEUE);    //遍历队列
bool is_full(PQUEUE);           //判断当前队列是否已满
bool is_empty(PQUEUE);          //判断当前队列是否为空
bool out_queue(PQUEUE, int * ); //出队
int main(void)
{
    QUEUE queue;
    int val;
    
    printf("当前队列为空吗？");
    init_queue(&queue);
    if (is_empty(&queue))
        printf("Yes!\n");
    else 
        printf("No!\n");
    printf("-------------------------------------\n");
    en_queue(&queue, 141);
    en_queue(&queue, 11);
    en_queue(&queue, 211);
    en_queue(&queue, 985);
    en_queue(&queue, 5);
    printf("===========遍历队列如下:===========\n");
    traverse_queue(&queue);
    printf("-------------------------------------\n");
    printf("当前队列是否已满？");
    if (is_full(&queue)) 
        printf("Yes!");
    else
        printf("No!");
    printf("\n-------------------------------------\n");
    if (out_queue(&queue, &val))
        printf("出队成功！出队的元素 = %d\n", val);
    else
        printf("出队失败！\n");
    printf("-------------------------------------\n");
        
    printf("===========遍历队列如下:===========\n");
    traverse_queue(&queue);
    return 0;
}
void init_queue(PQUEUE pQueue)
{
    pQueue->pBase = (int * ) malloc(sizeof(int) * 6);
    pQueue->front = 0;
    pQueue->rear = 0;
    return;
}
bool en_queue(PQUEUE pQueue, int val)
{
    if (is_full(pQueue))
        return false;
    pQueue->pBase[pQueue->rear] = val;
    pQueue->rear = (pQueue->rear + 1) % 6;
    return true;
}
void traverse_queue(PQUEUE pQueue)
{
    int i = pQueue->front;
    while (i != pQueue->rear)
    {
        printf("%d\t", pQueue->pBase[i]);
        i = (i + 1) % 6;
    }
    printf("\n");
    return;
}
bool is_full(PQUEUE pQueue)
{
    if (((pQueue->rear + 1) % 6) == pQueue->front)
        return true;
    else
        return false;
}
bool is_empty(PQUEUE pQueue)
{
    if (pQueue->front == pQueue->rear)
        return true;
    else
        return false;
}
bool out_queue(PQUEUE pQueue, int * pVal)
{
    if (is_empty(pQueue))
        return false;
    
    * pVal = pQueue->pBase[pQueue->front];
    pQueue->front = (pQueue->front + 1) % 6;
    return true;
}

image.gif

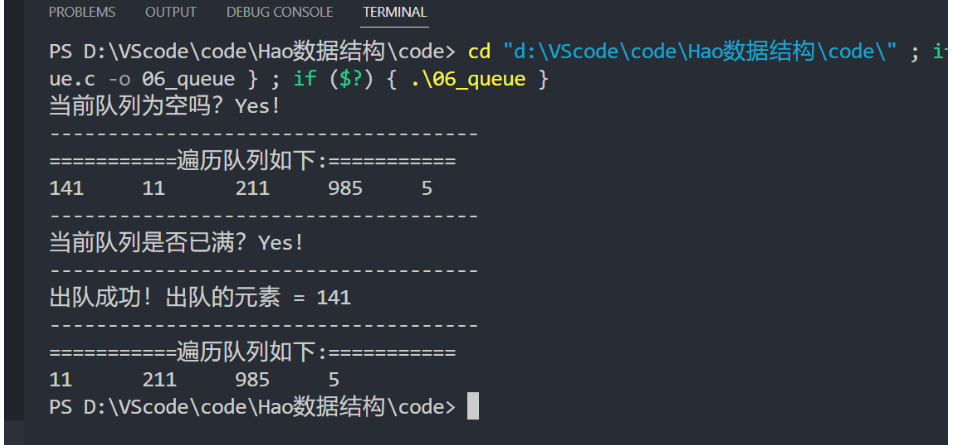
                运行结果：

image.png

三、完结撒❀

        🆗，以上就是关于栈 和 队列的全部内容了。up之后可能也会出一些算法题的讲解，不过目前在写java的博文，有时间后或许会考虑。今天就先到这里，感谢阅读！

        System.out.println("END---------------------------------------------------------------"); 

【版权声明】本文为华为云社区用户原创内容，转载时必须标注文章的来源（华为云社区）、文章链接、文章作者等基本信息， 否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
C语言 数据结构 算法
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入