无失真信源编码详解

本专栏包含信息论与编码的核心知识，按知识点组织，可作为教学或学习的参考。markdown版本已归档至【Github仓库：information-theory】，需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。

无失真信源编码

定义: 在无失真信源编码中, 编译码过程是可逆的, 即信源符号可以通过编码序列无差错的恢复 ，该编码方式适用于离散信源的编码。

实现无失真的信源编码, 要求:

a. 信源符号 $\mathrm{X}_{1} \mathrm{X}_{2} \ldots \mathrm{X}_{l} \ldots \mathrm{X}_{L}$是一一对应于码字 $\mathrm{Y}_{1} \mathbf{Y}_{2} \ldots \mathbf{Y}_{k} \ldots \mathbf{Y}_{\mathbf{K}}$ ;

b. 能够无失真或无差错地从 $\mathbf{Y}$ 恢复 $\mathbf{X}$ , 也就是能正确地 进行反变换或译码;

c. 传送 $\mathbf{Y}$ 时所需要的信息率最小。

• 信源编码器输入的消息序列: $\mathbf{X}=(\mathrm{X}_{1} \mathrm{X}_{2} \ldots \mathrm{X}_{l} \ldots \mathrm{X}_{L}) , \mathbf{X}_{l} \in\{a_{1}, \ldots a_{\mathrm{n}}\}$ ,
  输入的消息总共有 $n^{L}$ 种可能的组合
• 输出的码字为: $\mathrm{Y}=(\mathrm{Y}_{1} \mathrm{Y}_{2} \ldots \mathrm{Y}_{k} \ldots \mathrm{Y}_{K}) , \mathbf{Y}_{k} \in\{\mathbf{b}_{1}, \ldots \mathbf{b}_{\mathrm{m}}\}$
  输出的码字总共有 $m^{K}$ 种可能的组合。
• 信息率最小就是找到一种编码方式使 $\bar{K}=\frac{K}{L} \log m$ 最小

无失真定长编码定理

在定长编码中,输出码字的长度 $\mathbf{K}$ 是定值。我们的目的是寻找最小K值。

编码器输入 $\mathrm{X}=(\mathrm{X}_{1} \mathrm{X}_{2} \ldots \mathrm{X}_{l} \ldots \mathrm{X}_{L}), \mathrm{X}_{l} \in\{a_{1}, \ldots a_{\mathrm{n}}\}$ , 输入的消息总共有 $n^{\mathrm{L}}$ 种可 能的组合

输出 的码字 $\mathrm{Y}=(\mathrm{Y}_{1} \mathbf{Y}_{2} \ldots \mathrm{Y}_{k} \ldots \mathrm{Y}_{\mathrm{K}}), \mathrm{Y}_{k} \in\{\mathrm{b}_{1}, \ldots \mathrm{b}_{\mathrm{m}}\}$ , 输出的码字总共有 $m^{\mathrm{K}}$ 种可能的组合。

若对信源进行等长编码, 必须满足: $n^{\mathrm{L}} \leq m^{\mathrm{K}}$

等长编码

• 若对信源进行等长编码,必须满足: $n^{L} \leq m^{K}$ 或 $\frac{K}{L} \geq \frac{\log n}{\log m}$
• 只有当 K 长的码符号序列数 $m^{K}$ 大于或等于信源的符号数 $n^{L}$ 时,才可能存在等长非奇异码。

例 英文电报有 27 个符号, $\mathrm{n}=27, \mathrm{~L}=1, \mathrm{~m}=2$ ( 二元编码 )

$K \geq L \frac{\log _{2} n}{\log _{2} m}=\log _{2} 27 \approx 5$， 每个英文电报符号至少要用5位二元符号编码。

• 实际英文电报符号信源,在考虑了符号出现的概率以及符号之间的依赖性后,平均每个英文电报符号所提供的信息量约等于1.4比特,大大小于5比特。
• 编码后5个二元符号只携带约1.4比特信息量。

• ==等长编码的信息传输效率极低。==

等长编码定理

由 L 个符号组成的、每个符号的熵为 $\mathrm{H}(\mathbf{X})$ 的无记忆平稳信源符号序列 $\mathrm{X}_{1} \ldots \mathrm{X}_{l} \ldots \mathrm{X}_{\mathrm{L}}$ , 可用 K 个符号 $\mathbf{Y}_{1} \ldots \mathrm{Y}_{k} \ldots \mathbf{Y}_{\mathrm{K}}$ (每个符号有 $\mathrm{m}$ 种可能值)进行等长编码。

对任意 $\varepsilon>0, \delta>0$ , 只要 $\frac{K}{L} \log m \geq H(\mathrm{X})+\varepsilon$, 则当 L 足够大时, 必可使译码差错小于 $\delta$ ;

反之, 当 $\frac{K}{L} \log m \leq H(X)-2 \varepsilon$时, 译码差错一定是有限值, 而当 L 足够大时, 译码几乎必定出错.

(1) 当编码器容许的输出信息率, 也就是当每个信源符号所必须输出的码长是 $\overline{\boldsymbol{K}}=\frac{\mathrm{K}}{\mathrm{L}} \operatorname{logm}$时, 只要 $\bar{K}>H(X)$ , 这种编码器一定可以做到几乎无失真, 也就是收端的译码差错概率接近于零, 条件是所取的符号数L足够大。

(2)将定理的条件改写成

$$K \log m>L H(X)=H(\mathbf{X})$$

其中：

• 左边: K 长码字所能携带的最大信息
• 右边: L 长信源序列携带的信息量

上述定理表明：

• 只要码字所能携带的信息量大于信源序列输出的信息量, 则可以使传输几乎无失真, 当然条件是L足够大。
• 反之, 当 $\bar{K}$< $H(X)$ 时, 不可能构成无失真的编码, 也就是不可能做一种编码器, 能使收端译码时差错概率趋于零。
• $\bar{K}=H(X)$ 时, 则为临界状态, 可能无失真, 也可能有失真。

编码效率与信源长度

为了衡量编码效果, 定义编码效率:

$$\eta=\frac{H(X)}{H(X)+\varepsilon}, \varepsilon>0$$

对等长编码,若要实现几乎无失真编码,则信源长度必须满足:

$$L \geq \frac{\sigma^{2}(X)}{\varepsilon^{2} \delta}$$

其中: $\sigma^{2}(X)=E\{[I(x_{i})-H(X)]^{2}\}$ , 为信源序列的自信息方差

若信源的数学模型如下所示:

$$\left[\begin{array}{l} X \\ p \end{array}\right]=\left[\begin{array}{llll} a_{1} & a_{2} & \ldots & a_{L} \\ p_{1} & p_{2} & \ldots & p_{L} \end{array}\right], \quad H(X)=-\sum_{i=1}^{L} p_{i} \log _{2} p_{i}$$

采用码符号 {0, 1} 对该信源的每一个符号进行等长二进制编码， 则每个符号至少需要 logL 位 (bit) 才能保证得到的是唯一可译码。

$[log_2L]$向上取整。如: L=3，则至少需要2bit; L=9,则至少需要4bit。

例 设离散无记忆信源概率空间

$[\begin{array}{l} X \\ P \end{array}]=[\begin{array}{cccccccc} a_{1} & a_{2} & a_{3} & a_{4} & a_{5} & a_{6} & a_{7} & a_{8} \\ 0.4 & 0.18 & 0.1 & 0.1 & 0.07 & 0.06 & 0.05 & 0.04 \end{array}]$

• 信息熵: $H(X)=-\sum_{i} p(x_{i}) \log p(x_{i})=2.55 \mathrm{bit} / 符号$

• 方差: $\sigma^{2}(X)=\sum_{i=1}^{8} p_{i}(\log p_{i})^{2}-[H(X)]^{2}=7.82 b i t^{2} $

• 若取差错率 $\delta \leq 10^{-6}$ , 编码效率为 $90 \%$ , 则 L 应满足

  $\begin{array}{l} \varepsilon=\frac{1-\eta}{\eta} H(X) \approx 0.28 \quad L \geq \frac{\sigma^{2}(X)}{\varepsilon^{2} \delta}=\frac{7.82}{0.28^{2} \times 10^{-6}} \\ =9.8 \times 10^{7} \end{array}$

在差错率和编码效率要求并不十分苛刻的条件下, 就需要 $L=10^{8}$ 个信源符号进行联合编码, 这显然是很难实现的。

无失真变长编码定理

变长编码定理

• 在变长编码中码长K是变化的。
• 我们可根据信源各个符号的统计特性如概率大的符号用短码，概率小的用较长的码，这样在大量信源符号编成码后平均每个信源符号所需的输出符号数就可以降低，从而提高编码效率。

平均码长

对于等长码, 平均码长就是每个码字的位数, 如 例 1 的码 0 , 其平均码长为 $2 \mathrm{bit}$ ; 对于变长码, 平均码长为码字的码长的数学期, 即

$$\overline{\mathrm{K}}=\sum_{i=1}^{L} p_{i} l_{i} \text { bit }$$

其中 $l_{i}$ 为信源符号 $a_{i}$ 对应的码字的位数。

单个符号变长编码定理

若一离散无记忆信源的符号熵为 $H(X)$ , 每个信源符号用 m 进制码元进行变长编码,一定存在一种无失真编码方法, 其码字平均长度 $\bar{K}$ 或者说平均信息速率R满足下列不等式:

$$\frac{H(X)}{\log m} \leq \bar{K}(or R)<\frac{H(X)}{\log m}+1$$

离散平稳无记忆序列变长编码定理

对于平均符号熵为 $H(\mathrm{X})$ 的离散平稳无记忆信源,必存在 一种无失真编码方法,使平均信息率 $\overline{\boldsymbol{K}}$ 满足不等式

$$H(\mathbf{X}) \leq \overline{\mathbf{K}}<H(\mathbf{X})+\varepsilon$$

其中 $\varepsilon$ 为任意小正数,
平均信息速率为: $R=\frac{\bar{K}}{L} \log m$ , 表示单个符号的平均码长。 $\begin{array}{c} \overline{\boldsymbol{K}} \end{array}$是序列的平均码长。

用变长编码来达到相当高的编码效率,一般所要求的符号长度 L 可以比定长编码小得多。

编码效率的下界:

$$\eta=\frac{H(\mathbf{X})}{\overline{\mathbf{K}}}>\frac{H(\mathbf{X})}{H(\mathbf{X})+\frac{\log m}{L}}$$

若对上例用变长码实现, 要求 $\eta>\mathbf{9 0 \%}$ , 用二进制编码, $\mathrm{m}=2, \log _{2} \mathrm{~m}=\mathrm{l}$ 。
由

$\begin{aligned} \eta=\frac{H(\mathbf{X})}{\boldsymbol{R}} & >\frac{H(\mathbf{X})}{H(\mathbf{X})+\frac{\log m}{L}} \\ 0.9 & =\frac{2.55}{2.55+\frac{1}{L}} \end{aligned}$

得 $L=4$

信息率与编码效率

• 信息率

$$R=\frac{K}{L} \log m$$

• 编码效率

$$\eta=\frac{H(\mathbf{X})}{R}$$

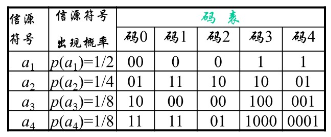
下例中，码1的平均码长为 1.5 bit, 码3的平均码长为 1.875 bit。对比信源的熵1.75bit/symbol,会有什么结?

无失真信源编码定理

Theorem . 一个熵（或熵速率) 为 $H$的信源，当信源速率为 $R$(比特/信源输出)时，只要 $R>H$，就能以任意小的错误概率进行编码。反之，如果 $R<H$, 无论采用多么复杂的编码器与译码器，错误概率不可能达到任意小，

事实上，R代表传送每个信源符号所需的平均的二进制数，称为编码速率

Illustration:若某信源的熵为H(X)=2.5bit/符号,该信源有6中输出符号，可以用3或4或任何大于2.5的比特数来代表每个符号.但是若用 2bits 去代表每个符号,错误概率将非常大或者找不到使译码错误任意小的编码方案。

参考文献：

1. Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
2. Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
3. 周炯槃. 通信原理（第3版）[M]. 北京：北京邮电大学出版社, 2008.
4. 樊昌信, 曹丽娜. 通信原理（第7版） [M]. 北京：国防工业出版社, 2012.