自信息的定义与分类

本专栏包含信息论与编码的核心知识，按知识点组织，可作为教学或学习的参考。markdown版本已归档至【Github仓库：information-theory】，需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。

自信息

信息量

如何考察或计算信源输出的消息(或者符号)的信息量?

• 信源的信息实质:不确定性（信源输出的是消息，消息的内涵是信息。信源输出一个符号，我们认为发生一个事件）。
• 数学上我们用概率（或概率密度）来表征事件不确定性的大小。

1.信息量的大小与不确定性的消除多少有关

收到某消息获得的信息量=不确定性的减少量=(收到该消息前关于某事件发生的不确定性)-(收到此消息后关于某事件发生的不确定性)

2.信道无噪声，收到某消息获得的信息量=收到该消息前关于某事件发生的不确定性=信源输出的某消息中所含的信息量。

3.概率小→不确定性大;概率大→不确定性小。

因此，某事件发生所含的信息量应该是该事件发生的先验概率的函数。

自信息定义

事件集合 $\mathbf{X}$ 中的事件 $\mathrm{x}=\mathrm{x}_{\mathbf{i}}$ 的自信息定义为 $I_{X}\left(x_{i}\right)=-\log p_{X}\left(x_{i}\right)$ 或记为: $I(x)=-\log p(x)$

注意 1 : 要求 $I(x)$ 非负. 所以对数的底数必须大于 1 .

• 底数为 2 , 单位为比特 (bit) ;
• 底数为 $\mathrm{e}$ , 单位为奈特 (Nat)；
• 底数为 10 , 单位为笛特(Det)。

1 bit =0.693 Nat =0.301 Det

注意2: I(x) 是随机变量.

自信息的含义:

• 在事件发生前, 自信息表示事件发生的不确定性。
• 在事件发生后, 自信息表示事件所包含的信息量, 是提供给信宿的信息量, 也是解除这种不确定性所需要的信息量

假设某个信源以概率p=0.25发出符号A,则A的自信息=2bit;

若某信源以概率p=0.01发出符号B，则B的自信息= $\frac{2}{lg2}$bit;

若某信源以概率p=0.99发出符号C，则C的自信息= $log_20.99$bit。

联合自信息

联合事件集合 $\mathbf{X Y}$ 中的事件 $x=x_{i}, y=y_{j}$ 的自信息定义为

$$\begin{array}{l} I_{X Y}\left(x_{i} y_{j}\right)=-\log P X\left(x_{i} y_{j}\right) \text { or } I(x y) =-\log p(x y) \end{array}$$

其中, $p(x y)$ 要满足非负和归一化的条件。

条件自信息

事件 $\mathbf{x}=\mathbf{x}_{\mathbf{i}}$ 在事件 $\mathbf{y}=\mathbf{y}_{\mathbf{j}}$ 给定条件下的自信息定义为

$$I_{X \mid Y}\left(x_{i} \mid y_{j}\right)=-\log P_{X \mid Y}\left(x_{i} \mid y_{j}\right)\text { or } I(x \mid y)=-\log p(x \mid y)$$

条件自信息的含义

• 在事件 $y=y_{j}$ 给定条件下, 在 $x=x_{i}$ 发生前的不确定性;
• 在事件 $y=y_{j}$ 给定条件下, 在 $x=x_{i}$ 发生后所得到的信息量。

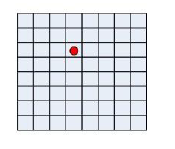
Example 有8×8=64个方格，甲将一棋子放入方格中，让乙猜。
1、将方格顺序编号，让乙猜顺序号的难度程度如何?
2、将方格按行和列编号，当甲告诉乙方格的行号后，让乙猜列顺序号的难度如何?

解：两种情况的不确定性:

1. $I(x y)=\log _{2} 64=6 b i t$
2. $I(x \mid y)=-\log _{2} p(x \mid y)=\log _{2}(1 / 8)=3 \text { bit }$

参考文献：

1. Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
2. Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
3. 周炯槃. 通信原理（第3版）[M]. 北京：北京邮电大学出版社, 2008.
4. 樊昌信, 曹丽娜. 通信原理（第7版） [M]. 北京：国防工业出版社, 2012.