已知堆叠体的三视图,求堆叠体体积:俯视图标注法的使用
【摘要】 题目 求解过程首先我们选择在俯视图上标注,因为堆叠体在垂直方向不可能出现两个立方体不接触(悬空的)状况。而左视图和主视图都可能出现两个立方体不接触的情况。我们首先在主视图里,将每一列的最大高度标注出来:将此最大高度拷贝到俯视图去:同理,将左视图的最大高度也标注出来,拷贝到俯视图去:将红色的 1 作为突破口,从1开始标。左视图的数据(红色)标在列当中,主视图的数据(蓝色)标在行当中。第一个绿...
题目

求解过程
首先我们选择在俯视图上标注,因为堆叠体在垂直方向不可能出现两个立方体不接触(悬空的)状况。而左视图和主视图都可能出现两个立方体不接触的情况。
我们首先在主视图里,将每一列的最大高度标注出来:
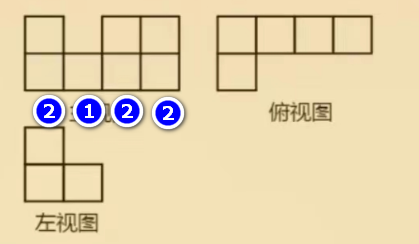
将此最大高度拷贝到俯视图去:
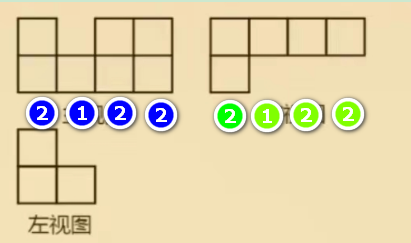
同理,将左视图的最大高度也标注出来,拷贝到俯视图去:
将红色的 1 作为突破口,从1开始标。
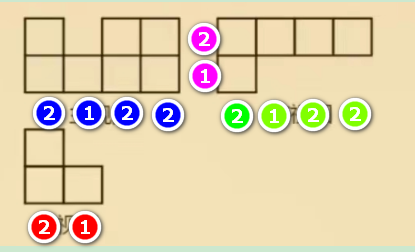
左视图的数据(红色)标在列当中,主视图的数据(蓝色)标在行当中。
第一个绿色的2,代表从前往后看过去,最多看到两个立方体。但是粉红色的1,意思是从左往右,最高只能看到1个。
因此我们得出了灰色的1. 在俯视图上标注1,意思是这个位置,有且只有1个立方体。
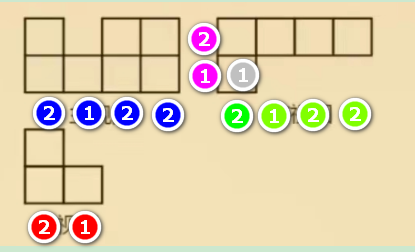
同理,上图第一个绿色的1,成为橙色1标注的依据。
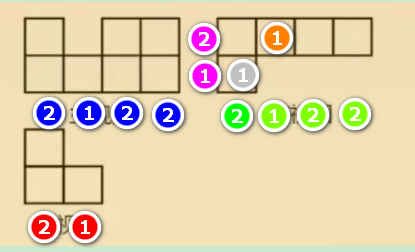
第一个绿色的2,成为俯视图里黑色2标注的依据。
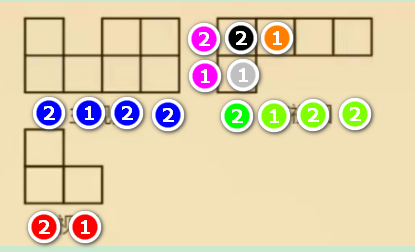
同理将俯视图最后两个位置标注出来,如下图浅蓝色所示:
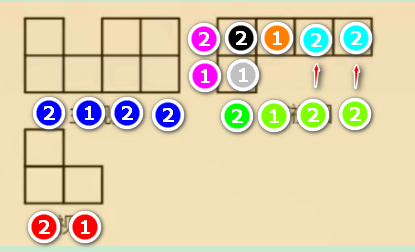
最后答案为 (2+2+2+1+1)×1×1×1 = 8
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)