量子计算(七):量子系统
量子系统
前言
对于一个非物理专业的人而言,量子力学概念晦涩难懂。鉴于此,本文仅介绍量子力学的一些基础概念加之部分数学的相关知识,甚至不涉及薛定谔方程,就足够开始量子计算机的应用。这如同不需去了解CPU的工作原理以及经典计算机的组成原理,但仍能在日常生活中使用经典计算机或者编写经典程序一样。
在接下系列文章里,彻底抛却数学公式,纯粹去介绍宽泛的概念,目的仅仅想让读者都能了解这个问题——量子究竟是什么。
如果不想被量子的诡异事实所颠覆,并且对于线性代数很有把握的话,那么可以直接过渡到后面的系列文章进行学习。
一、量子化 (Quantization)与量子态 (QuantumState)
简而言之,量子态就是一个微观粒子的状态。
描述一个粒子的状态时,总要找一些能够用来区分微观粒子的属性。在宏观世界中,假设一个人在一栋楼中活动,如果他在一层,就称处于1态;在二层,就称处于2态;在地下一层,就称于-1态。微观粒子也有这样的属性,比如它的位置。
但是假设这个人正在上楼梯,进入到一个模糊的状态,这样就不太容易区分到底是在“1态”还是“2态”,此时就需要找一些客观存在的参数去描述这一方面的属性,比如所处的海拔。通常,在日常生活中,这些描述都是连续的,因为这些参数会被分割成更小的部分。
然而,无限分割下去,直到不得不靠“几个原子”这种单位去描述物体的长度时,量子效应就出场了。薛定谔方程告诉人们,一定会遇到不可分割的最小单位,这种最小单位,统称为量子;这种现象,被称为量子化。这是量子的第一个特性。
量子化的属性有很多种,但在此优先考虑一种——能量。经过长期探索得知,原子的光谱只会有几个峰值,而不是连续的谱线,这代表了原子内电子的能量只会出现几种情况,电子不可能具有几种情况之外的中间值,这就是能量的量子化。每一种能量,被称之为一个能级。
同样以一栋楼为例,在微观的世界里面,一栋楼的楼梯被拆掉了,这使得微观粒子要么在一楼,要么在二楼,仅存在于整数的楼层,但是,这不代表微观粒子就失去了上下楼的机会。这里就是量子的第二个特性称之为跃迁。
当一个原子中的电子获得了来自原子外的能量时,它就有可能克服能级之间能量的差距,跳跃到另外一个态上面,并且这个电子也可以将自己的能量释放出来,跳跃到能量较低的能级上面。当然,能级本身是稳定的,不管怎么跃迁,电子的能量都只能处在这几个能级上,这是原则。
最后,回顾下什么是量子态呢?你可以想象一下电子处在不同的能级(类似宏观世界的楼层)上面,给这些楼层命名称之|1F>,|2F>,|3F>......,电子处于不同的能级就说明它,处在不同的量子态,这样就可以区分出来不同的量子态。如果能想象到此种情形,那就已经明白了什么是量子态了。
二、量子叠加性 (Quantum Superposition)
如果仅仅是把能级建成大楼,然后把大楼的楼梯、电梯全拆掉,并且不追问原因。这件事情倒也不难理解,然而剩余部分,就无法用普通的现实去想象了。
量子叠加性是量子的第三个特性。量子理论中,薛定谔的猫的故事是量子叠加性的一个典型示例,故事的未尾告诉我们:猫处于生与死的叠加态。什么是生与死的叠加态?既生又死?实际上,这个故事是关于量子叠加性的一个有争议的思想实验。
首先,必须接受一个假设,即量子的世界里面,同时存在几个状态是可能的。就像这栋楼里面的每个人,在不去观察他们时,他们同时存在于所有楼层,这就是量子叠加性。
但或许大家会有疑问,即便在现实生活中,也无法得知一栋大楼里面任何一个人的位置,最多了解他在办公桌上坐着的概率比较大而已,那这样就是量子叠加性吗?很遗憾,并非如此。因为某一时刻,即便无法确定,但这个人肯定存在于这栋楼某一个位置,不可能出现在这栋楼不同的位置,量子叠加不是一种概率性存在,事实上,对于量子本身,它就是同时存在于很多状态的叠加上。经过无数的实验证明,当物体小到分子、原子、电子那个级别的时候,叠加是客观存在的,尽管无人知道原因。
那么为什么我们感受不到叠加性呢?如果每个粒子都有这种叠加性,那是不是作为粒子组合的人也应该具有叠加性呢?
一个宏观物体是由巨大数量的粒子构成的集合体。一个粒子虽然是叠加的,但是一群粒子就能开始体现统计的平均性,就像连续扔一百次硬币,还是有可能出现全部是正面的情况,但是扔一亿次硬币的时候,如果没有做假,那会得到一个超于稳定的结果就是正反面各一半。何况每个人身体里的粒子比一亿还要多几亿倍的几亿倍,差不多有27-28位数那么多,所以人是绝无可能有叠加性的。
三、状态的演化(Evolution of State)
状态的演化是指量子态随时间发生变化。对于一个两能级的量子系统,量子状态的演化类似于地球上的位置随时间变化一样,量子态可以想象成一个单位球面上的点,它随时间演化就同球面上点的位置随时间发生变化类似。
四、测量和坍缩(Measurement And Collapse)
薛定谔宣称,不打开盒子,猫就处于生和死的叠加态,又称:“当我们打开盒子,经过了我们的观察,猫就会坍缩到一个确定的生、死状态上”。
什么叫做观察之后坍缩到确定的状态上?难道不是这个装置而是第一个看到猫的人决定了猫的生死吗?
这里提出量子的第四个特性:测量和坍缩假设。测量和坍缩对量子态的影响仍然是一个争议话题,所以用了“假设”这个特性的描述如下:
对于一个叠加态而言,可以去测量它,测量的结果一定是这一组量子化之后的、确定的、分立的态中的一个。测量得到任意的态的概率是这个叠加态和测量态的内积的平方,测量之后,叠加态就会缩到这个确定的态之上。
简而言之,如果在一个微观粒子处在1楼和2楼叠加态的话,只能测出来它在1楼或者2楼,这个概率是由它们的叠加权重决定的,但是一旦对这个粒子进行测量,这个粒子的状态就会发生变化,不再是原来那个既在1楼又在2楼的叠加态,而是处在一个确定的状态(1楼或者2楼)。换句话说,测量影响了这个粒子本身的状态。说明了叠加本身是一种客观存在的现象,那么测量、观察这种主观的事情是如何影响到客观叠加的呢?比较主流的理论是说因为微观粒子太小,测量仪器本身会对这个粒子产生一定的影响,导致粒子本身发生了变化。但是没有足够的证据证明这种说法 。
回到薛定谔的猫,薛定谔之所以提出这个思想实验,是想让宏观事物猫和微观事物放射性原子,建立纠缠,从而把量子力学的论异现象从微观世界引到现实世界中来。如果我们承认微观粒子具有这些叠加、坍缩的性质的话,那猫也具有了,这是薛定谔的思想。关于这个问题,目前并没有确切的证据证明猫不是处于这样的状态。通过形象的描述介绍了量子力学的一些基础概念,下面将用数学的方式将这些概念重新表述一遍。
注意:阅读下面的内容需要一定的数理基础,包括高等数学,线性代数,概率论中的基本概念。
态矢 State Vector
量子态可用线性代数中的向量来描述,在物理学中,向量常称作矢量。在量子理论中,描述量子态的向量称为态矢,态矢分为左矢和右矢。
右矢(ket):
左矢(bra):
采用竖线和尖括号的组合描述一个量子态,其中每一个分量都是复数,右上角标T表示转置。这种形式表示量子态是一个矢量。右矢表示一个n×1的列矢量,左矢表示一个1×n的行矢量。另外,在讨论同一个问题时,如果左矢和右矢在括号内的描述相同的话,那么这两个矢量互为转置共轭。
内积和外积
对于任意的两个量子态的矩阵(坐标)表示如下:
其内积定义为:
其外积定义为:
表示一个nxn矩阵。
五、两能级系统(Two Level System)
事物的二元化:0和1、无和有、高和低、开和关、天和地、阴和阳、生和死、产生和消灭。二元化是一种将事物关系简化的哲学,基于二进制的计算理论正是利用了这种哲学思想。
在谈论量子计算原理前,先了解经典计算机的工作流程。经典计算机就是在不断地处理0、1的二进制数码,它们代表着逻辑电路中的高低电平,对于这些二进制数码的产生、传输、处理、读取,最终反馈到像显示器这种输出设备上的信号,就是一个计算机的工作流程。
对于微观量子而言,有一个决定粒子性质的最直接参量这就是能量。粒子的能量只会在几个分立的能级上面取值,限制取值的可能性种类为两种,这就构成了两能级系统。除了某些特殊的情况之外,这两个能级必定能找出来一个较低的,称之为基态(ground state),记为|g>;另一个能量较高的,称之为激发态(excited state),记为|e>。
量子计算机里面也由两种状态来构成基本计算单元,只不过这里的两种状态是指量子态的|e>和|g>,这就是一个两能级系统的特征。
以列矢量的方式将它们记为:
行失量的形式记为:
和经典的比特类比,常将|e>记做0,将|g>记做1),并称之为量子比特(qubit)。
任意叠加态(superposition)|>可以写作|0>和|1>的线性组合
其中复数和称为振幅(amplitudes),并且满足归一化条件
其中表示复数的模。
六、状态的演化(Evolution of State)
量子态可以由态矢(或称向量)来表示,量子也可以有不同的状态,并且可以同时处于不同的状态,那么量子态是如何随时间演化呢?如下例:
假设:封闭的(closed)量子系统的演化(evolution)由酉变换(unitary transformation)来描述。具体地,在t1时刻系统处于状态|>,经过一个和时间t1和t2有关的酉变换U,系统在t2时刻的状态
这里的酉变换U可以理解为是一个矩阵,并且满足
其中U+表示对矩阵U取转置共轭。根据可逆矩阵的定义可知,U也是一个可逆矩阵,因此西变换也是一个可逆变换。而在量子计算中,各种形式的酉矩阵被称作量子门。
例如Pauli矩阵也是一组酉矩阵
以X门作用在量子态上为例
再如X门作用在任意的量子态上
从上述中看出,量子态的演化本质上可以看作是对量子态对应的矩阵做变换,即是做矩阵的乘法。由于X门和经典逻辑门中的非门类似,有时也常称X门为量子非门(quantum NOT gate)。
七、置加态和测量(Superposition State And Measurement)
按照态矢的描述,这两个矢量可以构成一个二维空间的基。任何一个态都可以写为这两个基在复数空间上的线性组合,即
其中表示模为1幅角为的复数
可以定义测量就是将量子态投影到另一个态|>上。获得这个态的概率是它们内积的平方,即
其它概率下会将量子态投影到它的正交态上去,即
则量之后量子态就坍缩到测量到的态上。
八、相位、纯态和混合态( Phase,Pure State and Mixed State)
如果将量子态初始化到某一个未知的叠加态上面,能否通过反复的测量得到它的表达式呢?看以下这两种情况:
发现在|0>,|1>的方向上测量,它们的表现都是一半概率为0,一半概率为1,根本不能区分。从这个现象可以知道无法通过概率得到态的相位信息0,实际上,量子态的相位是量子相干性的体现。
另一种情况,假设左手抓着一个袋子,这个袋子里面有无数的量子态,它们全都是这种叠加态;另外,有一个机器可以在|0>,|1>的方向上测量。
每次拿出一个态,对它进行测量,不管它是0,还是1,都扔到右手边的另一个袋子里面,如此反复,这样右边袋子里面的态越来越多了。由于测量结果对于这两种情况是等概率的,所以袋子里面约有一半的态是|0>,另一半是|1>。
假设从右边的袋子里取出一个,在不知道手上的态是什么情况下,能说它和左边袋子里的态一样都是吗?
答案是不能。右边袋子里的态,实际上是一种经典的概率叠加,和等量的红球白球装在袋子里面一样。这样的态是不具有相位的。它只能表示为
这种类似于概率列表的形式。
所以,定义纯态就是“纯粹的量子态”,它不仅具有概率,还具有相位也就是量子相千性。混合态是纯态的概率性叠加,它往往失去了部分或全部的相位信息。
九、密度矩阵和布洛赫球(Density Matrix And Bloch Spher)
态矢是对纯态的描述,如果要描述一个混合态,就必须写成态集合和概率的列表形式,非常烦琐,因此采用密度矩阵来描述。
对于一个纯态而言,密度矩阵的形式是:
而对于一个混合态而言,密度矩阵的形式是:
其中是系统所处的态及其概率。
密度矩阵有以下的性质:
对于一个两能级体系表述的态,不论是纯的还是混合的的都可以用密度矩阵表示
当且仅当量子态时纯态时成立。
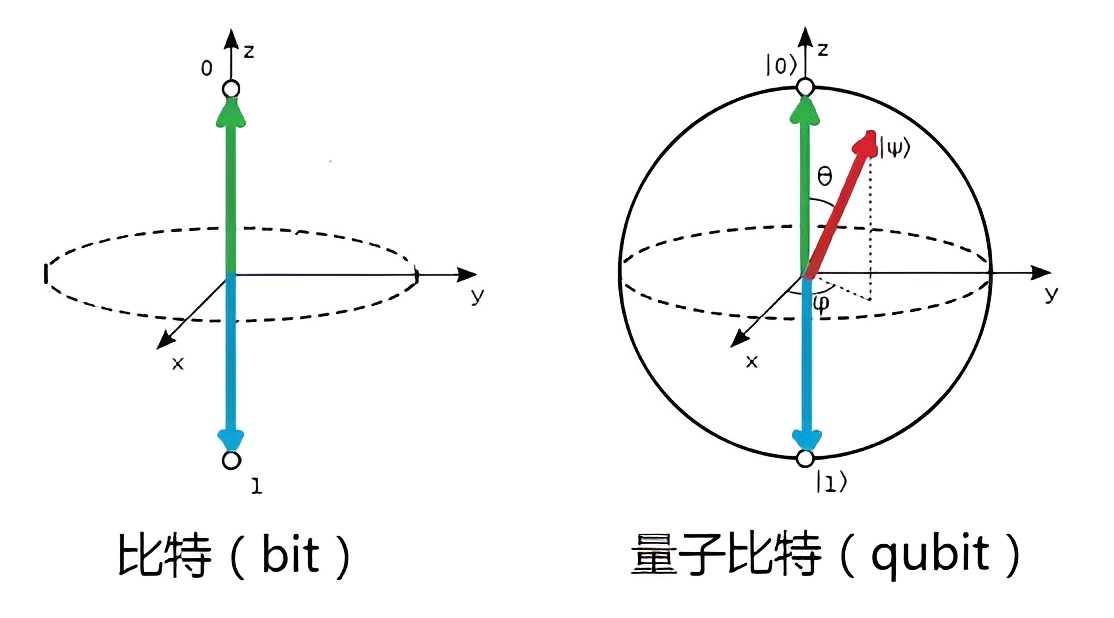
对角线上的分量表示整个系统如果经历一次测量,那么可以得到这个态的概率。如果只去操作和测量一个两能级体系,那么是分辨不出相同的密度矩阵的。密度矩阵已经完备地表示了一个两能级系统可能出现的任何状态。为了更加直观地理解量子叠加态与逻辑门的作用,引入布洛赫球的概念,它能够方便地表示一个量子比特的任意状态。
如果量子态是一个纯态,那么它是球面上的点。点的z坐标衡量了它的|0>和|1>的概率,即
最上面表示|0>态,最下面表示|1>态。
再沿着平行于XY平面的方向,并且穿过这个点的Z坐标,可以得到一个圆,这个圆就象征着相位的复平面;这个点在这个圆上交X轴的角度就是单位复数的幅角。经过这个过程可以将每个纯态都与球面上的点一一对应了起来。
对于混合态而言,因为根据之前的描述,混合态实际上是多个纯态的经典统计概率的叠加。对于每一个纯态分量,连接球心和球面上的点,可以形成一个矢量。根据概率列表,对所有的纯态矢量进行加权平均,即可得到混合态的矢量,即得到了混合态对应的点。
混合态是布洛赫球内部的点,根据混合的程度不同,矢量的长度也不同。最大混合态是球心,它意味着这里不存在任何量子叠加性。
例如(1,0,0)和(-1,0,0)点在布洛赫球上就是在X方向上的顶点和-X方向上的顶点。它们对应的量子态的概率分布就是Z坐标,即为0。
沿XY平面横切,得到一个圆,可以看到这两个点对应的幅角是,,由此推断出量子态分别为:
如果将这两个态以1/2,1/2的概率混合,在布洛赫球上面的坐标将表示为(0,0,0),也就是球心。对应到密度矩阵的表述为:
即为最大混合态。
- 点赞
- 收藏
- 关注作者





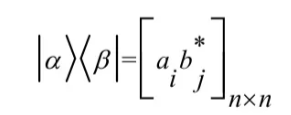

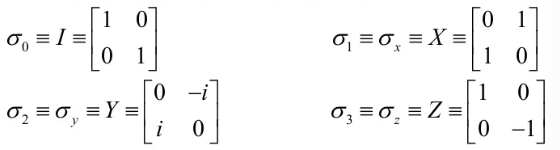
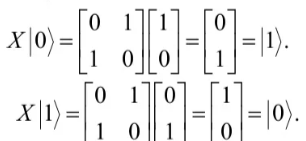
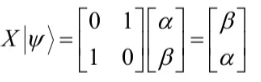
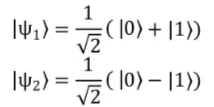
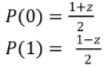

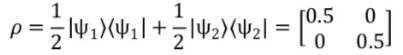

评论(0)