0. 简介

相较于激光雷达而言，视觉SLAM除了点特征以外还多出了线特征以及面特征。相比于点特征而言，线特征和面特征在单一环境中会更有鲁棒性。这篇文章中作者将会围绕着线特征和面特征的数学特性进行介绍

1. 线特征

线特征：优点在于具有天然的光照及视角不变性，同时更高级的特征也使追踪的鲁棒性和准确性有所提高。特别是在特定的人造场景（室内，走廊）等场景，能够克服无纹理或者不可靠纹理带来的干扰。

而其缺点也很明显,在于线段的检测及匹配耗时相对特征点更大。同时在后端也没有一个标准且通用的SLAM优化及回环模块。线特征匹配也是较为困难的，如线段易断裂，不具备强有力的几何约束（如极线几何约束），在纹理缺失处不具有较强的辨识度等。

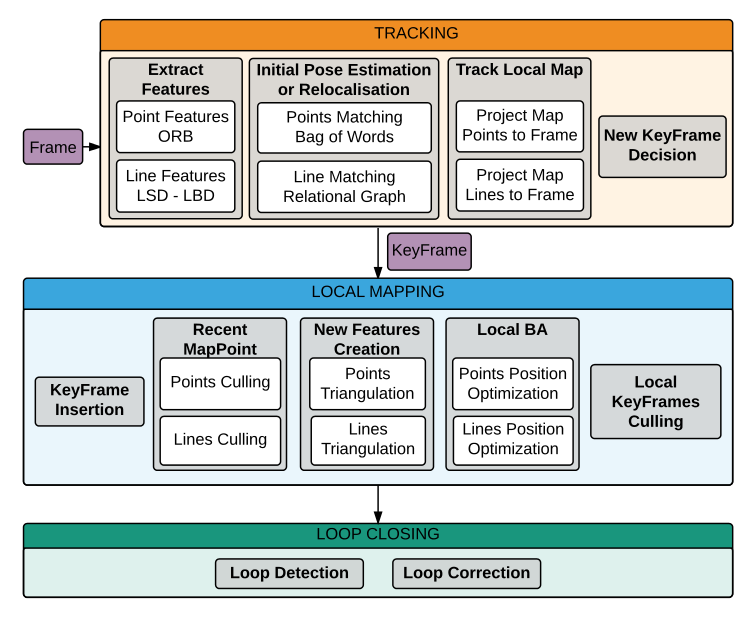
线特征的典型代表是PL-SLAM，该框架是在ORB-SLAM的框架基础之上，添加了一些与线特征有关的模块，从而构建了一套单目SLAM系统。整个系统的框架如下图所示：

对于线的描述，采用了 端点(endpoints) 的方法，毕竟现实中，几乎不不可能碰到无限延伸的直线，几乎都是线段，所以，用端点的方法来描述直线是比较合理的。我们假设 $P,Q\in R^3$是空间直线的两个端点， $p_d,q_d\in R^2$是其在图像中的投影坐标，另外，记 $p_d^h,q_d^h \in R^3$ 是对应的齐次坐标。于是，我们可以得到直线的参数： $I =p_d^h,q_d^h /|p_d^h,q_d^h |$ 。

Tip：（对于向量(x,y,1)，可以在几何意义上理解为是在【第三维为常数的】平面上的一个二维向量。这种用【三】维向量表示【二】维向量，或者一般而言，用一个n+1维的向量表示一个n维向量的方法称为齐次坐标表示法。】）。

这样我们就可以得到线特征所需要的参数。然后是定义线的重投影误差（line reprojection error） $E_{line}$——投影线段的端点与在图像中检测到的直线之间的点到直线距离 $E_{pl}$之和： $E_{line}(P,Q,I,\theta,k) = E_{pl}^2(P,I,\theta,k) + E_{pl}^2(Q,I,\theta,k)$。而 $E_{pl} = I^T\pi(P,\theta,K)$。

其中， $I$为上面提到的直线参数， $\pi(P,\theta,K)$ 为空间点 $P$投影到图像平面的坐标，而其中的 $\theta,K$分别为相机的外参 $\{R,t\}$和内参。理想情况下，空间点 $P$的投影点是在直线上的，所以点到直线距离 $E_{pl} = 0$，或者说，点在直线上。

通过这样的计算就可以获取到两条线之间的重投影误差了。

2. 面特征

…详情请参照古月居