SLAM 中的 Kalman Filter 推导

前言

本篇博客主要还是进行不同卡尔曼滤波的数学推导，不会具体涉及到某些传感器。在理解了卡尔曼滤波的数学模型后，对于不同传感器只需要将其测量模型套入运动/观测模型即可。关于基于不同传感器的滤波融合方案，准备之后在阅读论文时再分别整理。

1. SLAM 中的定位概率模型

在 SLAM 问题中，我们想要通过滤波方法求解的问题是：求解一个后验概率，即给定一系列观测（和输入）和初始时刻的先验位姿，估计每一个时刻的位姿，如下所示。

$$p(\boldsymbol{x}_k | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k})$$

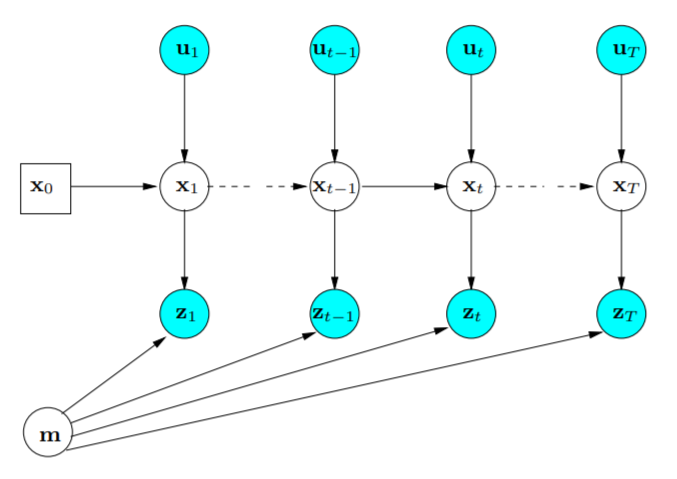
其中， $\boldsymbol{x}_0$ 为先验位姿， $\boldsymbol{u}_{1:k}$ 为 $1:k$ 时刻的输入， $\boldsymbol{z}_{0:k}$ 为 $0:k$ 时刻对环境的观测。我们可以将这些变量通过一个图来表示：

可以看出，在这种图模式下，每个状态仅仅依赖于前一时刻的位姿和输入，和历史位姿无关，这体现了一阶马尔科夫性。同理，观测也只和对应时刻的位姿（以及环境）有关。利用贝叶斯公式对后验概率进行展开有：

$$\begin{aligned} p(\boldsymbol{x}_k|\boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k}) &= \frac{p(\boldsymbol{z}_k | \boldsymbol{x}_k, \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})p(\boldsymbol{x}_k | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})}{p(\boldsymbol{z}_k|\boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})} \end{aligned}$$

上式即为最基本的贝叶斯滤波公式求解当前状态的后验概率，公式可以分为三部分：

• $p(\boldsymbol{z}_k | \boldsymbol{x}_k)$：当前时刻，当前状态下对环境的观测
• $p(\boldsymbol{x}_k| \boldsymbol{x}_{k-1}, \boldsymbol{u}_{k})$：从前一时刻到当前时刻的状态变化预测
• $p(\boldsymbol{x}_{k-1} | \boldsymbol{x}_0, \boldsymbol{u}_{1:k}, \boldsymbol{z}_{0:k-1})$，上一时刻的状态后验概率

因此，用比较通俗的话来描述一下贝叶斯滤波的过程：

• 首先获得上一时刻状态的后验概率分布
• 对上一时刻所有可能的状态根据运动模型对当前状态进行预测，获得当前状态的先验分布
• 结合当前状态的先验分布和当前观测结果的概率分布计算得到当前状态的后验分布

这个流程中涉及两个部分：怎么从上一时刻的状态量结合输入预测当前时刻状态量；怎么在当前状态下获得对环境的观测分布。这分别对应系统中的两个模型：

运动模型：

$$\boldsymbol{x}_k = f(\boldsymbol{x}_{k-1}, \boldsymbol{u}_k, \boldsymbol{w}_k)$$

观测模型：

$$\boldsymbol{z}_k = f(\boldsymbol{x}_k, m, \boldsymbol{v}_k)$$

其中， $\boldsymbol{w}_k, \boldsymbol{v}_k$ 分别是运动模型和观测模型的噪声， $m$ 为环境信息。如果问题中不需要对环境信息估计的话，可以不考虑，在大部分视觉 SLAM 中会对环境中的特征点进行优化，此时，特征点会作为环境信息纳入优化中。

2. 卡尔曼滤波 Kalman Filter

原始卡尔曼滤波推导

卡尔曼滤波假设位姿和观测符合高斯分布，且运动模型和观测模型都是线性的，因此运动模型和观测模型可以写成以下形式：

$$\begin{aligned} \boldsymbol{x}_k &= \boldsymbol{F}_k\boldsymbol{x}_{k-1} + \boldsymbol{G}_k\boldsymbol{u}_k + \boldsymbol{w}_k, \qquad &\boldsymbol{w} \sim \mathcal{N}(0, \boldsymbol{W})\\ \boldsymbol{z}_k &= \boldsymbol{H}_k\boldsymbol{x}_k + \boldsymbol{v}_k, \qquad &\boldsymbol{v} \sim \mathcal{N}(0, \boldsymbol{V}) \end{aligned}$$

为了把状态和先验和后验估计区分开，用 $\check{\boldsymbol{x}}$ 表示先验估计，用 $\hat{\boldsymbol{x}}$ 表示后验估计。其中运动模型中，上一时刻的状态后验写为：

$$p(\boldsymbol{x}_{k-1}|\boldsymbol{x}_0, \boldsymbol{u}_{1:k-1}, \boldsymbol{z}_{0:k-1}) = \mathcal{N}(\hat{\boldsymbol{x}}_{k-1}, \hat{\boldsymbol{P}}_{k-1})$$

基于运动模型得到当前时刻的状态位姿的预测值同样服从高斯分布：

$$\check{\boldsymbol{x}}_k \sim \mathcal{N}(\check{\boldsymbol{\mu}}_k, \check{\boldsymbol{P}}_k)$$

预测值（先验分布）的均值和协方差矩阵根据运动模型和高斯分布下方差传播的性质得到：

$$\begin{aligned} \check{\boldsymbol{\mu}}_k &= \check{\boldsymbol{x}}_k = \boldsymbol{f}(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_k, \boldsymbol{0}) = \boldsymbol{F}_k\boldsymbol{x}_{k-1} + \boldsymbol{G}_k\boldsymbol{u}_k\\ \check{\boldsymbol{P}}_k &= \boldsymbol{F}_{k-1}\hat{\boldsymbol{P}}_{k-1}\boldsymbol{F}_{k-1}^T + \boldsymbol{W}_k \end{aligned}$$

显然这一步我们得到的当前时刻的状态值估计的不确定度由于引入了运动误差，相比于上一时刻的不确定度变大了。观测模型的作用就是根据观测估计当前状态的后验概率，降低不确定度。

卡尔曼滤波可以分为以下几个阶段：

首先计算当前时刻状态量预测值的均值和方差：

$$\begin{aligned} \check{\boldsymbol{\mu}}_k &= \check{\boldsymbol{x}}_k = \boldsymbol{F}_k\boldsymbol{x}_{k-1} + \boldsymbol{G}_k\boldsymbol{u}_k\\ \check{\boldsymbol{P}}_k &= \boldsymbol{F}_{k-1}\hat{\boldsymbol{P}}_{k-1}\boldsymbol{F}_{k-1}^T + \boldsymbol{W}_k \end{aligned}$$

然后，计算以下式子，定义为卡尔曼增益：

$$\boldsymbol{K}_k = (\check{\boldsymbol{P}}_k\boldsymbol{H}^T)(\boldsymbol{H}\check{\boldsymbol{P}}_k\boldsymbol{H}^T + \boldsymbol{V})^{-1}$$

最后，对预测值使用卡尔曼增益和观测值进行更新：

$$\begin{aligned} \hat{\boldsymbol{\mu}}_k = \hat{\boldsymbol{x}}_k &= \check{\boldsymbol{x}}_k + \boldsymbol{K}_k(\boldsymbol{z}_k - \boldsymbol{H}\check{\boldsymbol{x}}_k)\\ \hat{\boldsymbol{P}}_k &= (\boldsymbol{I} - \boldsymbol{K}_k\boldsymbol{H})\check{\boldsymbol{P}}_k \end{aligned}$$

def kf_predict(X0, P0, A, Q, B, U1):
    X10 = np.dot(A,X0) + np.dot(B,U1)
    P10 = np.dot(np.dot(A,P0),A.T)+ Q
    return (X10, P10)


        
def kf_update(X10, P10, Z, H, R):
    V = Z - np.dot(H,X10)
    K = np.dot(np.dot(P10,H.T),np.linalg.pinv(np.dot(np.dot(H,P10),H.T) + R))
    X1 = X10 + np.dot(K,V)
    P1 = np.dot(1 - np.dot(K,H),P10)
    return (X1, P1, K)

原始卡尔曼滤波要求运动模型和观测模型都是线性的，这在实际情况下通常不满足，因此下面几个卡尔曼滤波的变种就是将卡尔曼滤波应用在非线性系统下的几种思路。

3. 扩展卡尔曼滤波 Extended Kalman Filter (EKF)

扩展卡尔曼滤波的思路比较简单。既然卡尔曼滤波只能用在线性系统下，那么只要对非线性系统进行线性化就可以了。因此，对运动模型和观测模型使用泰勒展开进行线性化：

$$\begin{aligned} \boldsymbol{x}_k &= f(\boldsymbol{x}_{k-1}, \boldsymbol{u}_k, \boldsymbol{w}_k)\\ &\approx f(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_k, \boldsymbol{0}) + \left.\frac{\partial f}{\partial \boldsymbol{x}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \boldsymbol{0}}(\boldsymbol{x}_{k-1} - \hat{\boldsymbol{x}}_{k-1}) + \left.\frac{\partial f}{\partial \boldsymbol{w}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \boldsymbol{0}}(\boldsymbol{w}_k - \boldsymbol{0})\\ \boldsymbol{z}_k &= h(\boldsymbol{x}_{k}, \boldsymbol{v}_k)\\ &\approx h(\check{\boldsymbol{x}}_{k}, \boldsymbol{0}) + \left.\frac{\partial h}{\partial\boldsymbol{x}}\right|_{\check{\boldsymbol{x}}_{k}, \boldsymbol{0}}(\boldsymbol{x}_{k} - \check{\boldsymbol{x}}_{k}) + \left.\frac{\partial h}{\partial\boldsymbol{v}}\right|_{\check{\boldsymbol{x}}_k, \boldsymbol{0}}(\boldsymbol{v}_k - \boldsymbol{0}) \end{aligned}$$

将上式中四个雅可比分别用四个矩阵表示：

$$\begin{aligned} \boldsymbol{F}_k &= \left.\frac{\partial f}{\partial \boldsymbol{x}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \boldsymbol{0}}\\ \boldsymbol{Q}_k &= \left.\frac{\partial f}{\partial \boldsymbol{w}}\right|_{\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}, \boldsymbol{0}}\\ \boldsymbol{H}_k &= \left.\frac{\partial h}{\partial\boldsymbol{x}}\right|_{\check{\boldsymbol{x}}_{k}, \boldsymbol{0}}\\ \boldsymbol{R}_k &= \left.\frac{\partial h}{\partial\boldsymbol{v}}\right|_{\check{\boldsymbol{x}}_k, \boldsymbol{0}} \end{aligned}$$

因此，线性化式子可以写成：

$$\begin{aligned} \boldsymbol{x}_k &\approx \check{\boldsymbol{x}}_{k} + \boldsymbol{F}_{k-1}(\boldsymbol{x}_{k-1} - \hat{\boldsymbol{x}}_{k-1}) + \boldsymbol{Q}_k\boldsymbol{w}_k\\ \boldsymbol{z}_k &\approx \check{\boldsymbol{z}}_k + \boldsymbol{H}_k(\boldsymbol{x}_{k} - \check{\boldsymbol{x}}_{k}) + \boldsymbol{R}_k\boldsymbol{v}_k \end{aligned}$$

接下来为了求卡尔曼增益，我们需要求线性化后的运动模型和观测模型的均值和协方差：

运动模型：

$$\begin{aligned} E[\boldsymbol{x}_k] &= \check{\boldsymbol{\mu}}_k = E[\check{\boldsymbol{x}}_{k} + \boldsymbol{F}_{k-1}(\boldsymbol{x}_{k-1} - \hat{\boldsymbol{x}}_{k-1}) + \boldsymbol{Q}_k\boldsymbol{w}_k]\\ &= \check{\boldsymbol{x}}_{k} + \boldsymbol{F}_{k-1}(\boldsymbol{x}_{k-1} - \hat{\boldsymbol{x}}_{k-1}) + \hat{\boldsymbol{x}}_{k-1})\\ E[(\boldsymbol{x}_k - E[\boldsymbol{x}_k])(\boldsymbol{x}_k - E[\boldsymbol{x}_k])^T] &= \check{\boldsymbol{P}}_k \approx E[\boldsymbol{Q}_k\boldsymbol{w}_k\boldsymbol{w}_k^T\boldsymbol{Q}_{k}^T]\\ &= \boldsymbol{Q}_k\boldsymbol{W}\boldsymbol{Q}^T \end{aligned}$$

同理可得观测模型：

$$\begin{aligned} E(\boldsymbol{z}_k) &\approx \check{\boldsymbol{z}}_k + \boldsymbol{H}_k(\boldsymbol{x}_k - \check{\boldsymbol{x}}_k)\\ E((\boldsymbol{z}_k - E(\boldsymbol{z}_k))(\boldsymbol{z}_k - E(\boldsymbol{z}_k))^T) &\approx E[\boldsymbol{R}\boldsymbol{v}_k\boldsymbol{v}_k^T\boldsymbol{R}^T] = \boldsymbol{R}\boldsymbol{V}\boldsymbol{R}^T \end{aligned}$$

class ExtendedKalmanFilter(DataFilter):
    def __init__(self, state_dimension: int, observations_dimension: int):
        self.observations_dimension = observations_dimension
        self.state_predicted = np.zeros((state_dimension,))
        self.state_dimension = state_dimension
        self.covariance_predicted = np.matrix(np.zeros((state_dimension, state_dimension)))

    def set_initial(self, initial_state: np.array, initial_covariance_estimate: np.matrix):
        if initial_state.shape != (self.state_dimension, ):
            raise ValueError("Incorrect dimension for initial state")

        if initial_covariance_estimate.shape != (self.state_dimension, self.state_dimension):
            raise ValueError("Incorrect dimension for state covariance")

        self.state_predicted = initial_state
        self.covariance_predicted = initial_covariance_estimate

    def _predict(self, transition_function: Callable[[np.array, np.array], np.array], control_input: np.array,
                 process_covariance: np.matrix) -> None:

        self.state_predicted = transition_function(self.state_predicted, control_input)
        transition_matrix = nd.Jacobian(transition_function)(self.state_predicted, control_input)
        self.covariance_predicted = transition_matrix \
                                        .dot(self.covariance_predicted) \
                                        .dot(transition_matrix.T) \
                                    + process_covariance

    def _update(self, observations_function: Callable[[np.array], np.array], observed: np.array,
                observations_covariance: np.matrix) -> None:
        measurement_residual = observed - observations_function(self.state_predicted)
        observations_matrix = nd.Jacobian(observations_function)(self.state_predicted)

        residual_covariance = observations_matrix \
                                  .dot(self.covariance_predicted) \
                                  .dot(observations_matrix.T) \
                              + observations_covariance
        kalman_gain = self.covariance_predicted.dot(observations_matrix.T).dot(residual_covariance.I)
        self.state_predicted += np.squeeze(np.asarray(kalman_gain.dot(measurement_residual)))
        self.covariance_predicted = (np.identity(kalman_gain.shape[0]) - kalman_gain.dot(observations_matrix))\
            .dot(self.covariance_predicted)

    def predict_update(self,
                       transition_function: Callable[[np.array, np.array], np.array],
                       observations_function: Callable[[np.array], np.array],
                       control_input: np.array,
                       observed: np.array,
                       process_covariance: np.matrix,
                       observations_covariance: np.matrix) -> Tuple[np.array, np.matrix]:
        self._predict(transition_function, control_input, process_covariance)
        self._update(observations_function, observed, observations_covariance)
        return self.state_predicted, self.covariance_predicted

4. 迭代扩展卡尔曼滤波 Iterative Extended Kalman Filter (IEKF)

IEKF 是在 EKF 上考虑了线性化误差的问题，EKF 的线性化点选择了在当前时刻的先验估计 $\check{\boldsymbol{x}}_k$ 进行。过程中线性化误差的会随着线性化点和工作点和差距而别大。因此一个很直观的想法是当我们通过这个线性化点得到当前时刻的后验估计 $\hat{\boldsymbol{x}}_k$ ，我们能不能以这个作为线性化点重新对观测模型进行线性化并重新估计当前时刻状态的后验分布。这个就是 IEKF 的思想。

大致上的流程就是先进行一次 EKF，得到第一次后验估计重复进行以下步骤：

$$\begin{aligned} \boldsymbol{x}_{op, k} &= \hat{\boldsymbol{x}}_k\\ \boldsymbol{z}_k &\approx \boldsymbol{z}_{op, k} + \boldsymbol{H}_{op, k}(\boldsymbol{x}_{k} - \boldsymbol{x}_{op, k}) + \boldsymbol{R}_k\boldsymbol{v}_k\\ \boldsymbol{K}_k &= (\check{\boldsymbol{P}}_k\boldsymbol{H}_{op, k}^T)(\boldsymbol{H}_{op, k}\check{\boldsymbol{P}}_k\boldsymbol{H}_{op, k}^T + \boldsymbol{R}\boldsymbol{V}\boldsymbol{R}^T)^{-1}\\ \hat{\boldsymbol{\mu}}_k = \hat{\boldsymbol{x}}_k &= \check{\boldsymbol{x}}_k + \boldsymbol{K}_k(\boldsymbol{z}_k - \boldsymbol{H}_{op, k}(\check{\boldsymbol{x}}_k-\boldsymbol{x}_{op,k}))\\ \hat{\boldsymbol{P}}_k &= (\boldsymbol{I} - \boldsymbol{K}_k\boldsymbol{H}_{op, k})\check{\boldsymbol{P}}_k \end{aligned}$$

class InvariantEKF:

    def __init__(self, system, mu_0, sigma_0):
        self.sys = system
        self.mus = [mu_0]
        self.sigmas = [sigma_0]
    def predict(self, u):
        #get mubar and sigmabar
        mu_bar, U = self.sys.f_lie(self.mu, u)
        adj_U = self.sys.adjoint(U)
        sigma_bar = adj_U @ self.sigma @ adj_U.T + self.sys.Q * self.sys.deltaT**2

        #save for use later
        self.mus.append( mu_bar )
        self.sigmas.append( sigma_bar )

        return mu_bar, sigma_bar

    def update(self, z):
        H = np.array([[0, 0, 0, 1, 0, 0, 0, 0, 0],
                      [0, 0, 0, 0, 1, 0, 0, 0, 0],
                      [0, 0, 0, 0, 0, 1, 0, 0, 0]])

        z = np.array([z[0], z[1], z[2], 1, 0])
        V = ( inv( self.mu )@z - self.sys.b )[:-2]

        invmu = inv(self.mu)[:3,:3]
        K = self.sigma @ H.T @ inv( H@self.sigma@H.T + invmu@self.sys.R@invmu.T )
        self.mus[-1] = self.mu @ expm( self.sys.carat(K @ V) )
        self.sigmas[-1] = (np.eye(9) - K @ H) @ self.sigma

        return self.mu, self.sigma

    def iterate(self, us, zs):
        for u, z in zip(us, zs):
            self.predict(u)
            self.update(z)

        return np.array(self.mus)[1:], np.array(self.sigmas)[1:]

5. 基于误差状态的卡尔曼滤波 Error State Extended Kalman Filter (ES-EKF)

…详情请参照古月居