卷积模型分类图片

1. 什么是卷积

卷积层是一组平行的特征图（feature map），它通过在输入图像上滑动不同的卷积核并运行一定的运算而组成。此外，在每一个滑动的位置上，卷积核与输入图像之间会运行一个元素对应乘积并求和的运算以将感受野内的信息投影到特征图中的一个元素。这一滑动的过程可称为步幅 ，步幅是控制输出特征图尺寸的一个因素。卷积核的尺寸要比输入图像小得多，且重叠或平行地作用于输入图像中，一张特征图中的所有元素都是通过一个卷积核计算得出的，也即一张特征图共享了相同的权重和偏置项。举个例子，有一张3*3的特征图，与2*2的卷积核进行卷积运算，得到的结果为一张2*2的特征图，运算过程如下图所示：

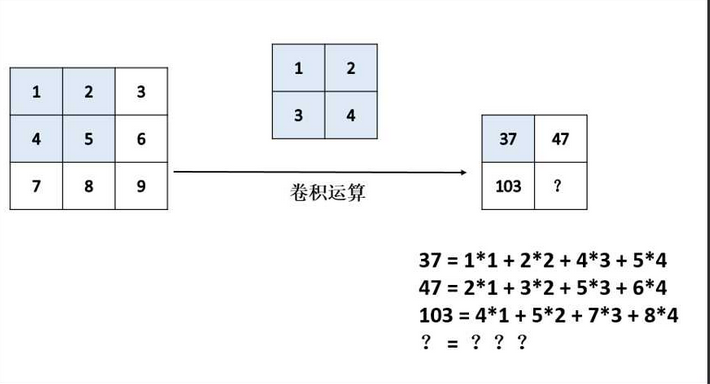
请问，你能将矩形框中的“？”补齐吗，答案是多少，动手算一算。

2. 卷积有什么用

卷积可以强调某些特征，然后将特征强化后提取出来，不同的卷积核关注图片上不同的特征，比如有的更关注边缘而有的更关注中心地带等等，可以设计不同的卷积核，实现我们想要的效果，如下图：

通过卷积，我们可以实现对原始图像的信息浓缩，以便于后续的处理。这也是为什么要使用卷积的原因之一。

2.1 通道的概念

在RGB色彩模式下，一张彩色的图片的通道数是3。分别为红色通道，绿色通道，和蓝色通道。卷积神经网络运算的中间阶段，一张图片的通道可能有很多，来看看下面这个例子：

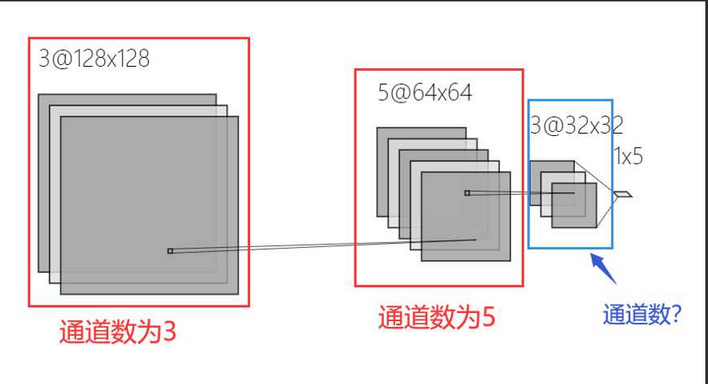
第一个红色框内通道数为3，它和我们常见的彩色图片通道数相同。第二个框的通道数为5，第三个蓝色框内特征图的通道数是多少呢？

2.2 理解滤波器（filter）的概念

卷积的时候是用多个‎filter‎完成的，一般经过卷积之后的输出（output shape ）的输入通道为filter的数量，下图为输入深度为2的操作，会发现一个filter的输出最终会相加，将它的深度压为1，而不是一开始的输入通道。这是一个filter，多个filter最后放在一起，最后的深度就是filter的数量了。

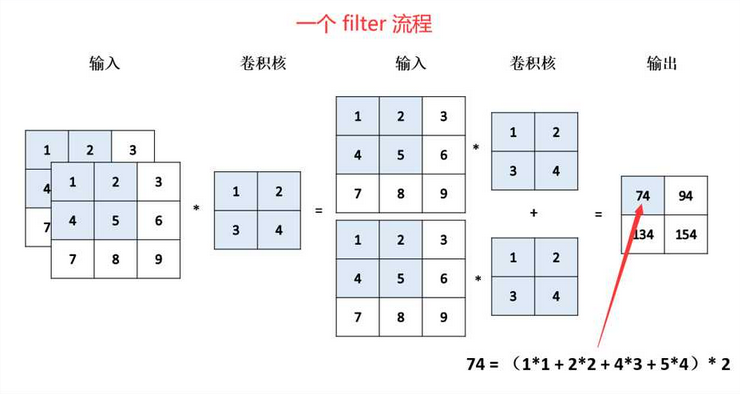
卷积核中的每一个参数，可以理解为连接神经元的权重。我们通过训练数据集让这些参数变得更加合理，从而使得模型的泛化预测能力更强。而为了实现这一过程，随着数据的增加，计算机的运算负荷也将增大，将计算数量控制在计算机可以承受的范围之内就需要对参数量有个大体的估计。具体的计算方法，感兴趣的小伙伴可以查阅相关资料，具体的计算方式不在此处展开。接下来我们搭建一个神经网络模型，对图片进行分类预测。

3. 卷积神经网络实例——图片10分类代码讲解

3.1 数据准备

导入相关库：

import tensorflow as tf

from tensorflow.keras import datasets, layers, models
import matplotlib.pyplot as plt

下载数据集：

(train_images, train_labels), (test_images, test_labels) = datasets.cifar10.load_data()

# 将像素的值标准化至0到1的区间内。
train_images, test_images = train_images / 255.0, test_images / 255.0

查看下载的数据集：

class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
               'dog', 'frog', 'horse', 'ship', 'truck']

plt.figure(figsize=(10,10))
for i in range(25):
    plt.subplot(5,5,i+1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    plt.imshow(train_images[i], cmap=plt.cm.binary)
    # 由于 CIFAR 的标签是 array， 
    # 因此您需要额外的索引（index）。
    plt.xlabel(class_names[train_labels[i][0]])
plt.show()

构建神经网络：

model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))

创建 密集层（Dense）/全连接层（Full Connected Layer)

model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10))

3.2 选择优化器和损失函数：

model.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
              metrics=['accuracy'])

3.3 训练模型：

history = model.fit(train_images, train_labels, epochs=10, 
                    validation_data=(test_images, test_labels))

3.4 评估模型：

plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0.5, 1])
plt.legend(loc='lower right')
plt.show()

test_loss, test_acc = model.evaluate(test_images,  test_labels, verbose=2)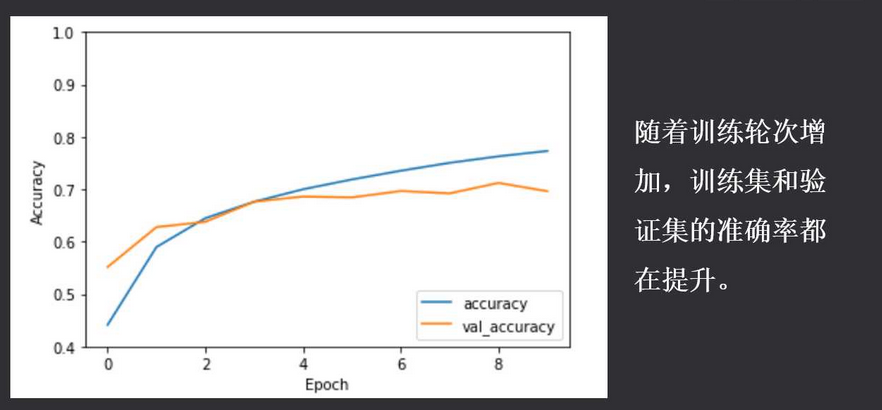

4. 拓展阅读

4.1 什么是过拟合

当存在少量训练示例时，模型有时会从训练示例中的噪声或不需要的细节中学习，从而对新示例的模型性能产生负面影响。这种现象被称为过度拟合。这意味着该模型将很难在新数据集上推广。具体表现为：当训练精度随时间线性增加，而验证精度在训练过程中停滞。在训练过程中，有多种方法可以防止过度拟合。下面介绍2种常见的方法，数据增广和Dropout操作。

4.2 数据增广 （data argumentation）

数据增广采用从现有示例生成额外训练数据的方法，方法是使用随机变换对其进行扩充，从而生成外观可信的图像。这有助于将模型学习到数据的更多方面，并更好地概括。

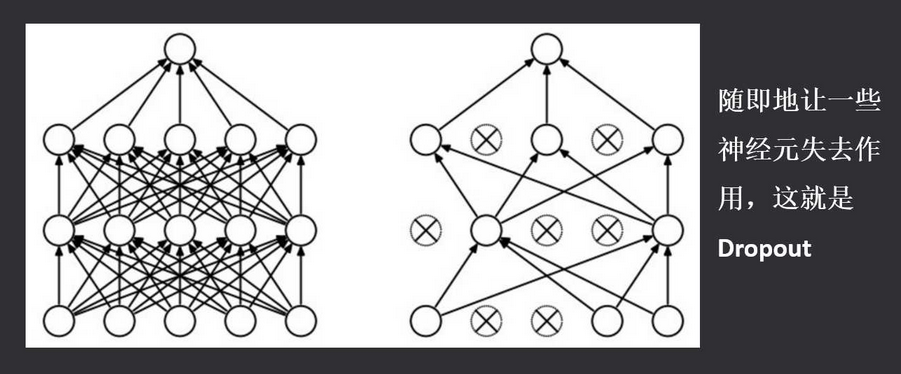
4.3 Dropout 操作

Dropout是Google提出的一种正则化技术，用以在人工神经网络中对抗过拟合。Dropout有效的原因，是它能够避免在训练数据上产生复杂的相互适应。Dropout这个术语代指在神经网络中丢弃部分神经元（包括隐藏神经元和可见神经元）。在训练阶段，dropout使得每次只有部分网络结构得到更新，因而是一种高效的神经网络模型平均化的方法。