一看就懂的单目特征点恢复深度信息(三角化)
【摘要】 0. 简介三角化作为SLAM中的基础问题,最近经常被提及,通过单目运动的方式可以有效的恢复深度信息 1. 线性三角化数学推导特征点在某个相机中被观测到,根据相机位姿和观测向量可以得到3D空间中的一条从相机中心出发的观测射线,多个相机位姿观测会产生多条观测射线,理想情况下这些观测射线会相交于空间中的一点,求所有观测射线的交点就是特征点在3D空间的位置,这也就是三角化过程。xxx,x′x'x′...
0. 简介
三角化作为SLAM中的基础问题,最近经常被提及,通过单目运动的方式可以有效的恢复深度信息
1. 线性三角化数学推导
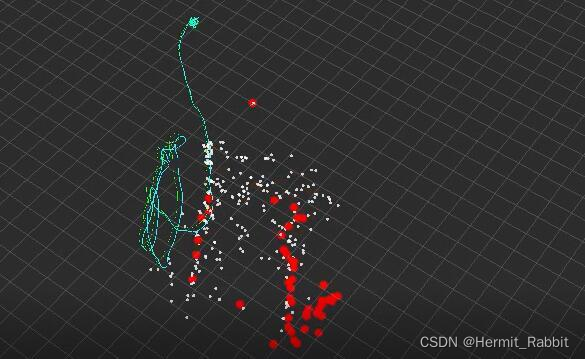
特征点在某个相机中被观测到,根据相机位姿和观测向量可以得到3D空间中的一条从相机中心出发的观测射线,多个相机位姿观测会产生多条观测射线,理想情况下这些观测射线会相交于空间中的一点,求所有观测射线的交点就是特征点在3D空间的位置,这也就是三角化过程。
,
为匹配特征点对
,
,
为投影矩阵
,
为空间中的三维点
,
为需要求解的深度值
此时式子1可以得到:
= 0
并根据矩阵差乘推出正交投影矩阵,因为 为常数,所以去除。
根据上式展开:
其中函数 中的第一行和第二行与第三行线性相关(通过第一行 ,第二行 ,再相加)。所以可以等效为:
此时的矩阵是一个匹配特征点
和一个投影矩阵
组成,而我们可以获得该
三维点的多个观测,此时可以根据多个观测构建出:
此时该方程为满秩
的,所以不存在非零解,此时使用SVD求解是惟一的
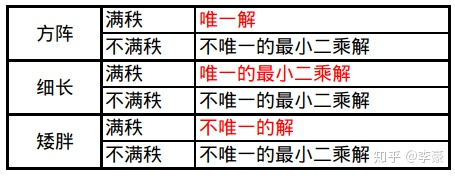
然后通过归一化保证结果为齐次坐标的
2. 常见的SLAM中的三角化代码
ORB-SLAM2
/*
* 三角化得到3D点
* *三角测量法 求解 两组单目相机 图像点深度
* s1 * x1 = s2 * R * x2 + t
* x1 x2 为两帧图像上 两点对 在归一化坐标平面上的坐标 k逆* p
* s1 和 s2为两个特征点的深度 ,由于误差存在, s1 * x1 = s2 * R * x2 + t不精确相等
* 常见的是求解最小二乘解,而不是零解
* s1 * x1叉乘x1 = s2 * x1叉乘* R * x2 + x1叉乘 t=0 可以求得x2
*
*/
/*
平面二维点摄影矩阵到三维点 P1 = K × [I 0] P2 = K * [R t]
kp1 = P1 * p3dC1 p3dC1 特征点匹配对 对应的 世界3维点
kp2 = P2 * p3dC1
kp1 叉乘 P1 * p3dC1 =0
kp2 叉乘 P2 * p3dC1 =0
p = ( x,y,1)
其叉乘矩阵为
// 叉乘矩阵 = [0 -1 y;
// 1 0 -x;
// -y x 0 ]
一个方程得到两个约束
对于第一行 0 -1 y; 会与P的三行分别相乘 得到四个值 与齐次3d点坐标相乘得到 0
有 (y * P.row(2) - P.row(1) ) * D =0
(-x *P.row(2) + P.row(0) ) * D =0 ===> (x *P.row(2) - P.row(0) ) * D =0
两个方程得到 4个约束
A × D = 0
对A进行奇异值分解 求解线性方程 得到 D (D是3维齐次坐标,需要除以第四个尺度因子 归一化)
*/
// Trianularization: 已知匹配特征点对{x x'} 和 各自相机矩阵{P P'}, 估计三维点 X
// x' = P'X x = PX
// 它们都属于 x = aPX模型
// |X|
// |x| |p1 p2 p3 p4 ||Y| |x| |--p0--||.|
// |y| = a |p5 p6 p7 p8 ||Z| ===>|y| = a|--p1--||X|
// |z| |p9 p10 p11 p12||1| |z| |--p2--||.|
// 采用DLT的方法:x叉乘PX = 0
// |yp2 - p1| |0|
// |p0 - xp2| X = |0|
// |xp1 - yp0| |0|
// 两个点:
// |yp2 - p1 | |0|
// |p0 - xp2 | X = |0| ===> AX = 0
// |y'p2' - p1' | |0|
// |p0' - x'p2'| |0|
// 变成程序中的形式:
// |xp2 - p0 | |0|
// |yp2 - p1 | X = |0| ===> AX = 0
// |x'p2'- p0'| |0|
// |y'p2'- p1'| |0|
/**
* @brief 给定投影矩阵P1,P2和图像上的点kp1,kp2,从而恢复3D坐标
*
* @param kp1 特征点, in reference frame
* @param kp2 特征点, in current frame
* @param P1 投影矩阵P1
* @param P2 投影矩阵P2
* @param x3D 三维点
* @see Multiple View Geometry in Computer Vision - 12.2 Linear triangulation methods p312
*/
void Initializer::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
{
// 在DecomposeE函数和ReconstructH函数中对t有归一化
// 这里三角化过程中恢复的3D点深度取决于 t 的尺度,
// 但是这里恢复的3D点并没有决定单目整个SLAM过程的尺度
// 因为CreateInitialMapMonocular函数对3D点深度会缩放,然后反过来对 t 有改变
cv::Mat A(4,4,CV_32F);
A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);
cv::Mat u,w,vt;
cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
x3D = vt.row(3).t();
x3D = x3D.rowRange(0,3)/x3D.at<float>(3);// 转换成非齐次坐标 归一化
}
VINS-Mono
…详情请参照古月居
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)