0. 简介

作为主流框架的前端中常用的方法，划窗优化是很常见迭代策略。因为随着SLAM系统的运行，状态变量规模不断增大，如果使用滑动窗口，只对窗口内的相关变量进行优化便可以大大减小计算量。这些之前在我的博客中有提到，但是之前作者没有深入的去了解这些，只是对边缘化中的舒尔补策略进行了简略的介绍。

而作为划窗优化，我们除了创建滑动窗口的存储空间外，我们还要通过边缘化的方法保留滑窗外的状态，我们可以不去优化划窗外的参数，但也不能直接丢掉，这样会破坏原有的约束关系，损失约束信息。采用边缘化的技巧，将约束信息转化为待优化变量的先验分布，实际上是一个从联合分布中获得变量子集概率分布的问题。

1. 划窗优化的操作步骤

以vins系统为代表，其中和边缘化优化相关的代码存放在下列文件中：

1）vins_estimator/src/factor/marginalization_factor.cpp：边缘化的具体实现

2）vins_estimator/src/estimator.cpp（部分）：

函数optimization负责利用边缘化残差构建优化模型
函数slideWindow负责维护滑动窗口

解释了这三个问题，我们其实就完成了理解VINS-Mono里这个问题的理论部分，下面看代码实践部分。

2. 边缘化的具体实现

2.1 特征提取

这里我们以地图定位滑动窗口模型为例，来介绍特征提取匹配模型的建立。

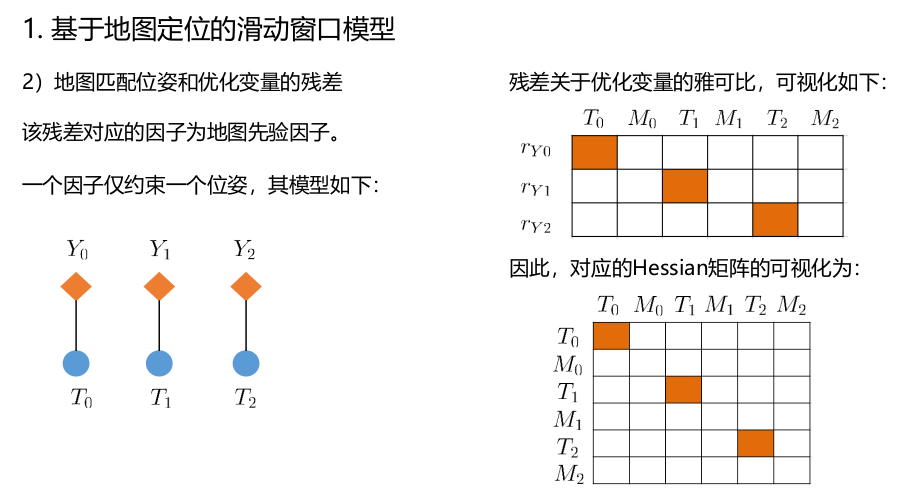
地图匹配因子的残差函数和雅克比矩阵推导如下图：

其中residual.block对应了上图中的residual变量，而由于上图中表明一个地图定位表示一个定位点，所以 $r_p$等于预测向量与观测相量的误差， $r_q$通过计算预测旋转量 $R$和观测相量 $R_{obs}$的差值，并通过BCH将李群转为李代数，从而得到一个一阶近似的李代数。
在上面的求导过程中第一步为求导： ${r_q}的{R}偏导数格式为{[R*ln(exp(\phi)*{R_obs}) - ln(R*{R_obs}) ]/{\phi}}$，如果R为转置，则为： ${[ln(exp(\phi)*R*{R_obs}) - ln(R*{R_obs}) ]/{\phi}}$

第二步和第三步则是通过扩充 $R_obs$和其转置然后置换成 $R*{R_obs}$形式，并根据李代数的伴随性质，得到式子3的结果（利用ln乘法变加法的原则），并BCH近似得到式子4.

    //
    // TODO: get square root of information matrix:
    //
    // Cholesky 分解 : http://eigen.tuxfamily.org/dox/classEigen_1_1LLT.html
    Eigen::Matrix<double, 6, 6> sqrt_info = Eigen::LLT<Eigen::Matrix<double, 6, 6>>(
      I_
    ).matrixL().transpose();

    //
    // TODO: compute residual:
    //
    Eigen::Map<Eigen::Matrix<double, 6 ,1>>  residual(residuals);

              residual.block(INDEX_P, 0 , 3 , 1 )   =  pos - pos_prior ;
              residual.block(INDEX_R,0 , 3 , 1 )    = (ori*ori_prior.inverse()).log();
    //
    // TODO: compute jacobians:   一元边
    //
    if ( jacobians ) {
      if ( jacobians[0] ) {
        // implement jacobian computing:
        Eigen::Map<Eigen::Matrix<double, 6, 15,  Eigen::RowMajor>> jacobian_prior(jacobians[0] );
        jacobian_prior.setZero();

        jacobian_prior.block<3, 3>(INDEX_P,  INDEX_P) = Eigen::Matrix3d::Identity();
        jacobian_prior.block<3, 3>(INDEX_R, INDEX_R)  = JacobianRInv(
                                  residual.block(INDEX_R, 0, 3, 1)) * ori_prior.matrix();
        
        jacobian_prior = sqrt_info * jacobian_prior ;
      }
    }

2.2 ceres优化调用（本质是第三点内容，这里先提一下，方便连贯）

ceres优化求解，保存优化参数块结果，并压入到边缘化中

 // 只有第1个预积分和待边缘化参数块相连
 {
     if (pre_integrations[1]->sum_dt < 10.0)
     {
         // 跟构建ceres约束问题一样，这里也需要得到残差和雅克比
         IMUFactor* imu_factor = new IMUFactor(pre_integrations[1]);
         ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(imu_factor, NULL,
                                                                    vector<double *>{para_Pose[0], para_SpeedBias[0], para_Pose[1], para_SpeedBias[1]},
                                                                    vector<int>{0, 1});  // 这里就是第0和1个参数块是需要被边缘化的
         marginalization_info->addResidualBlockInfo(residual_block_info);
     }
 }

2.3 添加残差块信息

上面展示的是每一块待优化变量的优化变量，而其实我们存在有很多残差块，vins中就有一部分是用来添加残差块相关信息（优化变量，待边缘化变量）

void MarginalizationInfo::addResidualBlockInfo(ResidualBlockInfo *residual_block_info)
{
    factors.emplace_back(residual_block_info);  // 残差块收集起来

    std::vector<double *> &parameter_blocks = residual_block_info->parameter_blocks;    // 这个是和该约束相关的参数块
    std::vector<int> parameter_block_sizes = residual_block_info->cost_function->parameter_block_sizes();   // 各个参数块的大小

    for (int i = 0; i < static_cast<int>(residual_block_info->parameter_blocks.size()); i++)
    {
        double *addr = parameter_blocks[i];
        int size = parameter_block_sizes[i];
        // 这里是个map，避免重复添加
        parameter_block_size[reinterpret_cast<long>(addr)] = size;  // 地址->global size
    }
    // 待边缘化的参数块
    for (int i = 0; i < static_cast<int>(residual_block_info->drop_set.size()); i++)
    {
        double *addr = parameter_blocks[residual_block_info->drop_set[i]];
        // 先准备好待边缘化的参数块的map
        parameter_block_idx[reinterpret_cast<long>(addr)] = 0;
    }
}

2.4 preMarginalize：更新参数块

将各个残差块计算残差和雅克比，同时备份所有相关的参数块内容，并更新parameter_block_data

void MarginalizationInfo::preMarginalize()
{
    for (auto it : factors)
    {
        it->Evaluate(); // 调用这个接口计算各个残差块的残差和雅克比矩阵

        std::vector<int> block_sizes = it->cost_function->parameter_block_sizes();  // 得到每个残差块的参数块大小
        for (int i = 0; i < static_cast<int>(block_sizes.size()); i++)
        {
            long addr = reinterpret_cast<long>(it->parameter_blocks[i]);    // 得到该参数块的地址
            int size = block_sizes[i];  // 参数块大小
            // 把各个参数块都备份起来，使用map避免重复参数块，之所以备份，是为了后面的状态保留
            if (parameter_block_data.find(addr) == parameter_block_data.end())
            {
                double *data = new double[size];
                // 深拷贝
                memcpy(data, it->parameter_blocks[i], sizeof(double) * size);
                parameter_block_data[addr] = data;  // 地址->参数块实际内容的地址
            }
        }
    }
}

2.4. marginalize：执行边缘化

多线程构造先验项舒尔补AX=b的结构，边缘化处理，并将结果转换成残差和雅克比的形式

void MarginalizationInfo::marginalize()
{
    int pos = 0;
    // parameter_block_idx key是各个待边缘化参数块地址 value预设都是0
    for (auto &it : parameter_block_idx)
    {
        it.second = pos;    // 这就是在所有参数中排序的idx，待边缘化的排在前面
        pos += localSize(parameter_block_size[it.first]);   // 因为要进行求导，因此大小时local size，具体一点就是使用李代数
    }

    m = pos;    // 总共待边缘化的参数块总大小（不是个数）
    // 其他参数块
    for (const auto &it : parameter_block_size)
    {
        if (parameter_block_idx.find(it.first) == parameter_block_idx.end())
        {
            parameter_block_idx[it.first] = pos;    // 这样每个参数块的大小都能被正确找到
            pos += localSize(it.second);
        }
    }

    n = pos - m;    // 其他参数块的总大小

    //ROS_DEBUG("marginalization, pos: %d, m: %d, n: %d, size: %d", pos, m, n, (int)parameter_block_idx.size());

    TicToc t_summing;
    Eigen::MatrixXd A(pos, pos);    // Ax = b预设大小
    Eigen::VectorXd b(pos);
    A.setZero();
    b.setZero();
    /*
    for (auto it : factors)
    {
        for (int i = 0; i < static_cast<int>(it->parameter_blocks.size()); i++)
        {
            int idx_i = parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[i])];
            int size_i = localSize(parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[i])]);
            Eigen::MatrixXd jacobian_i = it->jacobians[i].leftCols(size_i);
            for (int j = i; j < static_cast<int>(it->parameter_blocks.size()); j++)
            {
                int idx_j = parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[j])];
                int size_j = localSize(parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[j])]);
                Eigen::MatrixXd jacobian_j = it->jacobians[j].leftCols(size_j);
                if (i == j)
                    A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
                else
                {
                    A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
                    A.block(idx_j, idx_i, size_j, size_i) = A.block(idx_i, idx_j, size_i, size_j).transpose();
                }
            }
            b.segment(idx_i, size_i) += jacobian_i.transpose() * it->residuals;
        }
    }
    ROS_INFO("summing up costs %f ms", t_summing.toc());
    */
    //multi thread

    // 往A矩阵和b矩阵中填东西，利用多线程加速
    TicToc t_thread_summing;
    pthread_t tids[NUM_THREADS];
    ThreadsStruct threadsstruct[NUM_THREADS];
    int i = 0;
    for (auto it : factors)
    {
        threadsstruct[i].sub_factors.push_back(it); // 每个线程均匀分配任务
        i++;
        i = i % NUM_THREADS;
    }
    // 每个线程构造一个A矩阵和b矩阵，最后大家加起来
    for (int i = 0; i < NUM_THREADS; i++)
    {
        TicToc zero_matrix;
        // 所以A矩阵和b矩阵大小一样，预设都是0
        threadsstruct[i].A = Eigen::MatrixXd::Zero(pos,pos);
        threadsstruct[i].b = Eigen::VectorXd::Zero(pos);
        // 多线程访问会带来冲突，因此每个线程备份一下要查询的map
        threadsstruct[i].parameter_block_size = parameter_block_size;   // 大小
        threadsstruct[i].parameter_block_idx = parameter_block_idx; // 索引
        // 产生若干线程
        int ret = pthread_create( &tids[i], NULL, ThreadsConstructA ,(void*)&(threadsstruct[i]));
        if (ret != 0)
        {
            ROS_WARN("pthread_create error");
            ROS_BREAK();
        }
    }
    for( int i = NUM_THREADS - 1; i >= 0; i--)  
    {
        // 等待各个线程完成各自的任务
        pthread_join( tids[i], NULL );
        // 把各个子模块拼起来，就是最终的Hx = g的矩阵了 
        A += threadsstruct[i].A;
        b += threadsstruct[i].b;
    }
    //ROS_DEBUG("thread summing up costs %f ms", t_thread_summing.toc());
    //ROS_INFO("A diff %f , b diff %f ", (A - tmp_A).sum(), (b - tmp_b).sum());


    // Amm矩阵的构建是为了保证其正定性，从而确保迭代的稳定性
    Eigen::MatrixXd Amm = 0.5 * (A.block(0, 0, m, m) + A.block(0, 0, m, m).transpose());
    // 检查矩阵是否是self-adjoint。SelfAdjointEigenSolver 可以通过EigenSolver或者ComplexEigenSolver方法适用于一般矩阵
    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);   // 特征值分解

    //ROS_ASSERT_MSG(saes.eigenvalues().minCoeff() >= -1e-4, "min eigenvalue %f", saes.eigenvalues().minCoeff());
    // 一个逆矩阵的特征值是原矩阵的倒数，特征向量相同　select类似c++中 ? :运算符
    // 利用特征值取逆来构造其逆矩阵
    Eigen::MatrixXd Amm_inv = saes.eigenvectors() * Eigen::VectorXd((saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal() * saes.eigenvectors().transpose();
    //printf("error1: %f\n", (Amm * Amm_inv - Eigen::MatrixXd::Identity(m, m)).sum());
   



	 // 线性化残差 和 雅克比
    Eigen::VectorXd bmm = b.segment(0, m);  // 带边缘化的大小
    Eigen::MatrixXd Amr = A.block(0, m, m, n);  // 对应的四块矩阵
    Eigen::MatrixXd Arm = A.block(m, 0, n, m);
    Eigen::MatrixXd Arr = A.block(m, m, n, n);
    Eigen::VectorXd brr = b.segment(m, n); // 剩下的参数
    A = Arr - Arm * Amm_inv * Amr;
    b = brr - Arm * Amm_inv * bmm;

    // 这个地方根据Ax = b => JT*J = - JT * e
    // 对A做特征值分解 A = V * S * VT,其中Ｓ是特征值构成的对角矩阵
    // 所以J = S^(1/2) * VT , 这样JT * J = (S^(1/2) * VT)T * S^(1/2) * VT = V * S^(1/2)T *  S^(1/2) * VT = V * S * VT(对角矩阵的转置等于其本身)
    // e = -(JT)-1 * b = - (S^-(1/2) * V^-1) * b = - (S^-(1/2) * VT) * b
    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);
    // 对A矩阵取逆
    Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
    Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));

    Eigen::VectorXd S_sqrt = S.cwiseSqrt(); // 这个求得就是 S^(1/2)，不过这里是向量还不是矩阵
    Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();
    // 边缘化为了实现对剩下参数块的约束，为了便于一起优化，就抽象成了残差和雅克比的形式，这样也形成了一种残差约束
    linearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();
    linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().transpose() * b;
    //std::cout << A << std::endl
    //          << std::endl;
    //std::cout << linearized_jacobians << std::endl;
    //printf("error2: %f %f\n", (linearized_jacobians.transpose() * linearized_jacobians - A).sum(),
    //      (linearized_jacobians.transpose() * linearized_residuals - b).sum());
}

3. optimization：负责边缘化残差的使用

这个函数位于vins_estimator/src/estimator.cpp文件中，而且它负责整个系统所有的优化工作，边缘化残差的使用只是它功能的一部分。

3.1 定义待优化的参数块

Step 1 定义待优化的参数块，类似g2o的顶点

// 参数块 1： 滑窗中位姿包括位置和姿态，共11帧
    for (int i = 0; i < WINDOW_SIZE + 1; i++)
    {
        // 由于姿态不满足正常的加法，也就是李群上没有加法，因此需要自己定义他的加法
        ceres::LocalParameterization *local_parameterization = new PoseLocalParameterization();
        problem.AddParameterBlock(para_Pose[i], SIZE_POSE, local_parameterization);
        problem.AddParameterBlock(para_SpeedBias[i], SIZE_SPEEDBIAS);
    }
    // 参数块 2： 相机imu间的外参
    for (int i = 0; i < NUM_OF_CAM; i++)
    {
        ceres::LocalParameterization *local_parameterization = new PoseLocalParameterization();
        problem.AddParameterBlock(para_Ex_Pose[i], SIZE_POSE, local_parameterization);
        if (!ESTIMATE_EXTRINSIC)
        {
            ROS_DEBUG("fix extinsic param");
            // 如果不需要优化外参就设置为fix
            problem.SetParameterBlockConstant(para_Ex_Pose[i]);
        }
        else
            ROS_DEBUG("estimate extinsic param");
    }

3.2 添加边缘化残差

Step 2 通过残差约束来添加残差块，类似g2o的边

    //上一次的边缘化结果作为这一次的先验
    if (last_marginalization_info)
    {
        // construct new marginlization_factor
        MarginalizationFactor *marginalization_factor = new MarginalizationFactor(last_marginalization_info);
        problem.AddResidualBlock(marginalization_factor, NULL,
                                 last_marginalization_parameter_blocks);
    }
    // imu预积分的约束
    for (int i = 0; i < WINDOW_SIZE; i++)
    {
        int j = i + 1;
        // 时间过长这个约束就不可信了
        if (pre_integrations[j]->sum_dt > 10.0)
            continue;
        IMUFactor* imu_factor = new IMUFactor(pre_integrations[j]);
        problem.AddResidualBlock(imu_factor, NULL, para_Pose[i], para_SpeedBias[i], para_Pose[j], para_SpeedBias[j]);
    }
..........

3.3 ceres 优化求解并得到结果

// Step 3 ceres优化求解
    ceres::Solver::Options options;

    options.linear_solver_type = ceres::DENSE_SCHUR;
    //options.num_threads = 2;
    options.trust_region_strategy_type = ceres::DOGLEG;
    options.max_num_iterations = NUM_ITERATIONS;
    //options.use_explicit_schur_complement = true;
    //options.minimizer_progress_to_stdout = true;
    //options.use_nonmonotonic_steps = true;
    if (marginalization_flag == MARGIN_OLD)
        // 下面的边缘化老的操作比较多，因此给他优化时间就少一些
        options.max_solver_time_in_seconds = SOLVER_TIME * 4.0 / 5.0;
    else
        options.max_solver_time_in_seconds = SOLVER_TIME;
    TicToc t_solver;
    ceres::Solver::Summary summary;
    ceres::Solve(options, &problem, &summary);  // ceres优化求解
    //cout << summary.BriefReport() << endl;
    ROS_DEBUG("Iterations : %d", static_cast<int>(summary.iterations.size()));
    ROS_DEBUG("solver costs: %f", t_solver.toc());
    // 把优化后double -> eigen
    double2vector();

3.4 边缘化策略

边缘化分两种情况，每种情况有各自的流程

a. 如果次新帧是关键帧，则将边缘化最老帧，及其看到的路标点和IMU数据，转化为先验。具体流程为：

1）将上一次先验残差项传递给marginalization_info

2）将第0帧和第1帧间的IMU因子IMUFactor(pre_integrations[1])，添加到marginalization_info中

3）将第一次观测为第0帧的所有路标点对应的视觉观测，添加到marginalization_info中

4）计算每个残差，对应的Jacobian，并将各参数块拷贝到统一的内存（parameter_block_data）中

5）多线程构造先验项舒尔补AX=b的结构，在X0处线性化计算Jacobian和残差

6）调整参数块在下一次窗口中对应的位置（往前移一格），注意这里是指针，后面slideWindow中会赋新值，这里只是提前占座

b. 如果次新帧不是关键帧，此时具体流程为：

1）保留次新帧的IMU测量，丢弃该帧的视觉测量，将上一次先验残差项传递给marginalization_info

2）premargin：计算每个残差，对应的Jacobian，并更新parameter_block_data

3）marginalize：构造先验项舒尔补AX=b的结构，计算Jacobian和残差

4）调整参数块在下一次窗口中对应的位置（去掉次新帧）

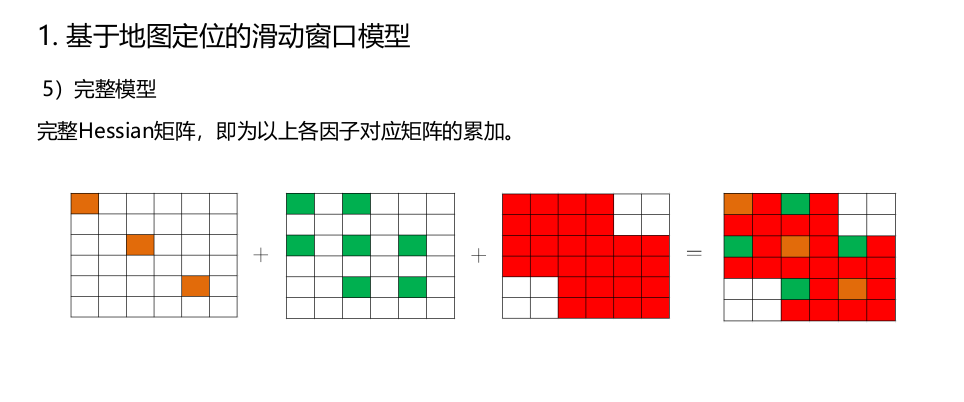
…详情请参照古月居