信息论与编码（二）| 自信息与信息熵

自信息

信息量

如何考察或计算信源输出的消息(或者符号)的信息量?

• 信源的信息实质:不确定性（信源输出的是消息，消息的内涵是信息。信源输出一个符号，我们认为发生一个事件）。
• 数学上我们用概率（或概率密度）来表征事件不确定性的大小。

1.信息量的大小与不确定性的消除多少有关;

收到某消息获得的信息量=不确定性的减少量=(收到该消息前关于某事件发生的不确定性)-(收到此消息后关于某事件发生的不确定性)

2.信道无噪声，收到某消息获得的信息量=收到该消息前关于某事件发生的不确定性=信源输出的某消息中所含的信息量。

3.概率小→不确定性大;概率大→不确定性小。

因此，某事件发生所含的信息量应该是该事件发生的先验概率的函数。

自信息定义

事件集合 $\mathbf{X}$ 中的事件 $\mathrm{x}=\mathrm{x}_{\mathbf{i}}$ 的自信息定义为 $I_{X}\left(x_{i}\right)=-\log p_{X}\left(x_{i}\right)$ 或记为: $I(x)=-\log p(x)$

注意 1 : 要求 $I(x)$ 非负. 所以对数的底数必须大于 1 .

• 底数为 2 , 单位为比特 (bit) ;
• 底数为 $\mathrm{e}$ , 单位为奈特 (Nat)；
• 底数为 10 , 单位为笛特(Det)。

1 bit =0.693 Nat =0.301 Det

注意2: I(x) 是随机变量.

自信息的含义:

• 在事件发生前, 自信息表示事件发生的不确定性。
• 在事件发生后, 自信息表示事件所包含的信息量, 是提供给信宿的信息量, 也是解除这种不确定性所需要的信息量

联合自信息

联合事件集合 $\mathbf{X Y}$ 中的事件 $x=x_{i}, y=y_{j}$ 的自信息定义为

$\begin{array}{l} I_{X Y}\left(x_{i} y_{j}\right)=-\log P X\left(x_{i} y_{j}\right) \text { or } I(x y) \\ =-\log p(x y) \end{array}$

其中, $p(x y)$ 要满足非负和归一化的条件。

条件自信息

事件 $\mathbf{x}=\mathbf{x}_{\mathbf{i}}$ 在事件 $\mathbf{y}=\mathbf{y}_{\mathbf{j}}$ 给定条件下的自信息定义为

$I_{X \mid Y}\left(x_{i} \mid y_{j}\right)=-\log P_{X \mid Y}\left(x_{i} \mid y_{j}\right)$or $I(x \mid y)=-\log p(x \mid y) $
-条件自信息的含义
-在事件 $y=y_{j}$ 给定条件下, 在 $x=x_{i}$ 发生前的不 确定性;
-在事件 $y=y_{j}$ 给定条件下, 在 $x=x_{i}$ 发生后所得到的信息量。

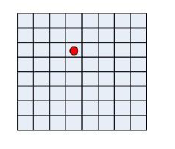
Example 3有8×8=64个方格，甲将一棋子放入方格中，让乙猜。
1、将方格顺序编号，让乙猜顺序号的难度程度如何?
2、将方格按行和列编号，当甲告诉乙方格的行号后，让乙猜列顺序号的难度如何?

-解：两种情况的不确定性:

$\begin{array}{l} I(x y)=\log _{2} 64=6 b i t \\ I(x \mid y)=-\log _{2} p(x \mid y)=\log _{2}(1 / 8)=3 \text { bit } \end{array}$

信息熵

信源符号自信息的数学期望为信源的平均信息量一信息熵

$H(X)=E\left(I\left(X_{i}\right)\right)=-\sum_{i=1}^{N} p_{i} \log p_{i} \quad bit/symbol$

注意: $\mathbf{H}(\mathbf{X})$ 是一个数, 不是随机变量.

Example 3 请计算下述离散无记忆二进制信源的信息熵。
Solution

$\begin{array}{l} \left(\begin{array}{l} X \\ p \end{array}\right)=\left(\begin{array}{cc} 0 & 1 \\ p & 1-p \end{array}\right) \\ H(X)=-p \log p-(1-p) \log (1-p) \end{array}$

信息熵的物理含义

1.信息熵H(X)表示信源输出后，每个消息（符号）所提供的平均信息量;

2.信息熵H(X)表示信源输出前，信源的平均不确定性;

3.用信息熵H(X)来表征变量X的随机性。

注:信息熵不等于平均获得的信息量。一般情况下获得的信息量是两熵之差，而不是信息熵本身。

Example4:

甲地天气预报， $\left[\begin{array}{c}X \\ p(X)\end{array}\right]=\left[\begin{array}{cccc}\text { 晴 阴 雨 雪 } \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{8} & \frac{1}{8}\end{array}\right]$
乙地天气预报 $\left[\begin{array}{c}Y \\ p(Y)\end{array}\right]=\left[\begin{array}{cc}\text { 晴 } & \text { 雨 } \\ \frac{7}{8} & \frac{1}{8}\end{array}\right]$
求：两地天气预报各自提供的平均信息量

解:

• $\mathrm{H}(\mathrm{X})=-\frac{1}{2} \log \frac{1}{2}-\frac{1}{4} \log \frac{1}{4}-\frac{1}{8} \log \frac{1}{8}-\frac{1}{8} \log \frac{1}{8}=1.75 \quad$ 比特/符号
• $\mathrm{H}(\mathrm{Y})=-\frac{7}{8} \log \frac{7}{8}-\frac{1}{8} \log \frac{1}{8}=0.544 \quad$ 比特/符号 甲地提供的平均信息量大于乙地。

甲、乙地天气预报为两极端情况:

$\left[\begin{array}{l} X \\ p(x) \end{array}\right]=\left[\begin{array}{cccc} \text { 晴 } & \text { 阴 } & \text { 雨 } & \text { 雪 } \\ 1 & 0 & 0 & 0 \end{array}\right] \quad\left[\begin{array}{l} \mathrm{Y} \\ \mathrm{p}(\mathrm{y}) \end{array}\right]=\left[\begin{array}{cc} \text { 晴 } & \text { 雨 } \\ 1 & 0 \end{array}\right]$

$\mathrm{H}(\mathrm{X})=-1 \log 1-0 \log 0-0 \log 0-0 \log 0=0 比特/符号 $

$\mathrm{H}(\mathrm{Y})=-1 \log 1-0 \log 0=0$ 比特/符号
$\lim \varepsilon \log \varepsilon=0$

• 信源是确定信源, 所以不存在不确定性, 信息熵等于零。

甲、乙地天气预报为两极端情况:
$\left[\begin{array}{c}X \\ p(x)\end{array}\right]=\left[\begin{array}{cccc}\text { 晴 } & \text { 阴 } & \text { 雨 } & \text { 雪 } \\ 1 / 4 & 1 / 4 & 1 / 4 & 1 / 4\end{array}\right] \quad\left[\begin{array}{l}\mathrm{Y} \\ \mathrm{p}(\mathrm{y})\end{array}\right]=\left[\begin{array}{cc}\text { 哇, } & \text { 雨 } \\ 1 / 2 & 1 / 2\end{array}\right] \mathrm{H}(\mathrm{X})=-\log \frac{1}{4}=2 比特/符号$
$ H(Y)=-\log \frac{1}{2}=1$ 比特/符号

• 这种情况下,信源的不确定性最大,信息熵最大。
• 甲地比乙地提供更多的信息量。因为甲地可能出现的消 息数多于て地可能出现的消息数, 不确定性更大。

结论: 信源熵大于等于0（若信源输出为确定符号)而小于等于log(N)（信源输出的不确定性最大)。
$0≤H(X)≤ log(N)$
其中N为信源字符集元素的个数

Example 5 某信号带宽为4000Hz ，以奈奎斯特速率抽样。假设其抽样序列可以建模成一个字符集为A={-2,-1,0,1,2}的DMS，相应的概率为{1/2,1/4,1/8,1/16,1/16},求信源的速率(b/s)

$H(X)=\frac{1}{2} \log 2+\frac{1}{4} \log 4+\frac{1}{8} \log 8+2 \times \frac{1}{16} \log 16$

$=\frac{15}{8} \quad \mathrm{bit} / \mathrm{symbol} R_{b}=2 \times 4000 \times H(X)=15 K bit / \mathrm{sec}$
其中 $R_{\mathrm{b}}$ 为信息速率。
注：奈奎斯特抽样速率为 $2 \mathbf{W}$ 。