Unity【Bounds & Vector3 Cross】- 如何判断一个物体是否在一个凸边体三维区域内
如图所示,本文介绍如何判断一个物体是否被一个凸边体区域所囊括,本文将该功能的实现拆分成了如下步骤:
1.如何判断两条线段是否相交
2.如何判断一个点是否在一个凸边形范围内(2D、xz轴构成的平面)
3.如何判断一个点是否在一个凸边体范围内(3D)
4.如何判断一个物体是否在一个凸边体范围内
依次实现:
1.如何判断两条线段是否相交:
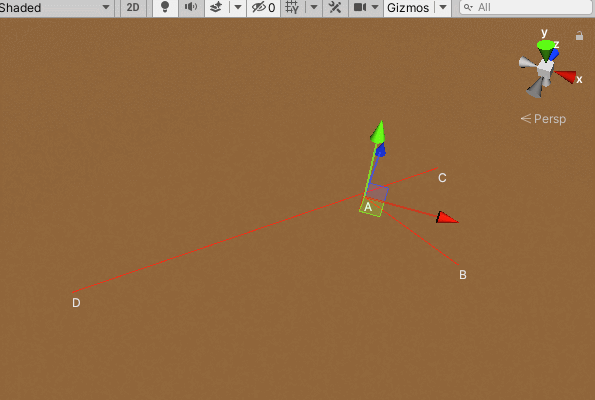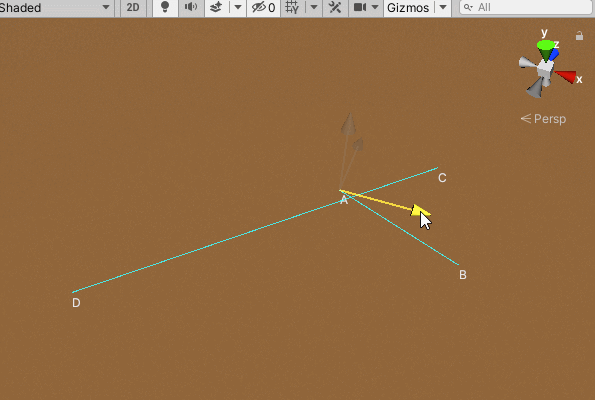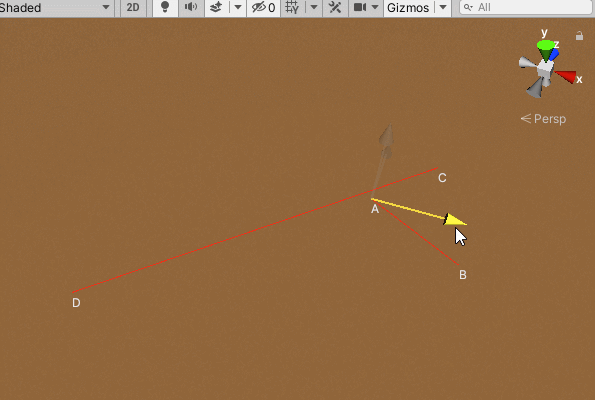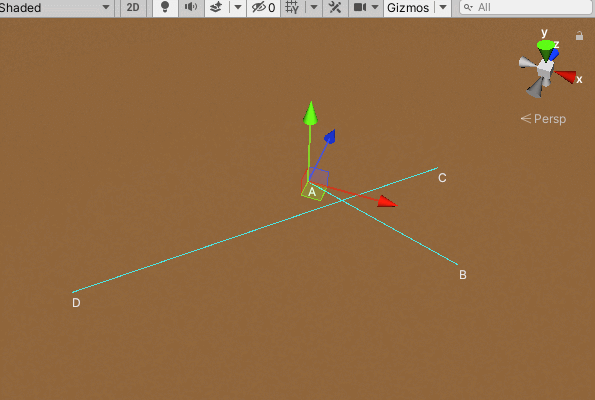
通过矢量叉积的符号可以判断两矢量相互之间的顺逆时针关系,如下图所示,点A和点B分别在线段CD两侧,点C和点D分别在线段AB两侧,这时可以判断它们相交。判断点A和点B是否在线段CD两侧,也就是判断向量A-D和向量B-D在向量C-D的两侧,也就是叉积的结果是异号的,即:(A-D)X(C-D)*(B-D)X(C-D)< 0。同样的,判断点C和点B是否在线段AB的两侧:(D-A)X(B-A)*(C-A)X(B-A)< 0,以上这两个条件成立时,可判断两线段相交。

当然,出现以下这种情况,即(A-D)X(C-D)*(B-D)X(C-D)= 0时,两条线段也是相交的:

在Unity中封装该判断函数:
//判断AB与CD是否相交
private bool IsIntersection(Vector3 A, Vector3 B, Vector3 C, Vector3 D)
{
//A-D与C-D叉积结果大等于0时返回1 小于0时返回-1
float sign1 = Mathf.Sign(Vector3.Cross(A - D, C - D).y);
//B-D与C-D叉积结果大等于0时返回1 小于0时返回-1
float sign2 = Mathf.Sign(Vector3.Cross(B - D, C - D).y);
//C-A与B-A叉积结果大等于0时返回1 小于0时返回-1
float sign3 = Mathf.Sign(Vector3.Cross(C - A, B - A).y);
//D-A与B-A叉积结果大等于0时返回1 小于0时返回-1
float sign4 = Mathf.Sign(Vector3.Cross(D - A, B - A).y);
//AB与CD相交返回true 否则返回false
return !Mathf.Approximately(sign1, sign2) && !Mathf.Approximately(sign3, sign4);
} 
测试脚本如下:
using UnityEngine;
using UnityEditor;
public class Example : MonoBehaviour
{
[SerializeField] private Transform a;
[SerializeField] private Transform b;
[SerializeField] private Transform c;
[SerializeField] private Transform d;
//判断AB与CD是否相交
private bool IsIntersection(Vector3 A, Vector3 B, Vector3 C, Vector3 D)
{
//A-D与C-D叉积结果大等于0时返回1 小于0时返回-1
float sign1 = Mathf.Sign(Vector3.Cross(A - D, C - D).y);
//B-D与C-D叉积结果大等于0时返回1 小于0时返回-1
float sign2 = Mathf.Sign(Vector3.Cross(B - D, C - D).y);
//C-A与B-A叉积结果大等于0时返回1 小于0时返回-1
float sign3 = Mathf.Sign(Vector3.Cross(C - A, B - A).y);
//D-A与B-A叉积结果大等于0时返回1 小于0时返回-1
float sign4 = Mathf.Sign(Vector3.Cross(D - A, B - A).y);
//AB与CD相交返回true 否则返回false
return !Mathf.Approximately(sign1, sign2) && !Mathf.Approximately(sign3, sign4);
}
private void OnDrawGizmos()
{
if (a == null || b == null || c == null || d == null) return;
Handles.Label(a.position, "A");
Handles.Label(b.position, "B");
Handles.Label(c.position, "C");
Handles.Label(d.position, "D");
bool flag = IsIntersection(a.position, b.position, c.position, d.position);
Handles.color = flag ? Color.cyan : Color.red;
Handles.DrawLine(a.position, b.position);
Handles.DrawLine(c.position, d.position);
}
}2.如何判断一个点是否在一个凸边形范围内(2D、xz轴构成的平面):
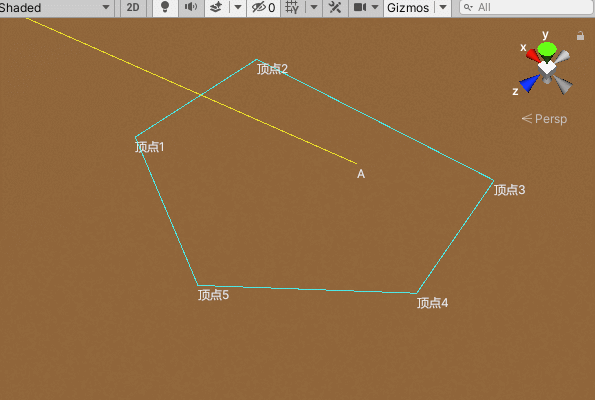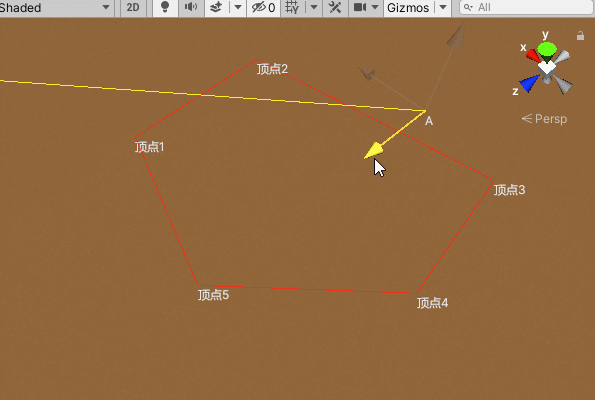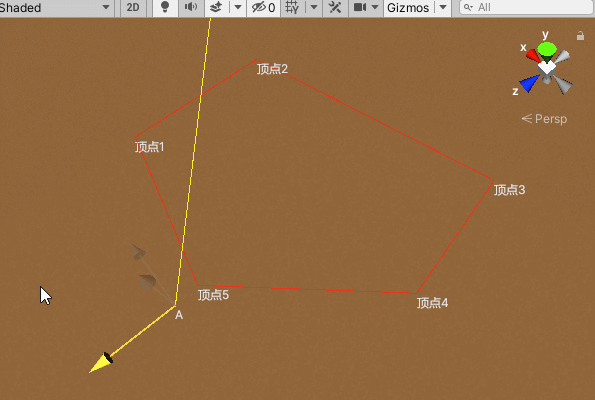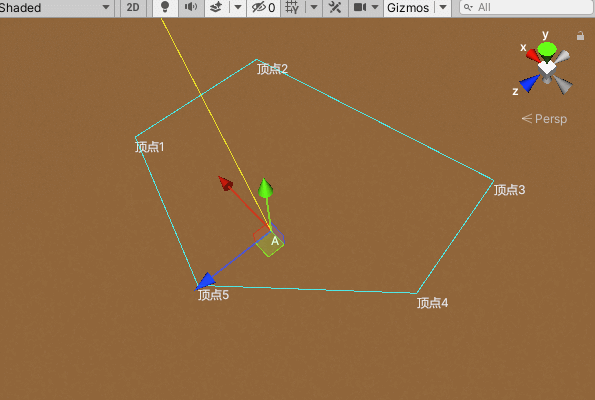
若从该点发出的射线与平面内凸边形的交点的个数为偶数,则点在凸边形外,若为奇数,则点在凸边形内。因此取一条从该点向凸边形发出的射线,遍历凸边形的每一条边,判断射线与边的交点个数,若个数为奇数,则可以判断该点在凸边形范围内。
//判断点A是否在凸边型范围内
private bool IsInRange(Transform[] points, Vector3 A)
{
//取第一条边中点
Vector3 half01 = (points[0].position + points[1].position) * .5f;
//中点延伸(射线)
half01 += (half01 - A).normalized * 100000;
//用于记录交点的个数
int count = 0;
//遍历
for (int i = 0; i < points.Length; i++)
{
var a = points[i % points.Length];
var b = points[(i + 1) % points.Length];
//判断是否相交
if (IsIntersection(a.position, b.position, A, half01)) count++;
}
//交点个数为奇数则表示点A在凸边型范围内
return count % 2 == 1;
}
测试代码如下:
using UnityEngine;
using UnityEditor;
public class Example : MonoBehaviour
{
[SerializeField] private Transform point;
[SerializeField] private Transform[] points; //凸边型顶点集合
//判断点A是否在凸边型范围内
private bool IsInRange(Transform[] points, Vector3 A)
{
//取第一条边中点
Vector3 half01 = (points[0].position + points[1].position) * .5f;
//中点延伸(射线)
half01 += (half01 - A).normalized * 100000;
//用于记录交点的个数
int count = 0;
//遍历
for (int i = 0; i < points.Length; i++)
{
var a = points[i % points.Length];
var b = points[(i + 1) % points.Length];
//判断是否相交
if (IsIntersection(a.position, b.position, A, half01)) count++;
}
//交点个数为奇数则表示点A在凸边型范围内
return count % 2 == 1;
}
//判断AB与CD是否相交
private bool IsIntersection(Vector3 A, Vector3 B, Vector3 C, Vector3 D)
{
//A-D与C-D叉积结果大等于0时返回1 小于0时返回-1
float sign1 = Mathf.Sign(Vector3.Cross(A - D, C - D).y);
//B-D与C-D叉积结果大等于0时返回1 小于0时返回-1
float sign2 = Mathf.Sign(Vector3.Cross(B - D, C - D).y);
//C-A与B-A叉积结果大等于0时返回1 小于0时返回-1
float sign3 = Mathf.Sign(Vector3.Cross(C - A, B - A).y);
//D-A与B-A叉积结果大等于0时返回1 小于0时返回-1
float sign4 = Mathf.Sign(Vector3.Cross(D - A, B - A).y);
//AB与CD相交返回true 否则返回false
return !Mathf.Approximately(sign1, sign2) && !Mathf.Approximately(sign3, sign4);
}
private void OnDrawGizmos()
{
if (points.Length < 3 || point == null) return;
bool flag = IsInRange(points, point.position);
Handles.Label(point.position, "A");
Vector3 half01 = (points[0].position + points[1].position) * .5f;
half01 += (half01 - point.position).normalized * 100000;
for (int i = 0; i < points.Length; i++)
{
var a = points[i % points.Length];
var b = points[(i + 1) % points.Length];
Handles.color = flag ? Color.cyan : Color.red;
Handles.DrawLine(a.position, b.position);
Handles.Label(points[i].position, $"顶点{i + 1}");
Handles.color = Color.yellow;
if (IsIntersection(a.position, b.position, point.position, half01))
{
Handles.DrawLine(point.position, half01);
}
}
}
}3.如何判断一个点是否在一个凸边体范围内(3D):
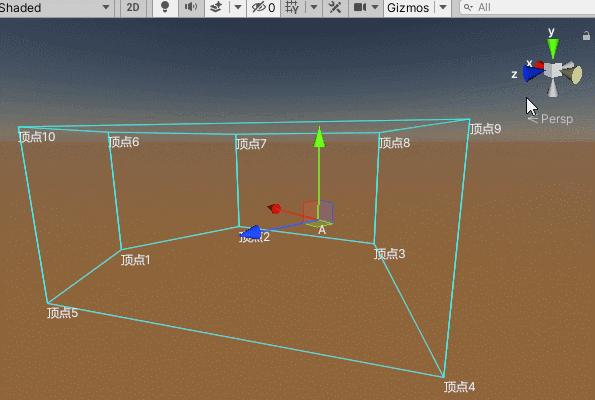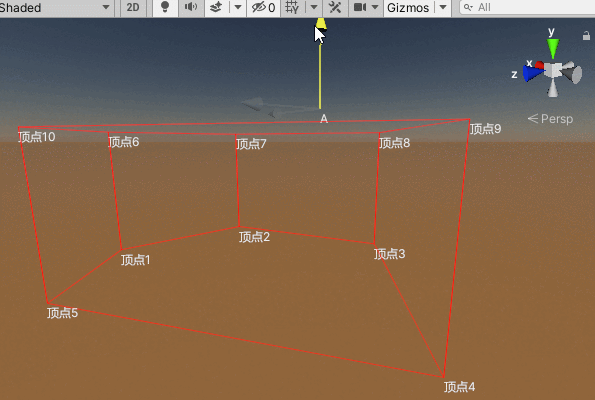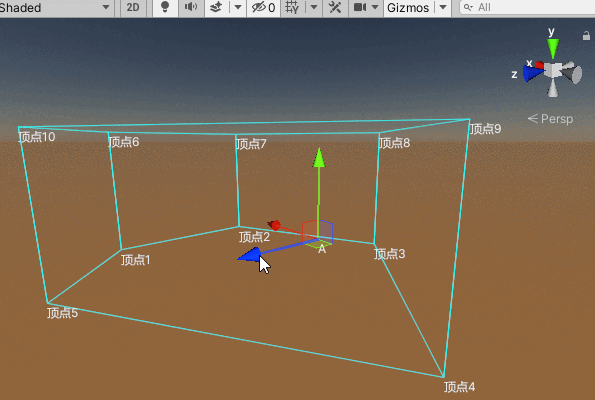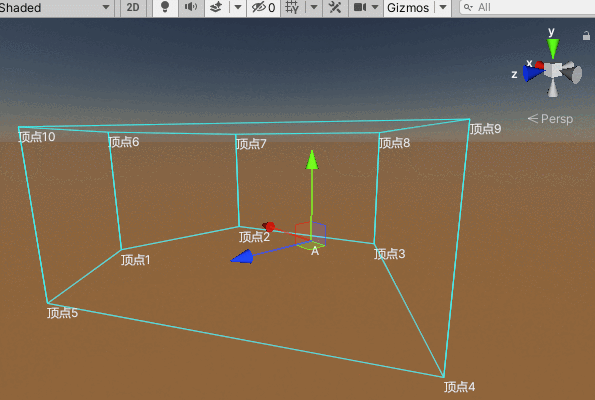
上述部分我们在xz轴所在的平面构建了一个凸边形,现在我们给其一个高度,即可构成一个凸边体空间区域:
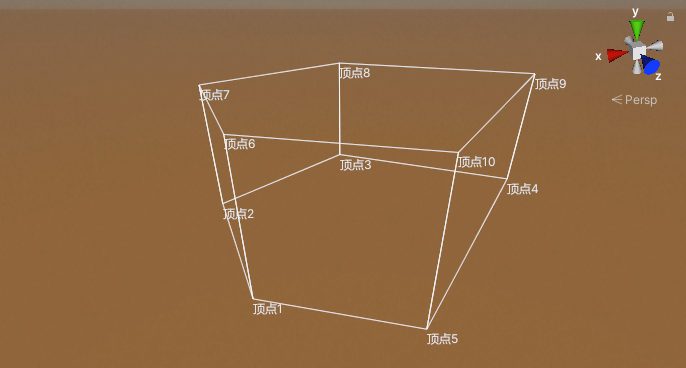
要判断一个点是否在该凸边体范围内,只需要在满足处于xz轴所在的凸边形范围内的同时,其坐标点的y值既小等于凸边体height高度值的一半,又大等于负的高度值的一半:
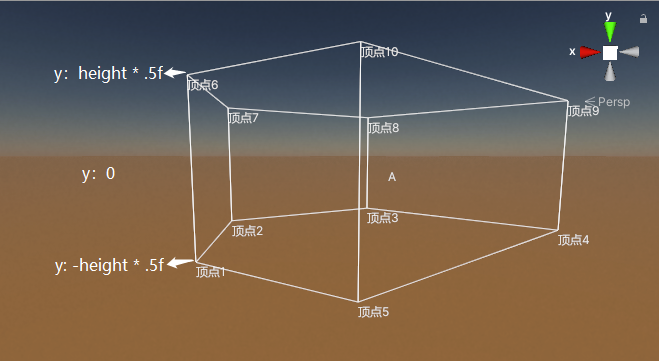
封装判断函数:
//判断点A是否在凸边体范围内
private bool IsInRange(Transform[] points, float height, Vector3 A)
{
bool flag = true;
flag &= A.y <= height * .5f;
flag &= A.y >= -height * .5f;
flag &= IsInRange(points, A);
return flag;
} 
测试代码如下:
using UnityEngine;
using UnityEditor;
public class Example : MonoBehaviour
{
[SerializeField] private Transform point;
[SerializeField] private Transform[] points; //凸边型顶点集合
[SerializeField] private float height = 1f;
//判断点A是否在凸边体范围内
private bool IsInRange(Transform[] points, float height, Vector3 A)
{
bool flag = true;
flag &= A.y <= height * .5f;
flag &= A.y >= -height * .5f;
flag &= IsInRange(points, A);
return flag;
}
//判断点A是否在凸边型范围内
private bool IsInRange(Transform[] points, Vector3 A)
{
//取第一条边中点
Vector3 half01 = (points[0].position + points[1].position) * .5f;
//中点延伸(射线)
half01 += (half01 - A).normalized * 100000;
//用于记录交点的个数
int count = 0;
//遍历
for (int i = 0; i < points.Length; i++)
{
var a = points[i % points.Length];
var b = points[(i + 1) % points.Length];
//判断是否相交
if (IsIntersection(a.position, b.position, A, half01)) count++;
}
//交点个数为奇数则表示点A在凸边型范围内
return count % 2 == 1;
}
//判断AB与CD是否相交
private bool IsIntersection(Vector3 A, Vector3 B, Vector3 C, Vector3 D)
{
//A-D与C-D叉积结果大等于0时返回1 小于0时返回-1
float sign1 = Mathf.Sign(Vector3.Cross(A - D, C - D).y);
//B-D与C-D叉积结果大等于0时返回1 小于0时返回-1
float sign2 = Mathf.Sign(Vector3.Cross(B - D, C - D).y);
//C-A与B-A叉积结果大等于0时返回1 小于0时返回-1
float sign3 = Mathf.Sign(Vector3.Cross(C - A, B - A).y);
//D-A与B-A叉积结果大等于0时返回1 小于0时返回-1
float sign4 = Mathf.Sign(Vector3.Cross(D - A, B - A).y);
//AB与CD相交返回true 否则返回false
return !Mathf.Approximately(sign1, sign2) && !Mathf.Approximately(sign3, sign4);
}
private void OnDrawGizmos()
{
if (points.Length < 3 || point == null) return;
bool flag = IsInRange(points, height, point.position);
Handles.color = flag ? Color.cyan : Color.red;
Handles.Label(point.position, "A");
for (int i = 0; i < points.Length; i++)
{
Handles.Label(points[i].position - new Vector3(0, height * .5f, 0), $"顶点{i + 1}");
Handles.Label(points[i].position + new Vector3(0, height * .5f, 0), $"顶点{i + 1 + points.Length}");
var a = points[i % points.Length];
var b = points[(i + 1) % points.Length];
var minA = a.position - new Vector3(0, height * .5f, 0);
var maxA = a.position + new Vector3(0, height * .5f, 0);
var minB = b.position - new Vector3(0, height * .5f, 0);
var maxB = b.position + new Vector3(0, height * .5f, 0);
Handles.DrawAAPolyLine(minA, minB);
Handles.DrawAAPolyLine(maxA, maxB);
Handles.DrawAAPolyLine(minA, maxA);
Handles.DrawAAPolyLine(minB, maxB);
}
}
}
4.如何判断一个物体是否在一个凸边体范围内:
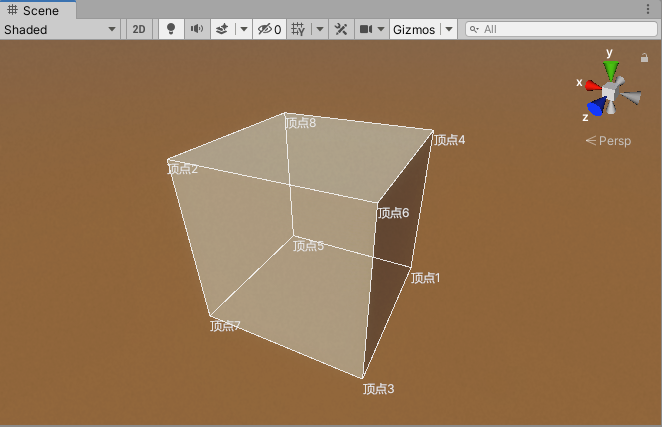
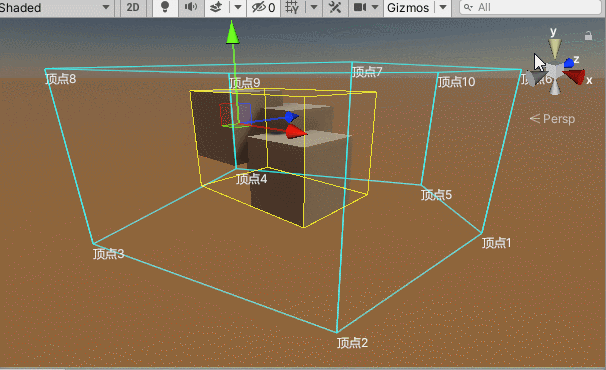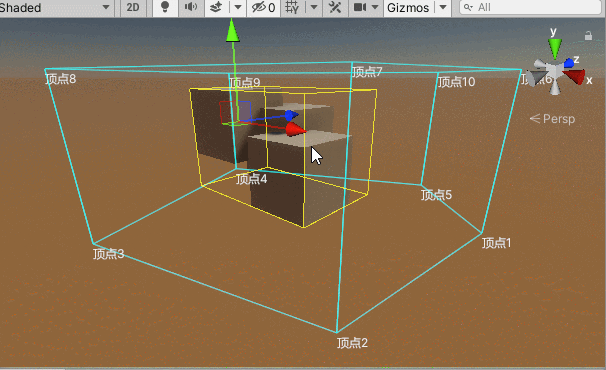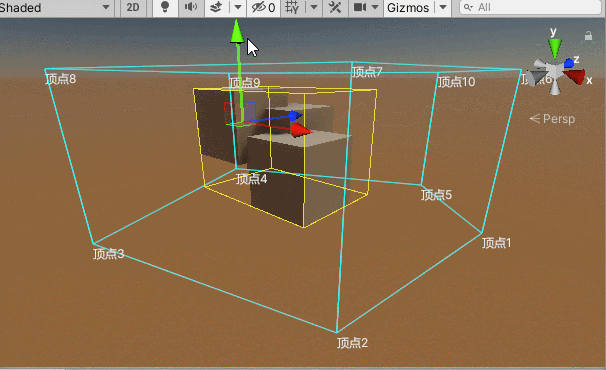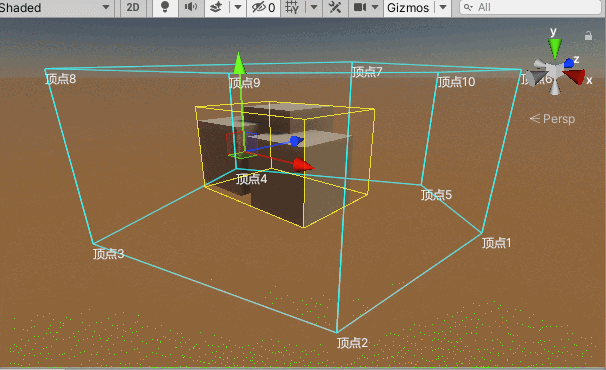
上述部分判断的是一个坐标点是否在一个凸边体范围内,要判断一个物体是否被该凸边体区域所囊括,需要获取该物体及其子物体构成的Bounds边界盒,如果Bounds边界盒的每一个顶点都在该凸边体范围内,则可以大致推断该物体被这个凸边体所囊括,当然要想更精确还是要获取该物体的更为精确的边界点,在这里不做延申。
首先来看Unity圣典中关于Bounds边界盒及其核心变量的介绍:

其中max、min分别是最大、最小点,可以通过这两点获取到其它各顶点的坐标,测试代码如下:
using UnityEngine;
using UnityEditor;
public class Example : MonoBehaviour
{
[SerializeField] private GameObject obj;
private void OnDrawGizmos()
{
if (obj == null) return;
Bounds bounds = obj.GetComponent<MeshRenderer>().bounds;
Vector3 point1 = bounds.min;
Vector3 point2 = bounds.max;
Vector3 point3 = new Vector3(point1.x, point1.y, point2.z);
Vector3 point4 = new Vector3(point1.x, point2.y, point1.z);
Vector3 point5 = new Vector3(point2.x, point1.y, point1.z);
Vector3 point6 = new Vector3(point1.x, point2.y, point2.z);
Vector3 point7 = new Vector3(point2.x, point1.y, point2.z);
Vector3 point8 = new Vector3(point2.x, point2.y, point1.z);
Handles.DrawLine(point6, point2);
Handles.DrawLine(point2, point8);
Handles.DrawLine(point8, point4);
Handles.DrawLine(point4, point6);
Handles.DrawLine(point3, point7);
Handles.DrawLine(point7, point5);
Handles.DrawLine(point5, point1);
Handles.DrawLine(point1, point3);
Handles.DrawLine(point6, point3);
Handles.DrawLine(point2, point7);
Handles.DrawLine(point8, point5);
Handles.DrawLine(point4, point1);
Handles.Label(point1, "顶点1");
Handles.Label(point2, "顶点2");
Handles.Label(point3, "顶点3");
Handles.Label(point4, "顶点4");
Handles.Label(point5, "顶点5");
Handles.Label(point6, "顶点6");
Handles.Label(point7, "顶点7");
Handles.Label(point8, "顶点8");
}
}
一个物体可能包含若干个带有MeshRenderer组件的子物体,因此我们要获取一个囊括所有的Bounds边界盒,要使用到Bounds类中的Encapsulate函数:
using UnityEngine;
using UnityEditor;
public class Example : MonoBehaviour
{
[SerializeField] private GameObject obj;
private void OnDrawGizmos()
{
if (obj == null) return;
Bounds bounds = new Bounds(Vector3.zero, Vector3.zero);
//获取所有MeshRenderer 包括子物体
var mrs = obj.GetComponentsInChildren<MeshRenderer>(true);
Vector3 center = Vector3.zero;
for (int i = 0; i < mrs.Length; i++)
{
center += mrs[i].bounds.center;
//Encapsulate函数重新计算bounds
bounds.Encapsulate(mrs[i].bounds);
}
Vector3 point1 = bounds.min;
Vector3 point2 = bounds.max;
Vector3 point3 = new Vector3(point1.x, point1.y, point2.z);
Vector3 point4 = new Vector3(point1.x, point2.y, point1.z);
Vector3 point5 = new Vector3(point2.x, point1.y, point1.z);
Vector3 point6 = new Vector3(point1.x, point2.y, point2.z);
Vector3 point7 = new Vector3(point2.x, point1.y, point2.z);
Vector3 point8 = new Vector3(point2.x, point2.y, point1.z);
Handles.DrawLine(point6, point2);
Handles.DrawLine(point2, point8);
Handles.DrawLine(point8, point4);
Handles.DrawLine(point4, point6);
Handles.DrawLine(point3, point7);
Handles.DrawLine(point7, point5);
Handles.DrawLine(point5, point1);
Handles.DrawLine(point1, point3);
Handles.DrawLine(point6, point3);
Handles.DrawLine(point2, point7);
Handles.DrawLine(point8, point5);
Handles.DrawLine(point4, point1);
Handles.Label(point1, "顶点1");
Handles.Label(point2, "顶点2");
Handles.Label(point3, "顶点3");
Handles.Label(point4, "顶点4");
Handles.Label(point5, "顶点5");
Handles.Label(point6, "顶点6");
Handles.Label(point7, "顶点7");
Handles.Label(point8, "顶点8");
}
}
封装判断函数:
//判断一个物体是否在凸边体范围内
private bool IsInRange(Transform[] points, float height, GameObject obj)
{
Bounds bounds = new Bounds(Vector3.zero, Vector3.zero);
//获取所有MeshRenderer 包括子物体
var mrs = obj.GetComponentsInChildren<MeshRenderer>(true);
Vector3 center = Vector3.zero;
for (int i = 0; i < mrs.Length; i++)
{
center += mrs[i].bounds.center;
//Encapsulate函数重新计算bounds
bounds.Encapsulate(mrs[i].bounds);
}
Vector3 min = bounds.min;
Vector3 max = bounds.max;
return IsInRange(points, height, min)
&& IsInRange(points, height, max)
&& IsInRange(points, height, new Vector3(min.x, min.y, max.z))
&& IsInRange(points, height, new Vector3(min.x, max.y, min.z))
&& IsInRange(points, height, new Vector3(max.x, min.y, min.z))
&& IsInRange(points, height, new Vector3(min.x, max.y, max.z))
&& IsInRange(points, height, new Vector3(max.x, min.y, max.z))
&& IsInRange(points, height, new Vector3(max.x, max.y, min.z));
}
测试代码如下:
using UnityEngine;
using UnityEditor;
public class Example : MonoBehaviour
{
[SerializeField] private GameObject obj;
[SerializeField] private Transform[] points; //凸边型顶点集合
[SerializeField] private float height = 1f;
//判断一个物体是否在凸边体范围内
private bool IsInRange(Transform[] points, float height, GameObject obj)
{
Bounds bounds = new Bounds(Vector3.zero, Vector3.zero);
//获取所有MeshRenderer 包括子物体
var mrs = obj.GetComponentsInChildren<MeshRenderer>(true);
Vector3 center = Vector3.zero;
for (int i = 0; i < mrs.Length; i++)
{
center += mrs[i].bounds.center;
//Encapsulate函数重新计算bounds
bounds.Encapsulate(mrs[i].bounds);
}
Vector3 min = bounds.min;
Vector3 max = bounds.max;
return IsInRange(points, height, min)
&& IsInRange(points, height, max)
&& IsInRange(points, height, new Vector3(min.x, min.y, max.z))
&& IsInRange(points, height, new Vector3(min.x, max.y, min.z))
&& IsInRange(points, height, new Vector3(max.x, min.y, min.z))
&& IsInRange(points, height, new Vector3(min.x, max.y, max.z))
&& IsInRange(points, height, new Vector3(max.x, min.y, max.z))
&& IsInRange(points, height, new Vector3(max.x, max.y, min.z));
}
//判断点A是否在凸边体范围内
private bool IsInRange(Transform[] points, float height, Vector3 A)
{
bool flag = true;
flag &= A.y <= height * .5f;
flag &= A.y >= -height * .5f;
flag &= IsInRange(points, A);
return flag;
}
//判断点A是否在凸边型范围内
private bool IsInRange(Transform[] points, Vector3 A)
{
//取第一条边中点
Vector3 half01 = (points[0].position + points[1].position) * .5f;
//中点延伸(射线)
half01 += (half01 - A).normalized * 100000;
//用于记录交点的个数
int count = 0;
//遍历
for (int i = 0; i < points.Length; i++)
{
var a = points[i % points.Length];
var b = points[(i + 1) % points.Length];
//判断是否相交
if (IsIntersection(a.position, b.position, A, half01)) count++;
}
//交点个数为奇数则表示点A在凸边型范围内
return count % 2 == 1;
}
//判断AB与CD是否相交
private bool IsIntersection(Vector3 A, Vector3 B, Vector3 C, Vector3 D)
{
//A-D与C-D叉积结果大等于0时返回1 小于0时返回-1
float sign1 = Mathf.Sign(Vector3.Cross(A - D, C - D).y);
//B-D与C-D叉积结果大等于0时返回1 小于0时返回-1
float sign2 = Mathf.Sign(Vector3.Cross(B - D, C - D).y);
//C-A与B-A叉积结果大等于0时返回1 小于0时返回-1
float sign3 = Mathf.Sign(Vector3.Cross(C - A, B - A).y);
//D-A与B-A叉积结果大等于0时返回1 小于0时返回-1
float sign4 = Mathf.Sign(Vector3.Cross(D - A, B - A).y);
//AB与CD相交返回true 否则返回false
return !Mathf.Approximately(sign1, sign2) && !Mathf.Approximately(sign3, sign4);
}
private void OnDrawGizmos()
{
if (points.Length < 3 || obj == null) return;
bool flag = IsInRange(points, height, obj);
Handles.color = flag ? Color.cyan : Color.red;
for (int i = 0; i < points.Length; i++)
{
Handles.Label(points[i].position - new Vector3(0, height * .5f, 0), $"顶点{i + 1}");
Handles.Label(points[i].position + new Vector3(0, height * .5f, 0), $"顶点{i + 1 + points.Length}");
var a = points[i % points.Length];
var b = points[(i + 1) % points.Length];
var minA = a.position - new Vector3(0, height * .5f, 0);
var maxA = a.position + new Vector3(0, height * .5f, 0);
var minB = b.position - new Vector3(0, height * .5f, 0);
var maxB = b.position + new Vector3(0, height * .5f, 0);
Handles.DrawAAPolyLine(minA, minB);
Handles.DrawAAPolyLine(maxA, maxB);
Handles.DrawAAPolyLine(minA, maxA);
Handles.DrawAAPolyLine(minB, maxB);
}
Bounds bounds = new Bounds(Vector3.zero, Vector3.zero);
//获取所有MeshRenderer 包括子物体
var mrs = obj.GetComponentsInChildren<MeshRenderer>(true);
Vector3 center = Vector3.zero;
for (int i = 0; i < mrs.Length; i++)
{
center += mrs[i].bounds.center;
//Encapsulate函数重新计算bounds
bounds.Encapsulate(mrs[i].bounds);
}
Vector3 point1 = bounds.min;
Vector3 point2 = bounds.max;
Vector3 point3 = new Vector3(point1.x, point1.y, point2.z);
Vector3 point4 = new Vector3(point1.x, point2.y, point1.z);
Vector3 point5 = new Vector3(point2.x, point1.y, point1.z);
Vector3 point6 = new Vector3(point1.x, point2.y, point2.z);
Vector3 point7 = new Vector3(point2.x, point1.y, point2.z);
Vector3 point8 = new Vector3(point2.x, point2.y, point1.z);
Handles.color = Color.yellow;
Handles.DrawLine(point6, point2);
Handles.DrawLine(point2, point8);
Handles.DrawLine(point8, point4);
Handles.DrawLine(point4, point6);
Handles.DrawLine(point3, point7);
Handles.DrawLine(point7, point5);
Handles.DrawLine(point5, point1);
Handles.DrawLine(point1, point3);
Handles.DrawLine(point6, point3);
Handles.DrawLine(point2, point7);
Handles.DrawLine(point8, point5);
Handles.DrawLine(point4, point1);
}
}文章来源: coderz.blog.csdn.net,作者:CoderZ1010,版权归原作者所有,如需转载,请联系作者。
原文链接:coderz.blog.csdn.net/article/details/123352634
- 点赞
- 收藏
- 关注作者



评论(0)