算法基础（四）| 前缀和算法及模板详解

⭐写在前面的话：本系列文章旨在复习算法刷题中常用的基础算法与数据结构，配以详细的图例解释，总结相应的代码模板，同时结合例题以达到最佳的学习效果。本专栏面向算法零基础但有一定的C++基础的学习者。若C++基础不牢固，可参考：10min快速回顾C++语法，进行语法复习。

🔥本文已收录于算法基础系列专栏： 算法基础教程 免费订阅，持续更新。

前缀和

一维前缀和

原数组a[i]: a[1], a[2], a[3] … a[n];

前缀和：S[i] = a[1] + a[2] + a[3] …+a[n]

模板1：如何求 $S_i[n]$?

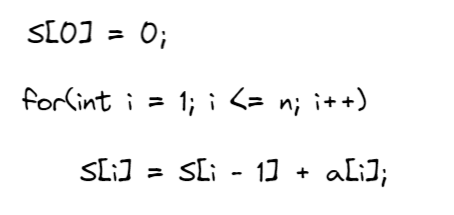
模板2：求[l, r]

$[l, r] = S_r - S_{l-1}$

下标从1开始，为了定义为$S_{0} = 0 $ ,这么定义的好处是可以将 $[l, r] = S_r - S_{l-1}$，这个公式应用在所有场景下，包括 $[1, x] = S[x] - S[0]$ 。

例题：前缀和

输入一个长度为 n 的整数序列。

接下来再输入 m 个询问，每个询问输入一对 l,r。

对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。

输入格式

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式

共 m 行，每行输出一个询问的结果。

数据范围

1≤l≤r≤n,
1≤n,m≤100000
−1000≤数列中元素的值≤1000

输入样例：

5 3
2 1 3 6 4
1 2
1 3
2 4

输出样例：

3
6
10

代码模板

#include<bits/stdc++.h>
using namespace std;

const int N = 100010;

int a[N],s[N];

int main()
{
    ios::sync_with_stdio(false);
    int m , n;
    
    scanf("%d%d", &n ,&m);
    for(int i = 1; i <= n; i++)scanf("%d",&a[i]);
    
    for(int i = 1; i <= n; i++)s[i] = s[i - 1] + a[i];
    
    while( m-- )
    {
        int l ,r;
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l-1]);
    }
    return 0;
}

二维前缀和

S[i][j] : 两个方向的前缀和，左上角这一部分所有元素的和。

a[i][j] : 元素。

首先，写出计算前缀和的公式：

s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]

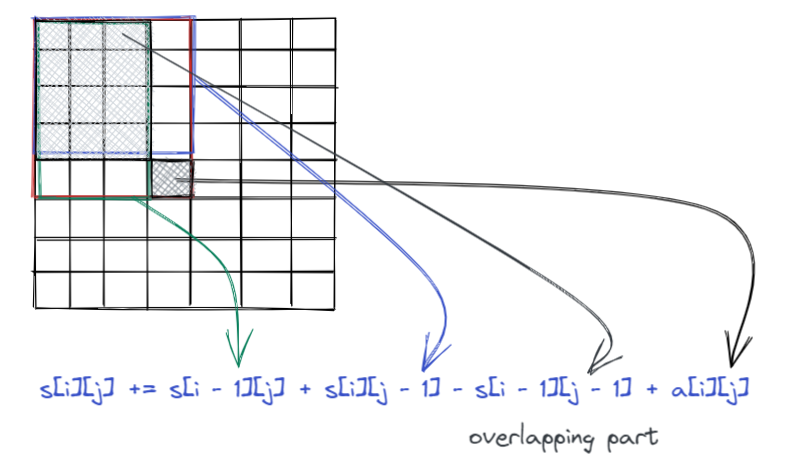
计算部分前缀和的公式如下所示：

s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]

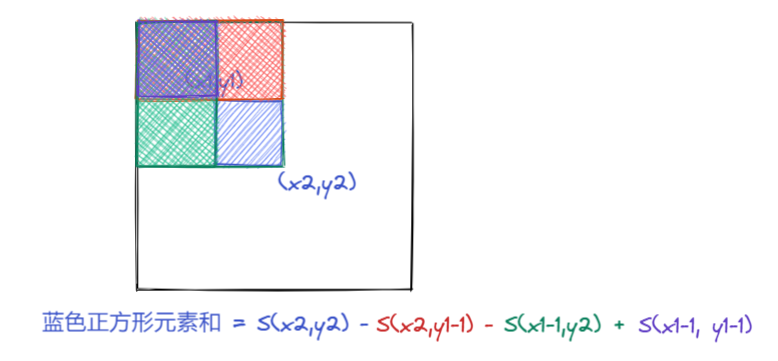
注意，这里把每个格子看成元素就好。

例题：子矩阵的和

输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数 n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式

共 q 行，每行输出一个询问的结果。

数据范围

1≤n,m≤1000
1≤q≤200000
1≤x1≤x2≤n
1≤y1≤y2≤m
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

代码模板

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N],s[N][N];

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        //求前缀和
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];

    while (q -- )
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        //算部分前缀和
        printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }

    return 0;
}