算法基础(三)| 二分图解及代码模板
⭐写在前面的话:本系列文章旨在复习算法刷题中常用的基础算法与数据结构,配以详细的图例解释,总结相应的代码模板,同时结合例题以达到最佳的学习效果。本专栏面向算法零基础但有一定的C++基础的学习者。若C++基础不牢固,可参考:10min快速回顾C++语法,进行语法复习。
🔥本文已收录于算法基础系列专栏: 算法基础教程 免费订阅,持续更新。

二分
整数二分
如果有单调性,就一定可以二分。但是有二分的不一定非得有单调性。
二分的本质是边界,将区间分为两个,一边满足某条性质,另一边不满足某条性质。然后可以找到这两个区间的边界,找任意一个区间的边界都可以。
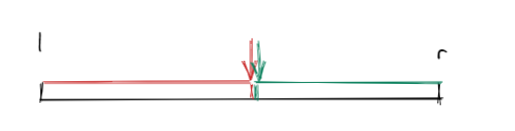
但是找红色边界和绿色边界略有区别:
红色边界:

细节:关于为什么mid = (l + r +1) / 2 ,因为C++中取整是下取整。
- 假设mid = (l + r ) / 2 ;如果是 l = r - 1;那么下取整后 mid = l ,会陷入死循环。
也可以找绿色边界:

例题:数的范围
给定一个按照升序排列的长度为 n 的整数数组,以及 q 个查询。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 00 开始计数)。
如果数组中不存在该元素,则返回 -1 -1。
输入格式
第一行包含整数 n 和 q,表示数组长度和询问个数。
第二行包含 n 个整数(均在 1∼10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 qq 行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回 -1 -1。
数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例:
6 3
1 2 2 3 3 4
3
4
5
输出样例:
3 4
5 5
-1 -1
代码模板
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int m ,n ;
int q[N];
int main()
{
scanf("%d%d", &n, &m);
for(int i = 0; i < n ; i++)scanf("%d",&q[i]);
while( m --)
{
int x;
scanf("%d", &x);
int l = 0 , r = n - 1;
while( l < r)
{
int mid = l + r >> 1;
if(q[mid] >= x)r = mid;
else l = mid + 1;
}
//上面二分出来的是第一个满足大于等于x的数,如果没有x,则是大于x的数。
if(q[l] != x)cout << "-1 -1" <<endl;
//对该数进行判断,如果不满足,则返回-1-1。
else
{
//找到最后一个x的位置
cout << l << ' ';
int l = 0, r = n - 1;
while(l < r)
{
int mid = l + r + 1 >> 1;
if(q[mid] <= x)l = mid;
else r = mid - 1;
}
cout << l << endl;
}
}
}
浮点数二分
浮点数二分思路同上,有个好处是不需要处理边界。
例题:开平方
给定一个浮点数 n,求它的三次方根。
输入格式
共一行,包含一个浮点数 n。
输出格式
共一行,包含一个浮点数,表示问题的解。
注意,结果保留 6 位小数。
数据范围
−10000≤n≤10000
输入样例:
4
输出样例:
2.000000
代码模板
#include<bits/stdc++.h>
using namespace std;
int main()
{
double x;
cin >> x;
double l = 0, r =x ;
while(r - l > 1e-8)
{
double mid = (l + r)/2;
if(mid * mid >= x)r = mid;
else l = mid ;
}
printf("%lf", l);
return 0;
}
这里要强调的是精度问题:
while(r - l > 1e-8)
误差过大会导致精度不足。
这里给出一些经验值:误差值一般比保留位数多2
| 保留位数 | 误差值 |
|---|---|
| 4 | 1e-6 |
| 5 | 1e-7 |
| 6 | 1e-8 |
当然可以采用其他写法:
for(int i = 0; i < 100 ; i++);
直接循环100次,相当于把整个区间的长度直接循环
- 点赞
- 收藏
- 关注作者


评论(0)