0. 前言

最近一直在啃SLAM优化方面的相关知识，发现以前对于se3与sim3之间的理解不太深入，这里专门开一篇文章来整理这两者之间的区别。
相似变换sim(3)，尺度s与R相乘，而不是t。ORB-SLAM2中使用sim3的主要原因是考虑到单目尺度漂移，这个在第一版系统的论文中的VII。 LOOP CLOSING的Compute the Simlilarity Transformation部分有提到。
只有在单目输入的时候，闭环的部分才回使用sim3；其实在双目和RGBD输入的时候虽然也用到了但是其尺度因子被强制设置为1了。

1. 单目尺度漂移

单目SLAM的尺度漂移，简单来说就是单目获得的单张图片无法知道拍摄物体到相机的距离，必须通过对极几何求的两张图片的位姿，然后三角化出来尺度信息。而这些都依赖的是两帧图像之间的逆深度求解。

1. 任选两张图（设为第0帧和第1帧），先提取关键点并匹配，再根据对极几何求本质矩阵E，再从E中恢复R,t。这个在单目VO里属于初始化的部分，其中得到的t是个单位向量，因为任意缩放t，极线约束都成立。你可以对t进行任意缩放。缩放完后，设第0帧的位置为相机坐标系原点，则第1帧的位置就可以由R, t得到。虽然这个t不是真值，但是可以固定下来。然后根据两帧的位置，可以对图像帧0和1中匹配的三维点进行三角化。（多点获取本质矩阵；恢复R,t；并根据R,t三角化计算出伪深度； ）。
   

2. 对之后的图像帧，就不再是利用对极几何求R,t了。依旧是先提取关键点再匹配哈， 但是这次匹配的上一帧的特征中，有些是已经被三角化过的，因此可以像之前答主说的用运动模型加BA求该图像帧与上一帧的位置关系，也可以用PnP求R,t。求出来R,t之后，再三角化该帧与上一帧的没被三角化过的匹配点。
   

我们可以发现在尺度漂移就是出现在第二步。因为对于新的图像帧，都是先计算其R,t，再利用该R,t三角化与之前图像帧匹配的点。问题就是，如果第一步算的R,t有误差，那么第二步三角化的三维点的深度就存在误差，也就是说其深度会存在一个缩放。对于新来的每一帧，都会有这样的问题。

2. SE3与SIM3对比

首先是欧式变换：

然后是相似变换（推导过程同上，故省略）：

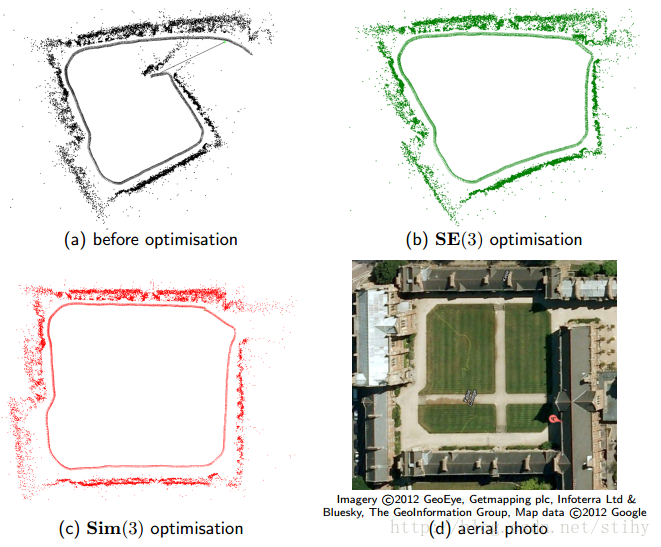
最后说两句，相似变换其实就只是个简单的数学变换而已，所以想思考为什么的时候，应该从数学上来思考才能获得更严谨的论证。相似变换的特点是改变原本物体的尺度比例(保形状)，所以这个S就是要乘在R上，如果在t上，那只是对改变物体的平移量，并不改变形状的尺度比例，上面两个图已经说得很清楚了。这样我们可以发现通过逆深度的缩放将会被考虑在内。

…详情请参照古月居