SLAM本质剖析-G2O

0. 前言

在了解SLAM的原理、流程后，个人经常实时困惑该如何去从零开始去设计编写一套能够符合我们需求的SLAM框架。作者认为Ceres、Eigen、Sophus、G2O这几个函数库无法避免，尤其是Ceres函数库在激光SLAM和V-SLAM的优化中均有着大量的应用。作者分别从Ceres和Eigen两个函数进行了深入的解析，这一篇文章主要对G2O函数库进行详细的阐述，来方便各位后续的开发。

1.G2O示例

相较于Ceres而言，G2O函数库相对较为复杂，但是适用面更加广，可以解决较为复杂的重定位问题。Ceres库向通用的最小二乘问题的求解，定义优化问题，设置一些选项，可通过Ceres求解。而图优化，是把优化问题表现成图的一种方式，这里的图是图论意义上的图。一个图由若干个顶点,以及连着这些顶点的边组成。在这里，我们用顶点表示优化变量，而用边表示误差项。

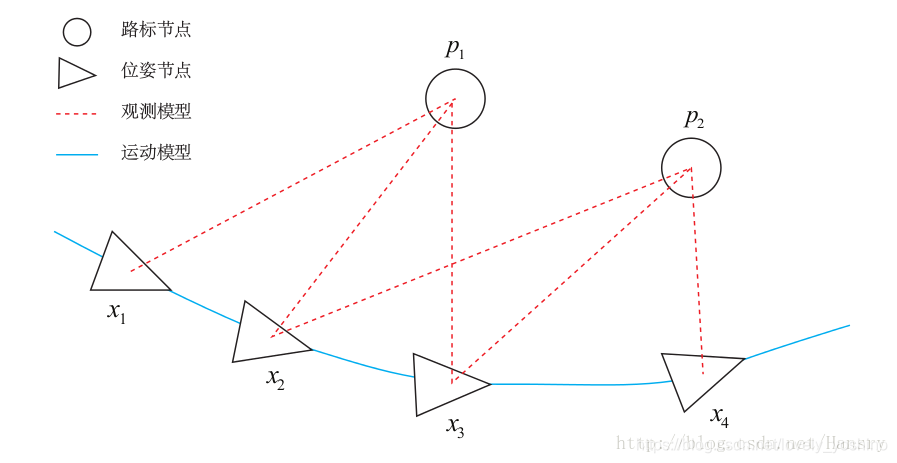
为了使用g2o,首先要将曲线拟合问题抽象成图优化。这个过程中，只要记住节点为优化变量，边为误差项即可。曲线拟合的图优化问题可以画成以下形式：

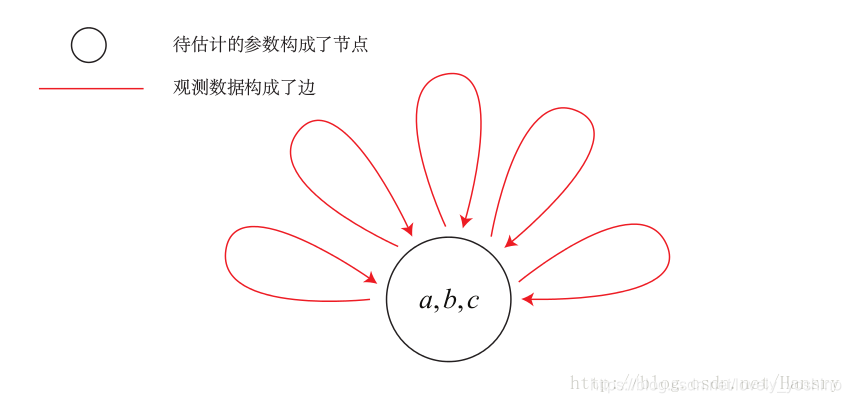
G2O在数学上主要分为四个求解步骤：

在程序中的反应为：

1. 创建一个线性求解器LinearSolver。
2. 创建BlockSolver，并用上面定义的线性求解器初始化。
3. 创建总求解器solver，并从GN/LM/DogLeg 中选一个作为迭代策略，再用上述块求解器BlockSolver初始化。
4. 创建图优化的核心：稀疏优化器（SparseOptimizer）。
5. 定义图的顶点和边，并添加到SparseOptimizer中。
6. 设置优化参数，开始执行优化。

#include <iostream>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/core/optimization_algorithm_dogleg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <Eigen/Core>
#include <opencv2/core/core.hpp>
#include <cmath>
#include <chrono>
using namespace std; 

// 曲线模型的顶点，模板参数：优化变量维度和数据类型(此处为自定义定点，具体可以参考下方的点定义)
class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW// 字节对齐
    virtual void setToOriginImpl() // 重置，设定被优化变量的原始值 
    {
        _estimate << 0,0,0;
    }
    
    virtual void oplusImpl( const double* update ) // 更新
    {
        _estimate += Eigen::Vector3d(update);//update强制类型转换为Vector3d
    }
    // 存盘和读盘：留空
    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}
};

// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
    // 计算曲线模型误差
    void computeError()
    {
        const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);
        const Eigen::Vector3d abc = v->estimate();
        _error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
    }
    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}
public:
    double _x;  // x 值， y 值为 _measurement
};

int main( int argc, char** argv )
{
    double a=1.0, b=2.0, c=1.0;         // 真实参数值
    int N=100;                          // 数据点
    double w_sigma=1.0;                 // 噪声Sigma值
    cv::RNG rng;                        // OpenCV随机数产生器
    double abc[3] = {0,0,0};            // abc参数的估计值

    vector<double> x_data, y_data;      // 数据
    
    cout<<"generating data: "<<endl;
    for ( int i=0; i<N; i++ )
    {
        double x = i/100.0;
        x_data.push_back ( x );
        y_data.push_back (
            exp ( a*x*x + b*x + c ) + rng.gaussian ( w_sigma )
        );
        cout<<x_data[i]<<" "<<y_data[i]<<endl;
    }
    
    // 构建图优化，先设定g2o
    typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block;  // 每个误差项优化变量维度为3，误差值维度为1
    Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 线性方程求解器。第一步：创建一个线性求解器LinearSolver。
    Block* solver_ptr = new Block( linearSolver );      // 矩阵块求解器。第二步：创建BlockSolver，并用上面定义的线性求解器初始化。
    // 梯度下降方法，从GN, LM, DogLeg 中选
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );//第三步：创建BlockSolver，并用上面定义的线性求解器初始化。
    // g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
    // g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
    g2o::SparseOptimizer optimizer;     // 图模型。第四步：创建图优化的核心：稀疏优化器（SparseOptimizer）。
    optimizer.setAlgorithm( solver );   // 设置求解器
    optimizer.setVerbose( true );       // 打开调试输出
    
    // 往图中增加顶点。第五步：定义图的顶点和边HyperGraph，并添加到SparseOptimizer中。
    CurveFittingVertex* v = new CurveFittingVertex();
    v->setEstimate( Eigen::Vector3d(0,0,0) );
    v->setId(0);
    optimizer.addVertex( v );
    
    // 往图中增加边
    for ( int i=0; i<N; i++ )
    {
        CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );
        edge->setId(i);
        edge->setVertex( 0, v );                // 设置连接的顶点
        edge->setMeasurement( y_data[i] );      // 观测数值
        edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵：协方差矩阵之逆
        optimizer.addEdge( edge );
    }
    
    // 执行优化。第六步：设置优化参数，开始执行优化。
    cout<<"start optimization"<<endl;
    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    optimizer.initializeOptimization();
    optimizer.optimize(100);
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>( t2-t1 );
    cout<<"solve time cost = "<<time_used.count()<<" seconds. "<<endl;
    
    // 输出优化值
    Eigen::Vector3d abc_estimate = v->estimate();
    cout<<"estimated model: "<<abc_estimate.transpose()<<endl;
    
    return 0;
}

2. G2O常见函数总结

如下图所示，这个图反应了上述的前五个步骤

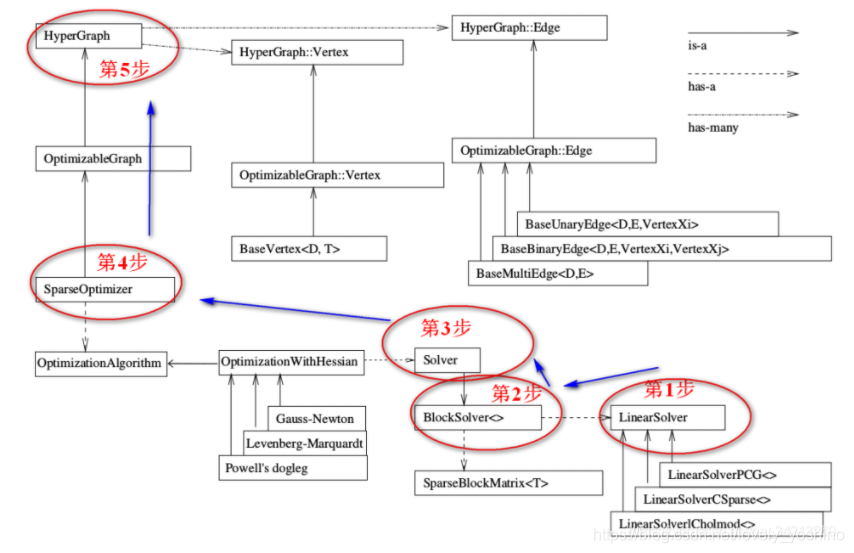
对这个结构框图做一个简单介绍（注意图中三种箭头的含义（右上角注解））：

（1）$\color{#4285f4}{图的核心：整个g2o框架可以分为上下两部分，两部分中间的连接点：SparseOpyimizer 就是整个g2o的核心部分。

（2）往上看，SparseOpyimizer其实是一个Optimizable Graph，从而也是一个超图（HyperGraph）。

（3） $\color{#4285f4}{顶点和边：}$超图有很多顶点和边。顶点继承自 Base Vertex，也即OptimizableGraph::Vertex；而边可以继承自 BaseUnaryEdge（单边）, BaseBinaryEdge（双边）或BaseMultiEdge（多边），它们都叫做OptimizableGraph::Edge。

（4） $\color{#4285f4}{配置SparseOptimizer的优化算法和求解器：}$往下看，SparseOptimizer包含一个优化算法部分OptimizationAlgorithm，它是通过OptimizationWithHessian 来实现的。其中迭代策略可以从**Gauss-Newton（高斯牛顿法，简称GN）、 Levernberg-Marquardt（简称LM法）、Powell’s dogleg **三者中间选择一个（常用的是GN和LM）。

（5） $\color{#4285f4}{如何求解：}$对优化算法部分进行求解的时求解器solver，它实际由BlockSolver 组成。BlockSolver由两部分组成：一个是SparseBlockMatrix，它由于求解稀疏矩阵(雅克比和海塞)；另一个部分是LinearSolver，它用来求解线性方程 得到待求增量，因此这一部分是非常重要的，它可以从PCG/CSparse/Choldmod选择求解方法。

2.1 创建一个线性求解器LinearSolver

我们要求的增量方程的形式是：H△X=-b，通常情况下想到的方法就是直接求逆，也就是△X=-H.inv*b。看起来好像很简单，但这有个前提，就是H的维度较小，此时只需要矩阵的求逆就能解决问题。但是当H的维度较大时，矩阵求逆变得很困难，求解问题也变得很复杂。和Ceres类似，G2O需要一些特殊的方法对矩阵进行求逆。

…详情请参照古月居