算法基础(二)| 高精度算法详解
算法基础(二)| 高精度算法详解
⭐写在前面的话:本系列文章旨在复习算法刷题中常用的基础算法与数据结构,配以详细的图例解释,总结相应的代码模板,同时结合例题以达到最佳的学习效果。本专栏面向算法零基础但有一定的C++基础的学习者。若C++基础不牢固,可参考:10min快速回顾C++语法,进行语法复习。
🔥本文已收录于算法基础系列专栏: 算法基础教程 免费订阅,持续更新。

高精度加法
适用于c++,java和python没有这个问题,因为java有大整数类,python自带,默认数是无限大。
分类:
-
A + B 数量级
-
A - B 数量级
-
A * a 数量级A ≤ ,a ≤ 10000
-
A / a 数量级A ≤ ,a ≤ 10000
大整数的存储
实际上是把长数字的每一位存储到数组当中,并且是倒序存储。
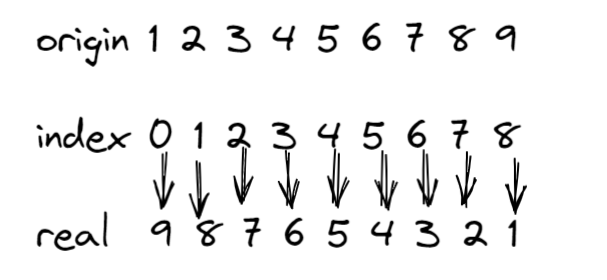
倒序存储的原因:
在数组中,如果顺序存储,在产生进位时,在数组头部a[0]前添加元素非常不方便,需要将后面元素依次后移。而如果倒序存储,则直接可以添加进位数字。
计算过程
先看一下我们如何进行常见加法:
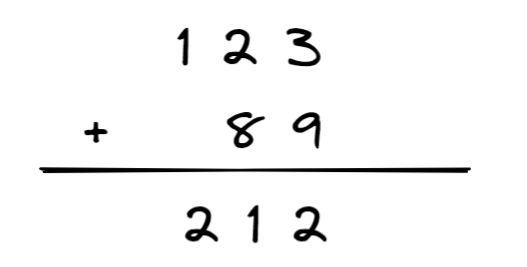
接下来我们将它进行抽象
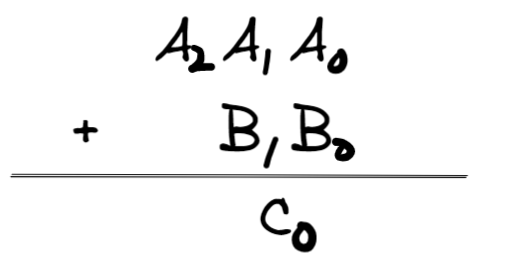
针对其中的一位,我们列以下式子:
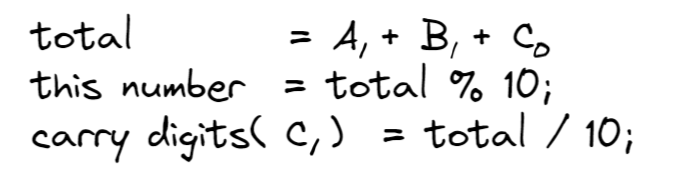
例题:高精度加法
给定两个正整数(不含前导 0),计算它们的和。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的和。
数据范围
1≤整数长度≤100000
12
23
输出样例:
35
算法模板
#include <iostream>
#include <vector>
using namespace std;
//函数是算数组表示的整数A和数组表示的整数B
vector<int> add(vector<int> &A, vector<int> &B)
{
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0;//进位
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
//最后看最高位有没有1,若是1的话就压入
if (t) C.push_back(t);
return C;
}
int main()
{
string a, b;
vector<int> A, B;
cin >> a >> b;
for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
auto C = add(A, B);
for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
cout << endl;
return 0;
}
模板说明
该模板采用了递归调用
vector<int> add(vector<int> &A, vector<int> &B)
{
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0;//进位
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
//最后看最高位有没有1,若是1的话就压入
if (t) C.push_back(t);
return C;
}
此模板也可以换种写法
vector<int> add(vector<int> &A, vector<int> &B)
{
vector<int> C;
int t = 0;//进位
for (int i = 0; i < A.size() || i < B.size(); i ++ )
{
if (i < A.size()) t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
//最后看最高位有没有1,若是1的话就压入
if (t) C.push_back(t);
return C;
}
高精度减法
整数的存储同上
计算过程
这里以下式为例
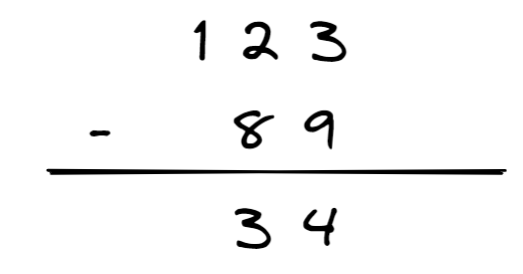
再次把它抽象一下,形成一下形式
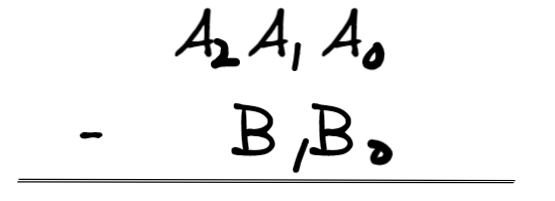
由此我们可以列出以下式子
首先判断A 与 B的关系,如果A 大于B,则正常加减,否则就计算其差的负数。
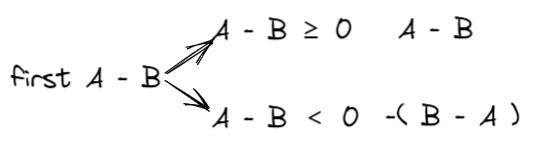
然后分别判断每一位的大小,并且计算是否需要进位。
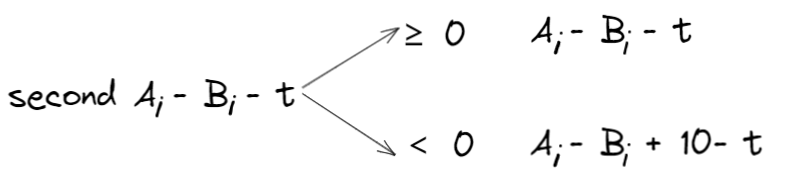
例题:高精度减法
给定两个正整数(不含前导 0),计算它们的差,计算结果可能为负数。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的差。
数据范围
1≤整数长度≤
输入样例:
32
11
输出样例:
21
算法模板
#include <iostream>
#include <vector>
using namespace std;
//判断是否有A ≥ B
bool cmp(vector<int> &A, vector<int> &B)
{
//首先判断两个数的位数大小
if (A.size() != B.size()) return A.size() > B.size();
for (int i = A.size() - 1; i >= 0; i -- )
if (A[i] != B[i])
return A[i] > B[i];
return true;
}
vector<int> sub(vector<int> &A, vector<int> &B)
{
vector<int> C;
for (int i = 0, t = 0; i < A.size(); i ++ )
{
t = A[i] - t;
//首先要判断以下B[i]是否存在
if (i < B.size()) t -= B[i];
//这里的(t + 10) % 10,如果t是0-9,则会抵消,如果t是小于0,则相当于是 +10 借位。
C.push_back((t + 10) % 10);
//t小于0,表示需要借位,因此标记为1
if (t < 0) t = 1;
else t = 0;
}
//删除前导0
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a, b;
vector<int> A, B;
cin >> a >> b;
for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');
vector<int> C;
if (cmp(A, B)) C = sub(A, B);
else C = sub(B, A), cout << '-';
for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
cout << endl;
return 0;
}
高精度乘法
存储与上相同。
计算过程
这里先列出计算式的通式
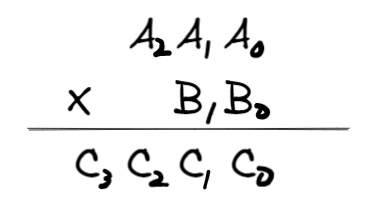
与常见的计算相似,每一位分别考虑进位和取余当前的数字
当前位:
进位:
注意:这里是把B看成一个整体,而不是和一般的乘法一样。这样b方便计算,同时也方便存储(直接存为int就行)。
例题:高精度减法
给定两个正整数(不含前导 0),计算它们的差,计算结果可能为负数。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的差。
数据范围
1≤整数长度≤
输入样例:
32
11
输出样例:
21
算法模板
#include <iostream>
#include <vector>
using namespace std;
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
//进位
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b;
C.push_back(t % 10);
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> A;
for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
auto C = mul(A, b);
for (int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);
return 0;
}
高精度除法
计算过程
高精度除法的通式如下:
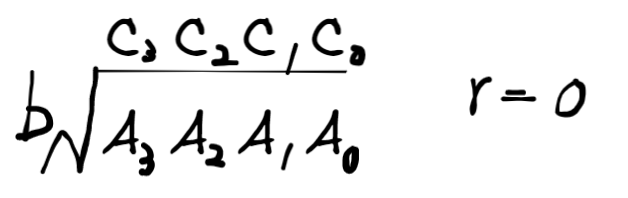
仿照求解除法的过程,可以设计高精度除法算法如下:
最开始余数r为0
-
-
;
-
例题:高精度除法
给定两个非负整数(不含前导 0) A,B,请你计算 A/B 的商和余数。
输入格式
共两行,第一行包含整数 A,第二行包含整数 B。
输出格式
共两行,第一行输出所求的商,第二行输出所求余数。
数据范围
1≤A的长度≤100000
1≤B≤10000
B 一定不为 0
输入样例:
7
2
输出样例:
3
1
算法模板
#include<bits/stdc++.h>
using namespace std;
vector<int> div(vector<int> &A, int b, int &r)
{
vector<int> C;
r = 0;
//这里r为余数
for(int i = A.size() - 1; i >= 0; i--)
{
//余数*10加下一位,输出本位数字为r/b,接着继续取余r
r = r *10 + A[i];
C.push_back(r / b);
r %= b;
}
//由于除法存储是由高到低顺序的,但是通用输出是由低位到高位逆序的,因此这里reverse一下。
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> A;
for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
int r;
auto C = div(A, b,r);
for(int i = C.size() -1 ; i >= 0; i--)printf("%d",C[i]);
cout << endl << r << endl;
return 0;
}
- 点赞
- 收藏
- 关注作者


评论(0)