每日算法刷题Day5-平方矩阵II和III、蛇形矩阵图解
⭐每日算法题解系列文章旨在精选重点与易错的算法题,总结常见的算法思路与可能出现的错误,与笔者另一系列文章有所区别,并不是以知识点的形式提升算法能力,而是以实战习题的形式理解算法,使用算法。

17.平方矩阵 II
输入整数 N,输出一个 N 阶的二维数组。
数组的形式参照样例。
输入格式
输入包含多行,每行包含一个整数 N。
当输入行为 N=0 时,表示输入结束,且该行无需作任何处理。
输出格式
对于每个输入整数 N,输出一个满足要求的 N 阶二维数组。
每个数组占 N 行,每行包含 N 个用空格隔开的整数。
每个数组输出完毕后,输出一个空行。
数据范围
0≤N≤100
输入样例:
1
2
3
4
5
0
输出样例:
1
1 2
2 1
1 2 3
2 1 2
3 2 1
1 2 3 4
2 1 2 3
3 2 1 2
4 3 2 1
1 2 3 4 5
2 1 2 3 4
3 2 1 2 3
4 3 2 1 2
5 4 3 2 1
思路一
通过观察可知,这个矩阵分别是由对角线为1,分别向右和向下延申。
#include<bits/stdc++.h>
using namespace std;
int main(){
const int N= 110;
int n;
int a[N][N];
while(cin>>n,n)
{
for(int i =1;i<=n;i++)
{
for(int j = i,k=1;j<=n;j++,k++)
{//k为赋值数,j为列数
a[i][j]=k;
a[j][i]=k;
}
}
for(int i = 1;i<=n;i++)
{for(int j =1;j<=n;j++)
cout<<a[i][j]<<" ";
cout<<endl;
}
cout<<endl;
}
return 0;
}
思路二
对角线之前的部分是从大到小递减,对角线之后的部分是从小到大递增。
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
while(cin>>n,n){
for(int i = 1;i<=n;i++)
{
//对角线之前的部分,从大到小递减
for(int j = i; j >=1;j--)cout<<j<<" ";
//对角线之后的部分,从小到达递增
for(int j = i+1; j <=n;j++)cout<<j-i+1<<" ";
cout<<endl;
}
cout<<endl;
}
return 0;
}
思路三
找规律。
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
while(cin>>n,n){
for(int i = 1;i<=n;i++)
{
for(int j =1;j<=n;j++)
cout<<abs(i - j)+1<<" ";
cout<<endl;
}
cout<<endl;
}
return 0;
}
18.平方矩阵 III
输入整数 N,输出一个 N 阶的二维数组 M。
这个 N 阶二维数组满足 。
具体形式可参考样例。
输入格式
输入包含多行,每行包含一个整数 N。
当输入行为 N=0 时,表示输入结束,且该行无需作任何处理。
输出格式
对于每个输入整数 N,输出一个满足要求的 N 阶二维数组。
每个数组占 N 行,每行包含 N 个用空格隔开的整数。
每个数组输出完毕后,输出一个空行。
数据范围
0≤N≤15
输入样例:
1
2
3
4
5
0
输出样例:
1
1 2
2 4
1 2 4
2 4 8
4 8 16
1 2 4 8
2 4 8 16
4 8 16 32
8 16 32 64
1 2 4 8 16
2 4 8 16 32
4 8 16 32 64
8 16 32 64 128
16 32 64 128 256
思路
此题找规律即可,每一项都是其横纵坐标分别减一后,对应2的次方得到的。在这里求2的次方采用常用的位移操作。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
while(cin>>n,n)
{
for(int i = 0;i<n;i++)
{
for(int j = 0; j < n ; j++)cout<<(1<<(i+j))<<" ";
cout<<endl;
}
cout<<endl;
}
return 0;
}
19.蛇形矩阵
输入两个整数 n 和 m,输出一个 n 行 m 列的矩阵,将数字 1 到 n×m 按照回字蛇形填充至矩阵中。
具体矩阵形式可参考样例。
输入格式
输入共一行,包含两个整数 n 和 m。
输出格式
输出满足要求的矩阵。
矩阵占 n 行,每行包含 m 个空格隔开的整数。
数据范围
1≤n,m≤100
输入样例:
3 3
输出样例:
1 2 3
8 9 4
7 6 5
思路
介绍一种常见思路:偏移量技巧
关于位移的部分,通常会采用保存一个偏移向量的方式完成。
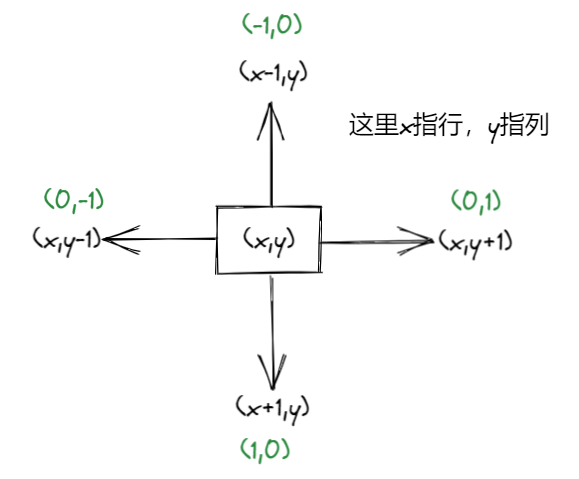
注意:数组最好定义在函数外,因为函数内的数组保存在栈中,栈的限制大小为1MB,可能会造成空间不足的情况。
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int n,m;
int q[N][N];
int main()
{
cin>>n>>m;
int dx[]={-1,0,1,0},dy[]={0,1,0,-1};
int x=0,y=0,d=1;
for(int i = 1;i<=n*m;i++)
{
q[x][y]=i;
int a = x+dx[d],b = y+dy[d];
if(a < 0 || a >= n || b < 0 || b >= m||q[a][b])
//判断条件:越界||已经访问过。
{
d = (d+1)%4;
//切换方向
a = x + dx[d], b = y + dy[d];
}
x = a, y = b;
}
for(int i = 0;i < n; i++)
{
for(int j = 0; j < m; j++)
cout<<q[i][j]<<" ";
cout<<endl;
}
return 0;
}
- 点赞
- 收藏
- 关注作者


评论(0)