前言

上一篇博客构建了线约束和面约束，添加到了残差模块。
ALOAM：后端 lasermapping构建角点约束与面点约束

本片主要介绍通过ceres构建的约束的CostFuction，及后续的通过Ceres进行位姿优化

角点的约束添加在这个地方

这里的CostFunction是通过LidarEdgeFactor自定义的结构体建立的
和前端里程计用的角点约束是一样的在这篇博客中做了分析
原理就是求当前点到a、b点构成的直线的距离作为残差

面点的约束添加在这个地方

输入参数有：

• curr_point 当前点
• norm 归一化得平面法向量
• negative_OA_dot_norm 法向量模的倒数

代码分析

然后可以分析 这个 LidarPlaneNormFactor 自定义的结构体了

struct LidarPlaneNormFactor
{

	LidarPlaneNormFactor(Eigen::Vector3d curr_point_, Eigen::Vector3d plane_unit_norm_,
						 double negative_OA_dot_norm_) : curr_point(curr_point_), plane_unit_norm(plane_unit_norm_),
														 negative_OA_dot_norm(negative_OA_dot_norm_) {}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
 

构造函数，通过生成结构体时的参数，初始化三个变量，和上面的三个是一样的

• curr_point 当前点
• plane_unit_norm 归一化得平面法向量
• negative_OA_dot_norm 法向量模的倒数

	template <typename T>
	bool operator()(const T *q, const T *t, T *residual) const
	{

  

 

  
1
  
2
  
3
 

在前面说了分析Ceres的costfunction重点就是看这个重载（）函数
参数模块在前，残差在后

Eigen::Quaternion<T> q_w_curr{q[3], q[0], q[1], q[2]};

  

 

  
1
 

把q转成 eigen的形式

Eigen::Matrix<T, 3, 1> t_w_curr{t[0], t[1], t[2]};

  

 

  
1
 

把t转成 eigen的形式

Eigen::Matrix<T, 3, 1> cp{T(curr_point.x()), T(curr_point.y()), T(curr_point.z())};

  

 

  
1
 

当前点 转成 eigen 的形式

		Eigen::Matrix<T, 3, 1> point_w;//当前点投影到局部地图坐标系下的点
		point_w = q_w_curr * cp + t_w_curr;//将当前点投影到局部地图坐标系下

  

 

  
1
  
2
 

q_w_curr和t_w_curr是当前帧到局部地图的位姿变换
上面的操作将当前点投影到局部地图上

		Eigen::Matrix<T, 3, 1> norm(T(plane_unit_norm.x()), T(plane_unit_norm.y()), T(plane_unit_norm.z()));
		residual[0] = norm.dot(point_w) + T(negative_OA_dot_norm);//求点到平面的距离

  

 

  
1
  
2
 

第一行就是把法向量转成eigen的形式
第二行就是求点到平面的距离
dot就是点乘，求解和前面说的一样

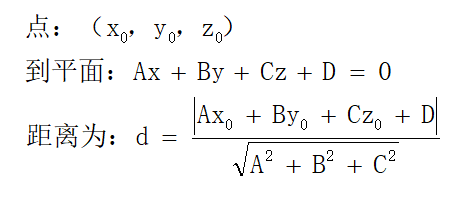
残差可以不取模，因为在ceres里面会平方的。

		return true;
	}

  

 

  
1
  
2
 

最后重载函数返回true即可

	static ceres::CostFunction *Create(const Eigen::Vector3d curr_point_, const Eigen::Vector3d plane_unit_norm_,
									   const double negative_OA_dot_norm_)
	{
		return (new ceres::AutoDiffCostFunction<
				LidarPlaneNormFactor, 1, 4, 3>(
			new LidarPlaneNormFactor(curr_point_, plane_unit_norm_, negative_OA_dot_norm_)));
	}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
 

定义一个Creat函数，在里面实现AutoDiffCostFunction的定义，最后返回一个CostFunction

之后可以回到后端处理cpp—lasermapping.cpp中，在前面的博客添加了角点和面点约束，在上面分析了CostFunction，下面就是调用Ceres求解了

					// 调用Ceres求解
					TicToc t_solver;
					ceres::Solver::Options options;
					options.linear_solver_type = ceres::DENSE_QR;//稠密的问题 用DENSE_QR的求解方式
					options.max_num_iterations = 4;//最大迭代次数
					options.minimizer_progress_to_stdout = false;
					options.check_gradients = false;
					options.gradient_check_relative_precision = 1e-4;
					ceres::Solver::Summary summary;
					ceres::Solve(options, &problem, &summary);//求解
					printf("mapping solver time %f ms \n", t_solver.toc());//一次ceres求解的时间

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

就是Ceres的常规操作了， 由于涉及局部地图了，属于稠密问题，所以求解方式使用的DENSE_QR求解。最大迭代次数为4次。在终端打印一次ceres求解的时间。

Ceres优化时间测试

这优化过程中，在终端设置了这些的打印信息



分别是：

• 构建角点和面点约束的时间
• 一次ceres求解的时间
• 两次迭代优化用的时间

在这篇ALOAM:gazebo仿真测试场景搭建中搭建了测试场景，下面来测试下Ceres的优化时间是多少

场景是这样的，角点和面点很丰富

这个是ALOAM出的地图（AGV没动）

终端打印的数据（一帧）

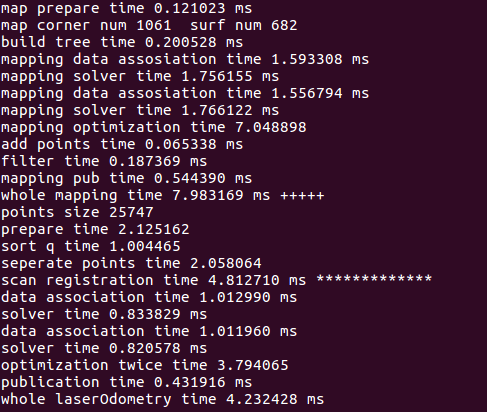
局部地图提取的时间是0.12ms
局部地图中的角点数为1061 面点数是682
建立kd-tree的时间为0.20ms
构建角点和面点约束的时间为 1.59ms
一次ceres求解的时间为 1.75ms
两次迭代优化用的时间 为 7.04ms

文章来源: blog.csdn.net，作者：月照银海似蛟龙，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/qq_32761549/article/details/125914299