前言

通过实物模型产生数字模型的逆向工程应用越来越广泛，SLAM就是其中之一。

该技术在应用中，由于点云的 不完整、旋转错位、平移错位等，使得要得到完整点云就需要对局部点云进行配准。

点云配准定义：为了得到物体的完整数据模型，需要确定一个合适的坐标变换，将从各个视角得到的点集合并到一个统一的坐标系下，形成一个完整的数据点云，这就是点云数据的配准。
其实质就是：把在不同坐标系中测量得到的数据点进行坐标变换，以得到整体的数据模型，问题的关键是如何求得旋转矩阵（R）、平移向量（T），使得两视角下测得的三维数据经坐标变换后的距离最小。

目前，配置算法按照实现过程可以分为 整体配准、局部配准。

一对点云配准

一对点云数据集的配准问题为两两配准（pair registratio）。

通过估计得到的表示平移和旋转的4 × 4刚体变换矩阵来使得一个点云数据集精确的与另一个点云数据集进行完美配置。

具体实现步骤如下：
1、首先从两个数据集中按照同样的关键点选取标准，提取关键点；
2、对选择的所有关键点分别计算其特征描述子；
3、结合特征描述子在两个数据集中的坐标位置，以两者之间特征和位置的相似度为基础，来估算他们的对应关系，初步估计对应点对；
4、假定数据是有噪声的，去除对配准有影响的错误的对应点对；
5、利用剩余的正确的对应关系来估算刚体变换，完成配准。

其中最重要的就是关键点的提取与特征描述，影响准确性和效率的关键两点。

提取关键点和特征描述在其它篇说了，下面说下 对应点对估计

对应点对估计

假设已经得到由两次扫描的点云数据获得的两组特征向量（提取了关键点），在此基础上，必须找到相似特征再确定数据的重叠部分，然后才能进行配准。

根据特征的不同类型，PCL使用不同的方法来搜索特征之间的对应关系。

按照位置来进行对应点估计的，即进行点匹配，（使用点的xyz三维坐标作为特征值），方法有：
1、穷举配准
2、kd-tree 最近邻查询
3、有序点云图像空间查找

按照特征进行匹配时，（不使用点的坐标，而是某些由查询点邻域确定的特征，如法向量、局部或全局形状直方图），有以下几种方法：
1、穷举配准
2、kd-tree 最近邻查询

对应估计也分两种类型：
1、直接对应估计（默认）：点云A中的每一个点搜索点云B中的对应点，确认最终对应点对。
2、互相对应估计：点云A中的点到点云B搜索对应点，然后点云B的点到点云A中搜索对应点，最后只取交集作为对应点对。

PCL中 以函数的形式 让使用者 可以 自由设定和使用。

去除对配准有影响的错误的对应点对

处理外因：
由于噪声的影响，通常并不是所有的估计的对应关系都是正确的。

处理内因：
由于错误的对应关系对于最终的刚体变换矩阵的估算会产生负面影响，所有必须去除他们，

处理方法：
可以使用随机采样一致性估计或者其它方法剔除错位对应关系

处理效果：
最终使用的对应关系数量只使用一定比例的对应关系，这样既可以提高变换矩阵的估计精度，也可以提高配准速度。

变换矩阵估算

估算变换矩阵的步骤如下：
1、在对应关系的基础上，评估一些错误的度量标准
2、在摄像机位姿（运动估算）和最小化错位度量标准下估算一个刚体变换
3、优化点的结构
4、使用刚体变换把源点云旋转/平移到目标点云所在的同一坐标系下，用所有点、点的一个子集或者关键点运行一个内部ICP循环；
5、进行迭代，直到符合收敛性判断标准为止。

迭代最近点算法（ICP）

定义：
ICP算法对待拼接的2片点云，首先根据一定的准则 确立对应点集P与Q ，其中对应点的个数为n。然后通过最小二乘法迭代计算最优的坐标变换，即旋转矩阵R和平移矩阵T，使得误差函数最小。

优点：
ICP算法计算简便直观且可使拼接具有较好的精度。

缺点：
算法的运行速度以及向全局最优的收敛性却在很大程度上依赖与给定的初始变换估计以及迭代过程中对应关系的确立。

ICP处理流程主要分为4个处理步骤：
1、对原始点云数据进行采样
2、确定初始对应点集
3、去除错误对应点对
4、坐标变换求解

采样一致性初始对齐算法 （粗拼接）

该目的主要是给ICP提供一个初始变换

配准算法从精度上分两类，一种是初始的变换矩阵的粗略估计，另一种是像ICP一样的精确的变换矩阵估计。

对于初始的变换矩阵粗略估计，贪婪的初始配准方法工作量大，采用一致性方法的效果会更好。

一致性方法：试图保持相同的对应关系的几何关系。从候选对应关系中进行大量的采样并通过以下的步骤对他们中的每一个进行排名
1、从P中选择s个样本点，同时确定他们的配对距离大于用户设定的最小值
2、对于每个样本点，在Q中找到满足直方图和样本点直方图相似的点存入一个列表中，从这些点中随机选择一些代表采样点的对应关系
3、计算通过采样点定义的刚体变换和其对应变换，计算点云的度量错误来评价转换的质量

使用迭代最近点ICP算法

随机生成一个点云作为源点云，并将其沿X轴平移后作为目标点云，利用ICP估计源到目标的刚体变换矩阵。

Code

～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

#include <iostream>

// PCL 部分
#include <pcl/io/pcd_io.h>
#include <pcl/point_types.h>
#include <pcl/registration/icp.h>   //icp

// Eigen 部分
#include <Eigen/Core>

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
 

头文件部分
用icp 需要 包含 pcl/registration/icp.h
～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_in (new pcl::PointCloud<pcl::PointXYZ>);//声明源点云
    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_out (new pcl::PointCloud<pcl::PointXYZ>);//声明目标点云

  

 

  
1
  
2
 

声明 源点云和目标点云
～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

    /*填充源点云*/
    cloud_in->width    = 5;
    cloud_in->height   = 1;
    cloud_in->is_dense = false;
    cloud_in->points.resize (cloud_in->width * cloud_in->height);
    for (size_t i = 0; i < cloud_in->points.size (); ++i)
    {   
        cloud_in->points[i].x = 1024 * rand () / (RAND_MAX + 1.0f);
        cloud_in->points[i].y = 1024 * rand () / (RAND_MAX + 1.0f);
        cloud_in->points[i].z = 1024 * rand () / (RAND_MAX + 1.0f);
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

填充源点云
～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

    //打印 源点云 点个数
    std::cout << "Saved " << cloud_in->points.size () << " data points to input:"<< std::endl;

    //打印 源点云  的 每个点的坐标
    for (size_t i = 0; i < cloud_in->points.size (); ++i) 
    {
        std::cout << "    " <<
        cloud_in->points[i].x << " " << 
        cloud_in->points[i].y << " " <<
        cloud_in->points[i].z << std::endl;
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

打印 源点云 点个数 源点云 的 每个点的坐标
～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

    //将源点云赋值给目标点云
    *cloud_out = *cloud_in;

    //将目标点云 的 x 坐标 都  平移 0.7
    for (size_t i = 0; i < cloud_in->points.size (); ++i)
    {
        cloud_out->points[i].x = cloud_in->points[i].x + 0.7f;
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

构建目标点云 （源点云x坐标平移0.7）

～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

    //打印 目标点云 点个数     
    std::cout << "Transformed " << cloud_out->points.size () << " data points:"<< std::endl;

    //打印 目标点云  的 每个点的坐标
    for (size_t i = 0; i < cloud_out->points.size (); ++i)
    {
        std::cout << "    " << cloud_out->points[i].x << " " <<
        cloud_out->points[i].y << " " << cloud_out->points[i].z << std::endl;
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
 

打印 目标点云 点个数 目标点云 的 每个点的坐标
～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～
重点

 /* 声明 ICP 对象  */
    pcl::IterativeClosestPoint<pcl::PointXYZ, pcl::PointXYZ> icp;

    /*输入 设置 源点云*/
    icp.setInputCloud(cloud_in);

    /*输入 设置 目标点云*/
    icp.setInputTarget(cloud_out);

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

1、声明 ICP 对象
2、输入 设置 源点云
3、输入 设置 目标点云
～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

    /*有4个参数可以设置 */
    // 设置最大的对应关系距离为 多少 单位m， （对应距离大于此距离将被忽略） 
    icp.setMaxCorrespondenceDistance (0.8);
    // 设置最大迭代次数(默认 1)
    icp.setMaximumIterations (50);
    // 设置 两次变换矩阵之间的差值 (默认 2)
    icp.setTransformationEpsilon (1e-8);
    // 设置 均方误差(默认 3)
    icp.setEuclideanFitnessEpsilon (1);

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
 

有4个参数可以设置
4、设置最大的对应关系距离为 多少 单位m， （对应距离大于此距离将被忽略）
5、设置最大迭代次数
6、设置 两次变换矩阵之间的差值
7、设置 均方误差

此例中 这四个参数可以不设置，使用默认也可以。为后续应用提前总结
～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

    /* 声明 经过配准变换 源点云 后 的 点云 */
    pcl::PointCloud<pcl::PointXYZ> Final;
    /*执行配准  存储变换后的源点云到 Final 上  */
    icp.align(Final); 

    //打印 目标点云 点个数     
    std::cout << "Final " << Final.points.size () << " data points:"<< std::endl;

    //打印 变换后的源点云  的 每个点的坐标    和目标点云是一致的
    for (size_t i = 0; i < Final.points.size (); ++i)
    {
        std::cout << "    " << Final.points[i].x << " " <<
        Final.points[i].y << " " << Final.points[i].z << std::endl;
    }  


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
 

8、 声明 经过配准变换 源点云 后 的 点云 执行配准 存储变换后的源点云到 Final 上
并将点个数与坐标打印

～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

    /* 打印匹配 结果  如果两个点云匹配正确的话 则 icp.hasConverged()为1 */
    std::cout << "has converged:" << icp.hasConverged() << " score: " <<
    icp.getFitnessScore() << std::endl;

  

 

  
1
  
2
  
3
  
4
 

可以通过 icp.hasConverged() 查看匹配结果 如果两个点云匹配正确的话 该函数返回1

～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

    /*声明 最终的变换矩阵*/
    Eigen::Matrix4f transformation;
    //赋值旋转矩阵
    transformation = icp.getFinalTransformation();
    /* 打印输出最终的 变换矩阵 */
    std::cout << icp.getFinalTransformation() << std::endl;

  

 

  
1
  
2
  
3
  
4
  
5
  
6
 

9、通过icp.getFinalTransformation() 函数 返回 最终的变换矩阵

并输出该变换矩阵

～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～
CMakeLists.txt

# 声明要求的 cmake 最低版本
cmake_minimum_required(VERSION 2.8 )
# 声明工程名称
project(iterative_closest_point)
# 添加c++ 11 标准支持
set(CMAKE_CXX_FLAGS "-std=c++11")
#引入Eigen
find_package(Eigen3 REQUIRED)
include_directories(
        ${EIGEN3_INCLUDE_DIR}
	)
#添加头文件  的路径
include_directories(  /usr/local/include/eigen3/ )
# 寻找PCL的库
find_package(PCL REQUIRED COMPONENT common io visualization filters features keypoints)
link_directories(${PCL_LIBRARY_DIRS})
# 添加头文件
include_directories(${PCL_INCLUDE_DIRS})
add_definitions( ${PCL_DEFINITIONS} )
#添加一个可执行程序
add_executable(iterative_closest_point iterative_closest_point.cpp)
#链接PCL 库
target_link_libraries(iterative_closest_point ${PCL_LIBRARIES})

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
 

～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

Result

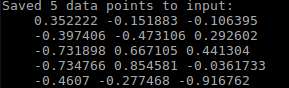
源点云 5个点 及其坐标

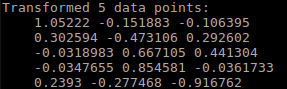
目标点云 5 个点 及其 坐标
可以看到 x 坐标 比源点云的x大0.7

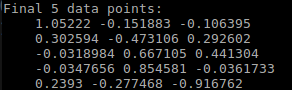
经过 配准变换后 源点云的坐标 ，
可以看到 与 目标点云 相同 。 说明配准完成

配准的结果 与 分数

得到的变换矩阵 最后一列为平移向量 可以看到 约为 （0.7，0，0，1）

如果将这里设置为0.6 ， 那么平移的0.7将 会造成 对应点找不到 出现下面的结果

文章来源: blog.csdn.net，作者：月照银海似蛟龙，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/qq_32761549/article/details/119317559