激光SLAM:代码实现基于非线性最小二乘的图优化
激光SLAM:代码实现基于非线性最小二乘的图优化
在上一篇介绍了如何应用非线性最小二乘来在slam中实现图优化 链接
这篇在其基础上,将代码实现,并进行测试.一定要看懂原理再来看代码
位姿向量转换成变换矩阵
在公式中经常需要把位姿向量转换成变换矩阵,例如:
观测值为匹配计算得到的节点i和节点j的相对位姿:
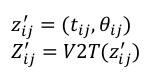
这里的第二行V2T的公式就是把位姿向量转换成变换矩阵.
代码写成函数的形式,方便后面调用.
//位姿向量-->转换矩阵
//函数形参 : 位姿向量 x,y,θ
//函数返回 : 变换矩阵
Eigen::Matrix3d PoseToTrans(Eigen::Vector3d x)
{
Eigen::Matrix3d trans;//声明转换矩阵
trans << cos(x(2)),-sin(x(2)),x(0),
sin(x(2)), cos(x(2)),x(1),
0, 0, 1;
return trans;//返回转换矩阵
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
变换矩阵转换成位姿向量
同样也有把变换矩阵转换成位姿向量的形式,例如:
将观测值和预测值的两个相对位姿计算误差函数的时候
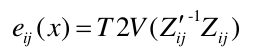
这里的第二行T2V公式就是把变换矩阵转换成位姿向量.
代码写成函数的形式,方便后面调用.
//函数功能 : 转换矩阵-->位姿向量
//函数形参 : 转换矩阵 3*3
//函数返回 : 位姿向量
Eigen::Vector3d TransToPose(Eigen::Matrix3d trans)
{
Eigen::Vector3d pose;//声明位姿向量
pose(0) = trans(0,2);
pose(1) = trans(1,2);
pose(2) = atan2(trans(1,0),trans(0,0));
return pose;//返回位姿向量
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
计算误差向量和Jacobian
下面完成 当点i(xi)与点j(xj)和两个点的观测值(z)[匹配的结果] 后 计算出误差向量(ei)和Jacobian矩阵里的Ai和Bi,有了这三个量就可以计算出b和H矩阵,这个计算在其它函数中进行,首先看ei Ai Bi的计算函数:

红框里的就是要求的三个量,为什么是这个公式,在前面推导了
/**
* 函数名称: CalcJacobianAndError
* 函数功能: 计算jacobian矩阵和error
* @param xi fromIdx
* @param xj toIdx
* @param z 观测值:xj相对于xi的坐标
* @param ei 计算的误差
* @param Ai 相对于xi的Jacobian矩阵
* @param Bi 相对于xj的Jacobian矩阵
*/
void CalcJacobianAndError(Eigen::Vector3d xi,Eigen::Vector3d xj,Eigen::Vector3d z,
Eigen::Vector3d& ei,Eigen::Matrix3d& Ai,Eigen::Matrix3d& Bi)
{
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
函数名称和形参这样设置
由于已知 xi xj z,那么公式里的ti tj θi θj θij 均已知了,那么剩下的就是R的那几个矩阵了
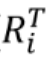
Eigen::Matrix2d RiT;//声明 Ri转置矩阵
RiT << cos(xi(2)),sin(xi(2)),
-sin(xi(2)),cos(xi(2));//赋值
- 1
- 2
- 3
正常的姿态矩阵是:

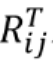
Eigen::Matrix2d RijT;//声明 Rij转置矩阵
RijT << cos(z(2)),sin(z(2)),
-sin(z(2)),cos(z(2));//赋值
- 1
- 2
- 3
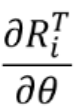
Eigen::Matrix2d dRiT;//声明 Ri 对θ求导的矩阵
dRiT << -sin(xi(2)), cos(xi(2)),
-cos(xi(2)),-sin(xi(2));//赋值
- 1
- 2
- 3
cos的导数是-sin ,sin的导数是cos,所以矩阵就是上面的形式了.
公式里面的所有量都已知了,剩下的就是计算了.
/*ei的计算*/
ei.block(0, 0, 2, 1) = RijT * (RiT * (xj.block(0, 0, 2, 1) - xi.block(0, 0, 2, 1)) - z.block(0, 0, 2, 1));//公式
ei(2) = xj(2) - xi(2) - z(2);//公式
//将角度 限制在 -pi ~ pi
if (ei(2) > M_PI)
ei(2) -= 2 * M_PI;
else if (ei(2) < -M_PI)
ei(2) += 2 * M_PI;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
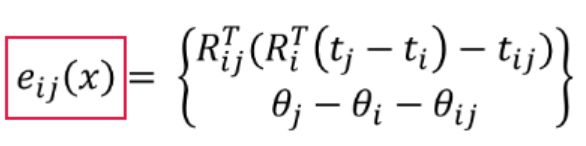
ei的计算,没啥好说的,就是公式带入.最后注意限制角度的范围
/*Ai和Bi的计算*/
Ai.block(0, 0, 2, 2) = - RijT * RiT;//公式
Ai.block(0, 2, 2, 1) = RijT * dRiT * (xj.block(0, 0, 2, 1) - xi.block(0, 0, 2, 1));//公式
Ai.block(2, 0, 1, 3) << 0, 0, -1;//公式
Bi.setIdentity();
Bi.block(0, 0, 2, 2) = RijT * RiT;//公式
- 1
- 2
- 3
- 4
- 5
- 6
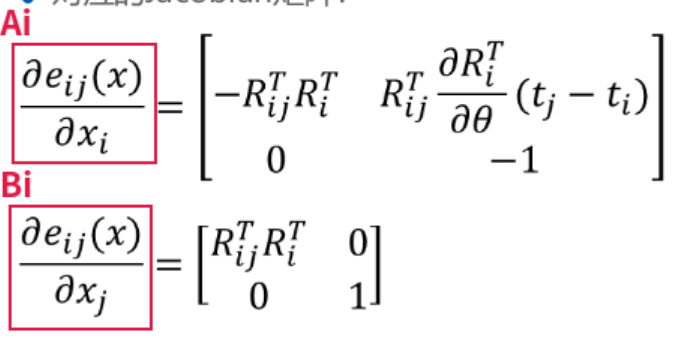
对应公式带入
然后这个函数就完了
一次迭代求解
现在有了一条边的 eij和Ai Bi ,下面需要遍历每条边,生成H和b矩阵,然后就可以求到dx了.一次迭代就完了.下面完成这部分的代码
/**
* @函数名称: LinearizeAndSolve
* @函数功能: 高斯牛顿方法的一次迭代.
* @param Vertexs 图中的所有节点
* @param Edges 图中的所有边
* @return dx 位姿的增量
*/
Eigen::VectorXd LinearizeAndSolve(std::vector<Eigen::Vector3d>& Vertexs,
std::vector<Edge>& Edges)
{
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
函数名称和形参这样设置
//申请内存
Eigen::MatrixXd H(Vertexs.size() * 3,Vertexs.size() * 3);//H矩阵的维度 (点个数*单点纬度) * (点个数*单点纬度)
Eigen::VectorXd b(Vertexs.size() * 3);//b矩阵的维度 (点个数*单点纬度)
H.setZero();//至零
b.setZero();//至零
//固定第一帧
Eigen::Matrix3d I;
I.setIdentity();
H.block(0,0,3,3) += I;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
首先声明H矩阵和b矩阵
H矩阵的维度 (点个数 * 单点纬度) * (点个数 * 单点纬度) 二维的话单点维度就是3 (x,y,θ)
b矩阵的维度 (点个数*单点纬度)
固定第一帧是为了初始化一个固定的位置
//构造H矩阵 & b向量
for(int i = 0; i < Edges.size();i++)
{
//提取信息
Edge tmpEdge = Edges[i];
Eigen::Vector3d xi = Vertexs[tmpEdge.xi];
Eigen::Vector3d xj = Vertexs[tmpEdge.xj];
Eigen::Vector3d z = tmpEdge.measurement;
Eigen::Matrix3d infoMatrix = tmpEdge.infoMatrix;
//计算误差和对应的Jacobian
Eigen::Vector3d ei;
Eigen::Matrix3d Ai;
Eigen::Matrix3d Bi;
CalcJacobianAndError(xi,xj,z,ei,Ai,Bi);
//TODO--Start
b.block(3*tmpEdge.xi, 0, 3, 1) += Ai.transpose() * infoMatrix * ei;
b.block(3*tmpEdge.xj, 0, 3, 1) += Bi.transpose() * infoMatrix * ei;
H.block(3*tmpEdge.xi, 3*tmpEdge.xi, 3, 3) += Ai.transpose() * infoMatrix * Ai;
H.block(3*tmpEdge.xi, 3*tmpEdge.xj, 3, 3) += Ai.transpose() * infoMatrix * Bi;
H.block(3*tmpEdge.xj, 3*tmpEdge.xi, 3, 3) += Bi.transpose() * infoMatrix * Ai;
H.block(3*tmpEdge.xj, 3*tmpEdge.xj, 3, 3) += Bi.transpose() * infoMatrix * Bi;
//TODO--End
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
这部分遍历每个边,去构造H矩阵和b矩阵实际的地方
循环里的第一部分先提取边里的信息,预测值:xi xj 测量值:z 信息矩阵:infoMatrix
然后第二部分用上一环境构造的函数计算ei Ai Bi
第三部分用ei Ai Bi去构造H和b矩阵,添加到相应位置,就按照下面的公式:


//求解
Eigen::VectorXd dx;//声明dx
dx = H.colPivHouseholderQr().solve(-b);//有了H和b即可以求解dx
return dx;//返回dx
}
- 1
- 2
- 3
- 4
- 5
遍历完每条边,那么H和b矩阵就构造完了,即可求出dx并返回该值,完成一次迭代求解.
完成图优化功能
接下来写一个迭代的循环,不断调用一次迭代求解的这个函数,完成图优化功能.
int maxIteration = 100;//最大迭代次数
double epsilon = 1e-4;//精度要求阈值
for(int i = 0; i < maxIteration;i++)//迭代求解
{
std::cout <<"Iterations:"<<i<<std::endl;//输出迭代的次数
Eigen::VectorXd dx = LinearizeAndSolve(Vertexs,Edges);//一次的迭代求解
//进行位姿更新 将上面求解的dx叠加到x上
for(int j = 0; j < Vertexs.size(); ++j)
{
//更新x
Vertexs[j](0) += dx(j*3);
Vertexs[j](1) += dx(j*3+1);
Vertexs[j](2) += dx(j*3+2);
//限制角度
if (Vertexs[j](2) > M_PI)
Vertexs[j](2) -= 2 * M_PI;
else if (Vertexs[j](2) < -M_PI)
Vertexs[j](2) += 2 * M_PI;
}
double maxError = -1;//迭代过程中的dx中的最小值
for(int k = 0; k < 3 * Vertexs.size();k++)
{
if(maxError < std::fabs(dx(k)))
{
maxError = std::fabs(dx(k));
}
}
if(maxError < epsilon)//精度满足要求则跳出优化
break;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
通过一个for循环,不断迭代,不断调用一次迭代求解的这个函数,完成图优化功能.
一个判断精度是否满足要求的判断,精度满足要求或者达到最大的迭代次数后,则作为最终的优化结果.
位姿图显示
在进行优化前,可以调用之前写的rviz显示位姿图的函数,来可视化优化前后的结果
//调用 rivz poes graph 显示功能函数
PublishGraphForVisulization(&beforeGraphPub,
Vertexs,
Edges);
- 1
- 2
- 3
- 4
PublishGraphForVisulization(&afterGraphPub,
Vertexs,
Edges,1);
- 1
- 2
- 3
Result
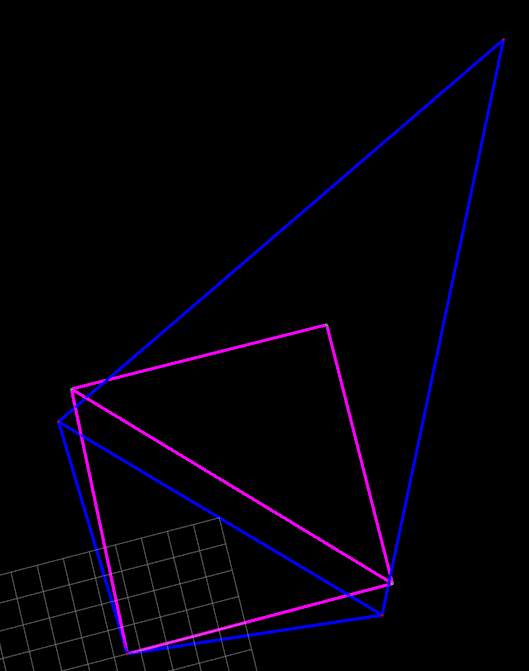
上面是一个测试用的位姿图例子,仅有四个点,五个边
蓝色的是图优化前的位姿图
粉色的是图优化后的位姿图
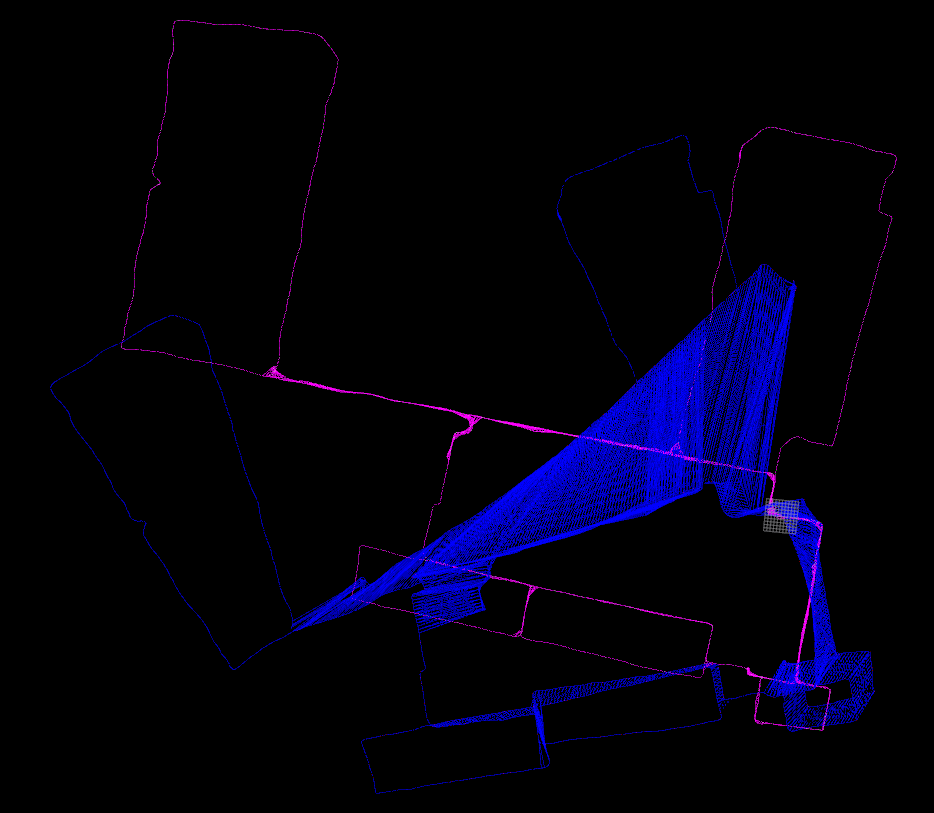
上面是一个实际激光雷达优化前后的例子
文章来源: blog.csdn.net,作者:月照银海似蛟龙,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/qq_32761549/article/details/123575516
- 点赞
- 收藏
- 关注作者


评论(0)