@[TOC](激光SLAM:ICP升级版本NICP(Normal ICP)原理+法向量即曲率计算代码)

NICP(Normal ICP)匹配方法

传统ICP的缺点:
由于ICP算法在点云的匹配关系上，是计算同一坐标系下的两帧点云上的点的距离最小作为比配点，这样的计算得到匹配关系，经常是错误的，会出现将不同位置(不同物体或者不同物体部分的扫描点)点进行匹配的情况，从而陷入局部最优。

NICP基本思想:
替换原始ICP方法中的对应点匹配(point correspondences)方法;
误差项除了考虑对应点的欧氏距离之外,同时还考虑对应点法向量的角度差。
充分利用实际曲面的特征来对错误的点匹配进行滤除,主要的特征为法向量和曲率;

上图中绿色和蓝色为两次扫描,紫色线表示匹配的点,可以看出,右上角部分虽然蓝色和绿色的点在距离上重合,但是由于法向量不同,并不会建立匹配关系.

NICP点匹配规则:

• 如果没有well define的法向量,则拒绝。
• 两点间的距离大于阈值,则拒绝。
• 两点的曲率之差距大于阈值,则拒绝。
• 两点的法向量角度之差大于阈值,则拒绝。

法向量和曲率计算

该方法需要计算点云中点的法向量和曲率
计算方法如下
数学模型:

找到点pi周围半径R球形空间内的所有点Vi,然后去中心化,并构造协方差矩阵,公式如下:

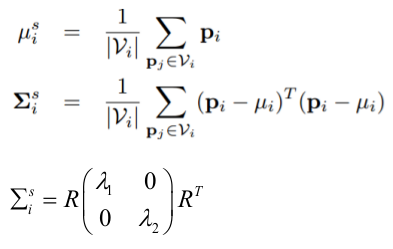
曲率的计算方法:

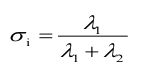
法向量的计算方法:
最小特征值对应的特征向量

上面是二维的,对于三维的则曲率计算如下:

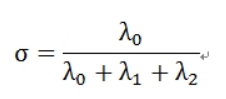
法向量依旧是最小特征值对应的特征向量
参考链接

也可以用pcl的方法求得

目标函数

传统ICP的向量是点的坐标,而NICP将其进行了扩充,即坐标+法向量.

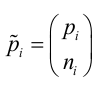
那么变换参数T(R,t)对这个扩充向量的变换则变为:

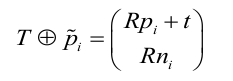
即对点进行旋转+平移,对法向量旋转.

目标函数则是点的距离和法向量角度误差

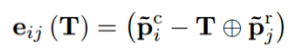
目标函数的定义为:

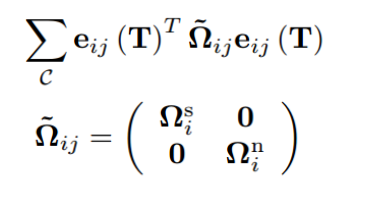
二维点云计算法向量方法 Code

通过 Eigen 的方法基于数学模型计算
完整代码

Eigen::Vector2d ComputeNormal(std::vector<Eigen::Vector2d> &nearPoints)
{
    Eigen::Vector2d normal;
    
    //根据周围的激光点计算法向量，参考ppt中NICP计算法向量的方法
    Eigen::Vector2d average;//周围点的几何中心
    average.setZero();//至0
    for(auto v : nearPoints)//遍历每个点
    {
        average += v / nearPoints.size();//求其周围点的几何中心
    }

    Eigen::Matrix2d covariance;//协方差矩阵
    covariance.setZero();//至0
    for(auto v : nearPoints)//遍历每个点
    {
        covariance += (v - average) * (v - average).transpose() / nearPoints.size();//求协方差矩阵
    }

    Eigen::EigenSolver<Eigen::Matrix2d> eigen_solver(covariance);//转化为对角线矩阵
    Eigen::Vector2d eigenValues = eigen_solver.pseudoEigenvalueMatrix().diagonal();
    Eigen::Matrix2d eigenVectors = eigen_solver.pseudoEigenvectors();
    normal = eigenValues(0) < eigenValues(1) ? eigenVectors.col(0) : eigenVectors.col(1);//计算法向量
    

    return normal;
}


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
 

代码解释

Eigen::Vector2d ComputeNormal(std::vector<Eigen::Vector2d> &nearPoints)

  

 

  
1
 

函数名称:ComputeNormal
函数功能:计算二维点云某点法向量
函数参数: nearPoints 某个点周围的所有激光点
函数返回: 该点法向量

+++++++++++++++++++++++++++++++++++++++++++++++++++++

    Eigen::Vector2d normal;//声明要计算的法向量
    
    Eigen::Vector2d average;//声明周围点的几何中心
    average.setZero();//至0

    for(auto v : nearPoints)//遍历每个点
    {
        average += v / nearPoints.size();//求其周围点的几何中心
    }


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
 

声明要计算的法向量
求其周围点的几何中心
+++++++++++++++++++++++++++++++++++++++++++++++++++++

    Eigen::Matrix2d covariance;//声明协方差矩阵
    covariance.setZero();//至0

    for(auto v : nearPoints)//遍历每个点
    {
        covariance += (v - average) * (v - average).transpose() / nearPoints.size();//求协方差矩阵
    }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
 

求协方差矩阵
就是这个公式

+++++++++++++++++++++++++++++++++++++++++++++++++++++

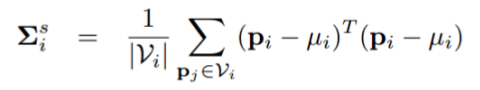
    Eigen::EigenSolver<Eigen::Matrix2d> eigen_solver(covariance);//转化为对角线矩阵
    Eigen::Vector2d eigenValues = eigen_solver.pseudoEigenvalueMatrix().diagonal();//提取特征值
    Eigen::Matrix2d eigenVectors = eigen_solver.pseudoEigenvectors();//提取特征向量构成的矩阵

  

 

  
1
  
2
  
3
 

将协方差矩阵转为对角线矩阵
提取特征值和特征向量
+++++++++++++++++++++++++++++++++++++++++++++++++++++

	normal = eigenValues(0) < eigenValues(1) ? eigenVectors.col(0) : eigenVectors.col(1);//计算法向量 : 最小特征值对应的特征向量
	
	return normal;//返回法向量

  

 

  
1
  
2
  
3
 

通过特征值和特征向量,计算该点法向量
最小特征值对应的特征向量

文章来源: blog.csdn.net，作者：月照银海似蛟龙，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/qq_32761549/article/details/123245580