激光SLAM:图优化从理论到原理推导到代码实践
激光SLAM:图优化从理论到原理推导到代码实践
图优化本身有成形的 开源的库 例如
- g2o
- ceres
- gtsam
搞SLAM的话,最好可以理解其概念,然后再用好现成的工具.本篇主要介绍图优化的基本概念.以及在RVIZ中显示位姿图的代码
Pose Graph的概念
用一个图(Graph 图论)来表示SLAM问题
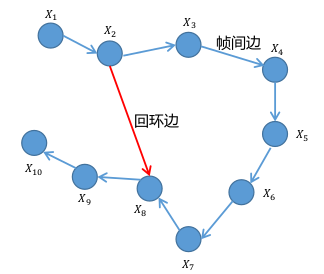
图中的节点来表示机器人的位姿 二维的话即为 (x,y,yaw)
两个节点之间的边表示两个位姿的空间约束(相对位姿关系以及对应方差或线性矩阵)
边分为了两种边
- 帧间边:连接的前后,时间上是连续的
- 回环边:连接的前后,时间上是不连续的,但是直接也是两个位姿的空间约束
构建了回环边才会有误差出现,没有回环边是没有误差的
图优化的基本思想:
出现回环边,有了误差之后.构建图,并且找到一个最优的配置(各节点的位姿),让预测与观测的误差最小
一旦形成回环即可进行优化消除误差
里程积分的相对位姿视为预测值 图上的各个节点就是通过里程(激光里程计\轮速里程计)积分得到的
回环计算的相对位姿视为观测值 图上就是说通过 X2和X8的帧间匹配作为观测值
图优化要干的事:
构建图并调整各节点的位姿,让预测与观测的误差最小
图的构建
帧间边
里程测量 得到
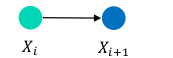
相邻节点之间的相对位姿关系,可以由里程计、IMU、帧间匹配计算得到
回环边
通过回环检测得到
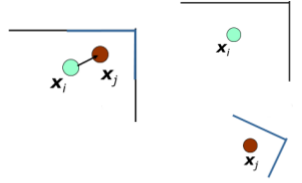
节点 i 和节点 j 在空间上相邻(观测到同样的数据),但是时间上不相邻(中间有其它节点)
用帧间匹配算法计算一个相对位姿 即为回环边的信息
一个简单的回环检测方法
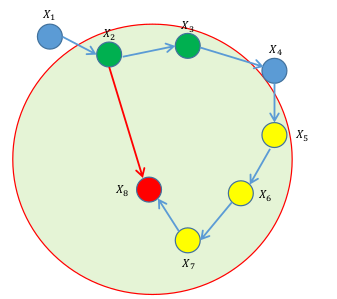
针对当前节点,如图上的X8,标为红色
把其它节点为active (黄色)和 inactive(蓝色和绿色)两部分
找到当前节点周围一定范围内所有inactive节点,作为回环候选帧(绿色节点)
周围一定范围可以认为设定一个距离比如10m,或者根据位置不确定度了设置一个距离
当前节点和回环候选帧进行匹配,根据得分(匹配的相似度)判断是否形成回环
图优化简单例程
用一个最简单的例子,走一遍图优化的过程,加深整体理解.
Pose Graph建立(机器人移动情况):
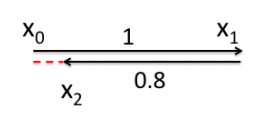
- 一个机器人,初始点在X0处,位置为0.
- 然后机器人向前移动,通过编码器测得移动距离为1,节点为X1
- 机器人向后移动,通过编码器测得移动距离为0.8,节点为X2
- 通过闭环检测,X2与X0的偏差为0
位姿图(Pose Graph)就是这样的:
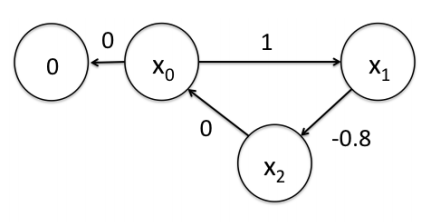
上面的例子,可以认为 编码器的测量存在误差,导致和闭环检测的结果,不一致.
那么到底机器人到了哪里,我们假如更相信闭环检测的结果,那么应该如何调整X0 X1 X2的位姿呢
就可以通过图优化的方式来进行求解.
图优化求解过程:
建立关系:
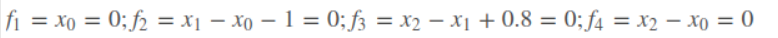
为了使总体的误差最小,使用最小二乘如下:
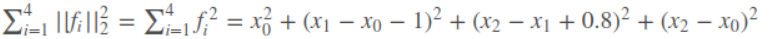
对上面的函数每个变量求偏导(雅克比矩阵),并使得偏导等于0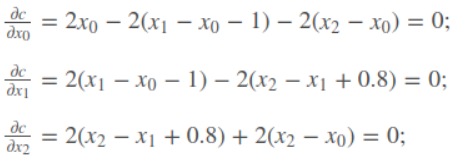
这里既可以算出 x0 x1 和x2的值为:
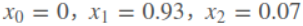
即对整体进行了优化,使得误差项最小.
Pose Graph rivz显示
Code
下面的代码通过rviz将 建立的 Pose Graph 显示出来 ,方便进行 算法的调试
是通过 rviz的 MarkerArray 形式 来 展示 的. 写成了一个函数的形式,方便使用
/***
****函数名称: PublishGraphForVisulization
****函数形参: pub 要发布的topic句柄 Vertexs 存的顶点向量 Edges 存的边的向量 color 颜色设置
****函数返回: 无
****函数功能: 在rviz中 查看 POSE graph 以MarkerArray的形式
****/
void PublishGraphForVisulization(ros::Publisher* pub,
std::vector<Eigen::Vector3d>& Vertexs,
std::vector<Edge>& Edges,
int color = 0)
{
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
函数名称: PublishGraphForVisulization
函数形参: pub 要发布的topic句柄 Vertexs 存的顶点向量 Edges 存的边的向量 color 颜色设置
函数返回: 无
函数功能: 在rviz中 查看 POSE graph 以MarkerArray的形式
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 分割线
visualization_msgs::MarkerArray marray; //声明要发布的 MarkerArray
//point--red
visualization_msgs::Marker m; //声明一个maker 用来 画出 顶点
//赋值顶点的 marker的 基本信息 初始化位置 为 0
m.header.frame_id = "map";
m.header.stamp = ros::Time::now();
m.id = 0;
m.ns = "ls-slam";
m.type = visualization_msgs::Marker::SPHERE;
m.pose.position.x = 0.0;
m.pose.position.y = 0.0;
m.pose.position.z = 0.0;
m.scale.x = 0.1;
m.scale.y = 0.1;
m.scale.z = 0.1;
//根据传入的形参 设置 顶点的颜色
if(color == 0)
{
m.color.r = 1.0;
m.color.g = 0.0;
m.color.b = 0.0;
}
else
{
m.color.r = 0.0;
m.color.g = 1.0;
m.color.b = 0.0;
}
m.color.a = 1.0;
m.lifetime = ros::Duration(0);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
声明要发布的 MarkerArray
声明一个maker 用来 画出 顶点
赋值顶点的 marker的 基本信息 初始化位置 为 0
根据传入的形参 设置 顶点的颜色
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 分割线
//linear--blue
visualization_msgs::Marker edge; //声明一个marker 用来画出边
//赋值边的 marker的 基本信息 初始化位置 为 0
edge.header.frame_id = "map";
edge.header.stamp = ros::Time::now();
edge.action = visualization_msgs::Marker::ADD;
edge.ns = "karto";
edge.id = 0;
edge.type = visualization_msgs::Marker::LINE_STRIP;
edge.scale.x = 0.1;
edge.scale.y = 0.1;
edge.scale.z = 0.1;
//根据传入的形参 设置 边的颜色
if(color == 0)
{
edge.color.r = 0.0;
edge.color.g = 0.0;
edge.color.b = 1.0;
}
else
{
edge.color.r = 1.0;
edge.color.g = 0.0;
edge.color.b = 1.0;
}
edge.color.a = 1.0;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
声明一个marker 用来画出边
赋值边的 marker的 基本信息 初始化位置 为 0
根据传入的形参 设置 边的颜色
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 分割线
m.action = visualization_msgs::Marker::ADD;
uint id = 0;
//加入节点
for (uint i=0; i<Vertexs.size(); i++)//遍历顶点
{
//遍历每个顶点 将位置赋值
m.id = id;
m.pose.position.x = Vertexs[i](0);
m.pose.position.y = Vertexs[i](1);
marray.markers.push_back(visualization_msgs::Marker(m));//puse 该 maker
id++;
}
//加入边
for(int i = 0; i < Edges.size();i++)
{
//遍历每个边 将位置赋值
Edge tmpEdge = Edges[i];
edge.points.clear();
geometry_msgs::Point p;
p.x = Vertexs[tmpEdge.xi](0);
p.y = Vertexs[tmpEdge.xi](1);
edge.points.push_back(p);
p.x = Vertexs[tmpEdge.xj](0);
p.y = Vertexs[tmpEdge.xj](1);
edge.points.push_back(p);
edge.id = id;
marray.markers.push_back(visualization_msgs::Marker(edge));
id++;
}
pub->publish(marray);//发布 以MarkerArray
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
遍历每个顶点 将位置赋值
遍历每个边 将位置赋值
发布 以MarkerArray
函数完毕,调用方式如下
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 分割线
int main(int argc, char **argv)
{
ros::init(argc, argv, "pose_graph");//初始化节点
ros::NodeHandle nodeHandle;//声明句柄
// beforeGraph 声明一个publisher
ros::Publisher beforeGraphPub;
beforeGraphPub = nodeHandle.advertise<visualization_msgs::MarkerArray>("beforePoseGraph",1,true);
// 设置 路径
std::string VertexPath = "/home/jone/ros_slam_ws/src/data/test_v.dat";
std::string EdgePath = "/home/jone/ros_slam_ws/src/data/test_e.dat";
std::vector<Eigen::Vector3d> Vertexs;//声明顶点
std::vector<Edge> Edges;//声明边
ReadVertexInformation(VertexPath,Vertexs);//读取顶点
ReadEdgesInformation(EdgePath,Edges);//读取边
//调用 rivz poes graph 显示功能函数
PublishGraphForVisulization(&beforeGraphPub,
Vertexs,
Edges);
ros::spin();
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
Result
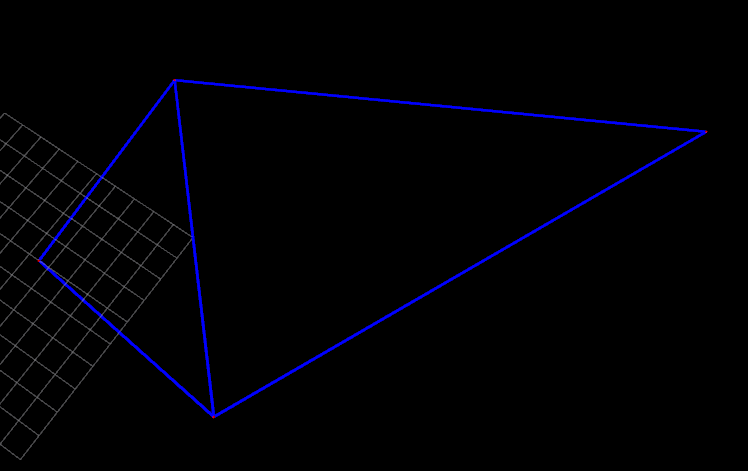
顶点的设置是这样的

边的设置是这样的

上面是一个用来测试的,例子
下面是实际工程中的数据的样子.

有了pose graph 的显示功能,可以很直观的 看到哪里建立了回环.
非线性最小二乘原理
构建完图后,就要进行图优化的过程
图优化的过程就是解决一个非线性最小二乘的过程
给定一个系统,其状态方程为:
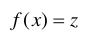
x表示系统的状态向量—即需要估计的值(slam 里面就是机器人的位姿);
z表示系统的观测值,可以通过传感器进行直接观测;
f(x)表示一个非线性的映射函数,状态向量x可以通过非线性函数f(x)映射得到z。
理想情况下,系统的状态向量(x)经过映射函数后的预测值,和观测值是相等的.但是由于测量存在噪声,会造成 状态向量不准从而预测值不准,或者观测值不准.造成不相等.那么非线性最小二乘就是通过估计状态向量x,使得其经过f(x)映射之后的预测值和观测值的误差最小.
示意图如下:
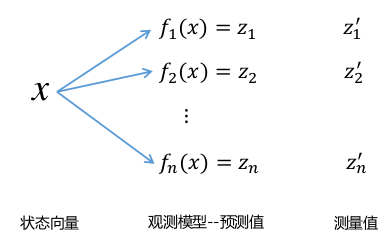
- x 表示机器人的位置
- f(x) 为观测模型,节点之间相对位姿计算函数
- z’ 为帧间匹配或者回环检测计算出来的相对位姿
- 找到最优的x,让预测和观测的误差最小
误差函数构建:
目标为最小化预测和观测的差,因此误差即为预测和观测的差:
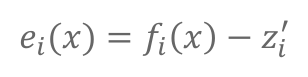
观测值误差服从高斯分布,则误差函数ei(x)也服从高斯分布.
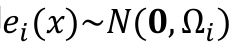
Ωi 为对应的信息矩阵。
那么误差的联合概率分布为:(固定公式–高斯的密度函数)
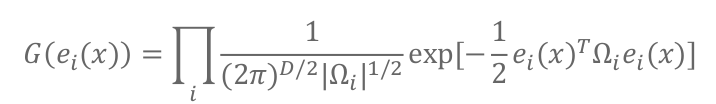
最终目标是使得误差尽可能趋近于0(均值)-----等价于每个高斯分布取得最大值,
就是上面那个公式的G(ei(x))取得最大值.(但是那个公司那么复杂,又是连乘和指数),要做一个变形,两边取ln,函数的单调性不变嘛,连乘则变为连加,成为下面形式:
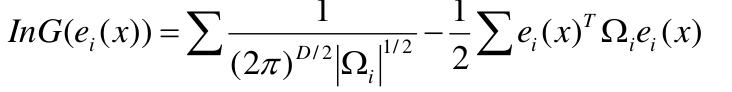
求lnG(ei(x))的最大值,那么前面的分数是和x没关系的可以去掉,就剩下-1/2和后面那部分,也就是后面那部分的最小值.
令非线性最小二乘的目标函数为:
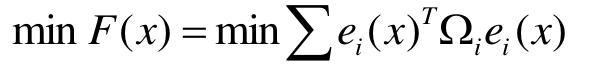
好了,现在得到了最终要求得目标函数
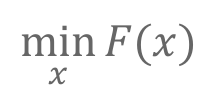
直接想法:求F(x)关于变量x的导数,令其等于0,求解方程即可。
对于凸函数来说,上述想法是可行的,但对于非凸函数(因为求完导还是非线性的),通常采用基于**梯度(本质就是把非线性函数线性化)**的优化方法。
那么下面就需要将F(x)线性化,用到的方法就是----泰勒展开
F(x)线性化:
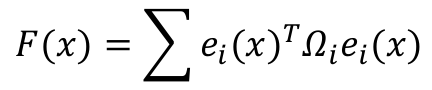
误差函数ei(x)是非线性函数,因此F(x)是关于x的非线性函数。
对误差函数ei(x)进行线性化,那么F(x)也就成了线性函数.对误差函数ei(x)进行线性化得到(泰勒展开的一阶近似公式):
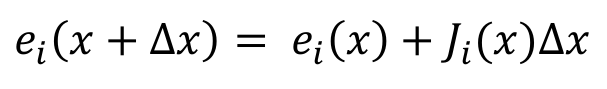
其中,J为映射函数F(x)对状态向量x的导数,称之为Jacobian(雅克比)矩阵。
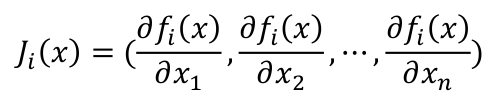
因此,函数F(x)的可化解为:
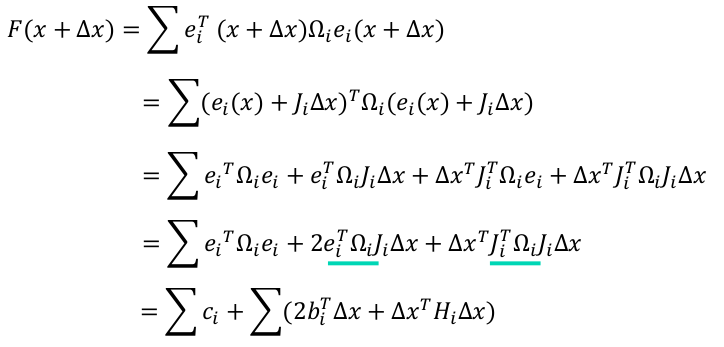
下面逐行解释上面的化解过程:
- 第一行到第二行就是把泰勒公式的一阶展开公式带入
- 第二行到第三行就是把括号里的相乘展开
- 第三行到第四行就是将中间的两项,合为一项,能合为一项的原因就是 两项都是一个数 ,然后互为转置,所有两项相等
- 第四行到第五行就是把复杂的和x每什么关系的用其它字母表示了

然后继续,可以看到上面F(x + ∆x)化成的第五行形式,是关于变量∆x的二次函数,这个是个凸函数了
要求F(x + ∆x)的最小值时,x的值,即令其关于∆x的导数等于0,此时即可得到∆x的值.为了更好的求∆x的偏导,我们继续化简F(x + ∆x)

第一行变成第二行就是把连加的符合内与连加没有关系的项提了出来
第二行变成第三行就是是把连加的部分有一个字母表示,只是看起来方便
到这里可以更方便的看出F(x + ∆x)是关于变量∆x的二次函数
求偏导得到:
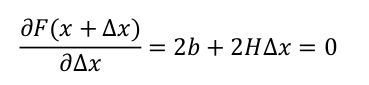
可以得到∆x为:
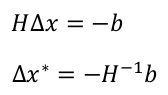
令x = x + ∆x∗ ,然后不断迭代,直至收敛即可。
这个∆x即为下降的梯度.
至此一个非线性最小二乘问题就得到了求解!
总结下上面的流程:
1 线性化误差函数:
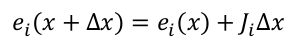
2 构建线性系统:
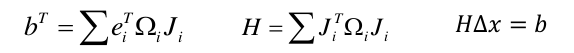
3 求解线性系统:
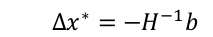
4 更新解,并不断迭代直至收敛:
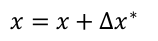
测试Code
上面理论上推导到非线性最小二乘的原理和解法.下面通过Code进行测试.
#include <iostream>
#include <opencv2/opencv.hpp>
#include <Eigen/Core>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main(int argc, char **argv) {
double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值
double ae = 2.0, be = -1.0, ce = 5.0; // 估计参数值
int N = 100; // 数据点
double w_sigma = 1.0; // 噪声Sigma值
double inv_sigma = 1.0 / w_sigma;
cv::RNG rng;
// OpenCV随机数产生器
vector<double> x_data, y_data; // 数据
for (int i = 0; i < N; i++) {
double x = i / 100.0;
x_data.push_back(x);
y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
}
// 开始Gauss-Newton迭代
int iterations = 100; // 迭代次数
double cost = 0, lastCost = 0; // 本次迭代的cost和上一次迭代的cost
for (int iter = 0; iter < iterations; iter++) {
Matrix3d H = Matrix3d::Zero(); // Hessian = J^T W^{-1} J in Gauss-Newton
Vector3d b = Vector3d::Zero(); // bias
cost = 0;
for (int i = 0; i < N; i++) {
double xi = x_data[i], yi = y_data[i]; // 第i个数据点
double error = yi - exp(ae * xi * xi + be * xi + ce);
Vector3d J; // 雅可比矩阵
J[0] = -xi * xi * exp(ae * xi * xi + be * xi + ce); // de/da
J[1] = -xi * exp(ae * xi * xi + be * xi + ce); // de/db
J[2] = -exp(ae * xi * xi + be * xi + ce); // de/dc
H += inv_sigma * inv_sigma * J * J.transpose();
b += -inv_sigma * inv_sigma * error * J;
cost += error * error;
}
// 求解线性方程 Hx=b
Vector3d dx = H.ldlt().solve(b);
if (isnan(dx[0])) {
cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost >= lastCost) {
cout << "cost: " << cost << ">= last cost: " << lastCost << ", break." << endl;
break;
}
ae += dx[0];
be += dx[1];
ce += dx[2];
lastCost = cost;
cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() <<
"\t\testimated params: " << ae << "," << be << "," << ce << endl;
}
cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
非线性最小二乘在图优化SLAM中的应用
非线性最小二乘在 SLAM领域和机器人状态估计领域应用的非常广泛
流程都是差不多的.像g2o ceres gtsam 实际上就是通用的库,本质都是求非线性最小二乘
误差函数
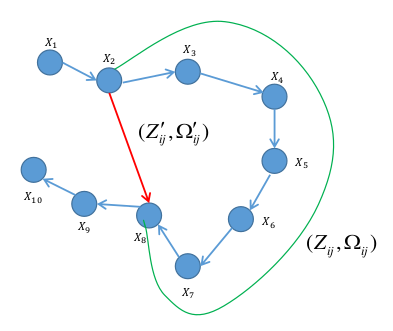
还是按上面这个图:
1 观测值为匹配计算得到的节点i和节点j的相对位姿,就是红色的那个边
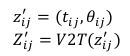
2 预测值为里程积分得到的当前节点i和节点j的相对位姿,就是绿色的那个形成的边.
每个节点都有一个相对于世界坐标系的位姿,位姿由上一节点积分来,所以可以直接用i和j的位姿求相对位姿:
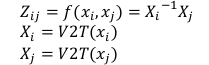
3 误差函数的定义:
相对观测值有个相对位姿,预测值有个相对位姿,那么这两个相对位姿之间的偏差是多少呢?
就是求两个相对位姿的相对位姿,也就是:
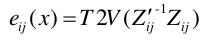
上面这个是误差函数的抽象表达式,那么精确表达式则是下面这种
首先已知每个点的位姿矩阵
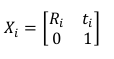
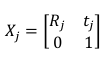
则预测值的相对位姿为:
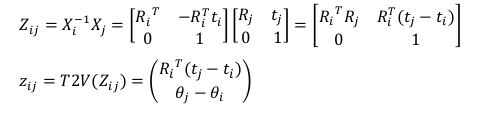
测量值的相对位姿是由Rij和tij构成,按照上面的推论,则误差函数的向量形式
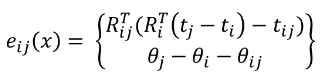
然后就是求 Jacobian(雅克比矩阵):
就是对误差函数的向量分别求xi和xj的偏导
求xi的偏导:
xi由(ti,θi)构成,所有
1 误差向量的第一行对ti求导, 结果:
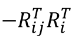
放到矩阵的1,1位置
2 误差向量的第一行对θi求导, 结果:
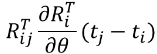
放到矩阵的1,2位置
3 误差向量的第二行对ti求导, 结果:
0
放到矩阵的2,1位置
4 误差向量的第二行对θi求导, 结果:
-1
放到矩阵的2,2位置
所以误差向量对xi求偏导的结果是:
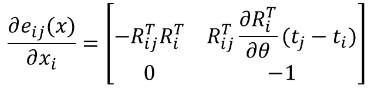
同理误差向量对xj求偏导的结果是:
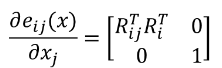
现在有了误差函数和雅克比矩阵
(上面的误差函数是通过变换矩阵计算相对位姿然后再转为向量形式,也可以直接用向量形式相减 gtsam是这样的)
上面的操作构建了误差函数并线性化,然后求得了雅克比矩阵:
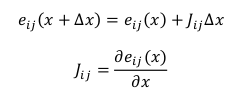
这里要注意一个性质:
误差函数只跟xi 和xj 有关,x是一个多维的,可以是很大的比如1000维,但是求完偏导后除了xi和xj其它位置都为0
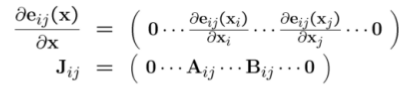
Jacobian矩阵的形式,图形化就是下面这样的:
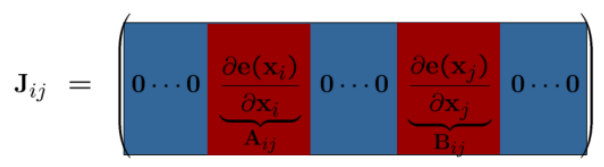
这样的形式,可以说是一个稀疏的向量.
推导非线性最小二乘的时候构建H矩阵的公式是:
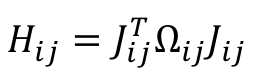
所以H也是一个稀疏的矩阵
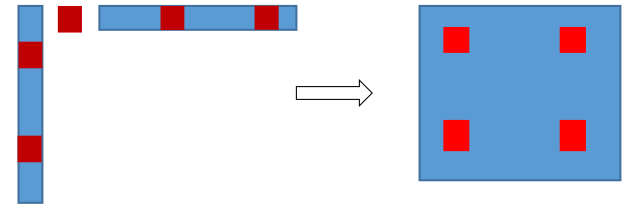
向量里仅有两项非0,那么矩阵里就只有4项非0
同理bij也是稀疏的
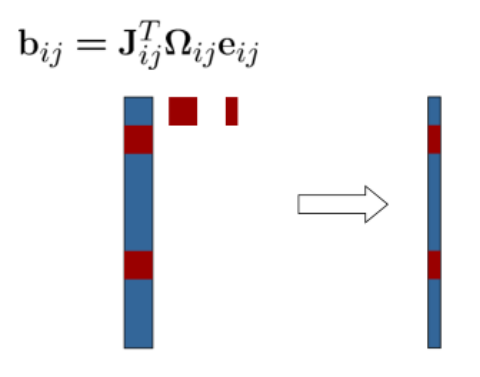
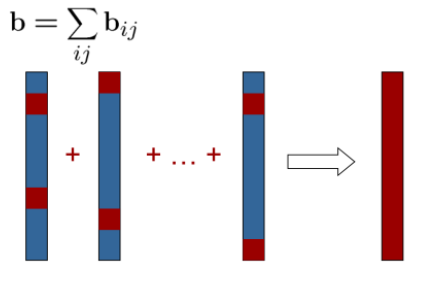
H和b最终都是和的形式,
b最后是稠密的,形式如下:
H最后是稀疏的,形式如下:
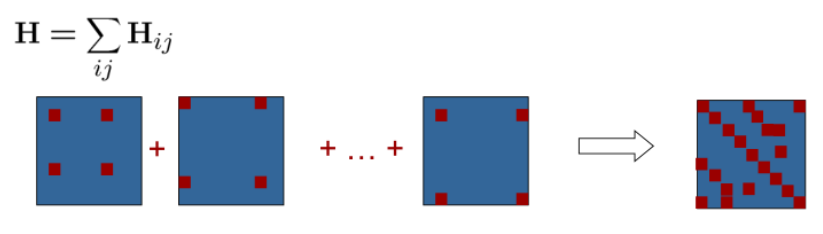
为什么要特意强调H矩阵是稀疏的呢?
H 矩阵为稀疏矩阵,可以利用此特征进行快速求解。这因为如此,才有了开源库,使得非线性最小二乘在图优化里面有了成熟的应用.
在算∆x的时候是要求H的逆的
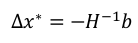
如果H不是稀疏的话,1000维的H,求其逆耗费的运算量是非常大的
有了H矩阵和b矩阵,那么非线性最小二乘就可以解了,然后就是不断迭代了.
以上整个过程的推导总结下使用方法:
构建线性系统:
- 已知误差项eij和Jacobian矩阵Aij 和Bij
- 向量b更新

- 矩阵H更新

求解线性系统: - 已知矩阵H和向量b
- 求解线性方程组

- 不断进行迭代,直至收敛

x即为优化后的结果
代码实践–基于非线性最小二乘的slam优化
位姿向量转换成变换矩阵
在公式中经常需要把位姿向量转换成变换矩阵,例如:
观测值为匹配计算得到的节点i和节点j的相对位姿:
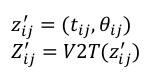
这里的第二行V2T的公式就是把位姿向量转换成变换矩阵.
代码写成函数的形式,方便后面调用.
//位姿向量-->转换矩阵
//函数形参 : 位姿向量 x,y,θ
//函数返回 : 变换矩阵
Eigen::Matrix3d PoseToTrans(Eigen::Vector3d x)
{
Eigen::Matrix3d trans;//声明转换矩阵
trans << cos(x(2)),-sin(x(2)),x(0),
sin(x(2)), cos(x(2)),x(1),
0, 0, 1;
return trans;//返回转换矩阵
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
变换矩阵转换成位姿向量
同样也有把变换矩阵转换成位姿向量的形式,例如:
将观测值和预测值的两个相对位姿计算误差函数的时候
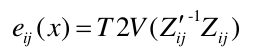
这里的第二行T2V公式就是把变换矩阵转换成位姿向量.
代码写成函数的形式,方便后面调用.
//函数功能 : 转换矩阵-->位姿向量
//函数形参 : 转换矩阵 3*3
//函数返回 : 位姿向量
Eigen::Vector3d TransToPose(Eigen::Matrix3d trans)
{
Eigen::Vector3d pose;//声明位姿向量
pose(0) = trans(0,2);
pose(1) = trans(1,2);
pose(2) = atan2(trans(1,0),trans(0,0));
return pose;//返回位姿向量
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
计算误差向量和Jacobian
下面完成 当点i(xi)与点j(xj)和两个点的观测值(z)[匹配的结果] 后 计算出误差向量(ei)和Jacobian矩阵里的Ai和Bi,有了这三个量就可以计算出b和H矩阵,这个计算在其它函数中进行,首先看ei Ai Bi的计算函数:

红框里的就是要求的三个量,为什么是这个公式,在前面推导了
/**
* 函数名称: CalcJacobianAndError
* 函数功能: 计算jacobian矩阵和error
* @param xi fromIdx
* @param xj toIdx
* @param z 观测值:xj相对于xi的坐标
* @param ei 计算的误差
* @param Ai 相对于xi的Jacobian矩阵
* @param Bi 相对于xj的Jacobian矩阵
*/
void CalcJacobianAndError(Eigen::Vector3d xi,Eigen::Vector3d xj,Eigen::Vector3d z,
Eigen::Vector3d& ei,Eigen::Matrix3d& Ai,Eigen::Matrix3d& Bi)
{
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
函数名称和形参这样设置
由于已知 xi xj z,那么公式里的ti tj θi θj θij 均已知了,那么剩下的就是R的那几个矩阵了
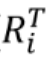
Eigen::Matrix2d RiT;//声明 Ri转置矩阵
RiT << cos(xi(2)),sin(xi(2)),
-sin(xi(2)),cos(xi(2));//赋值
- 1
- 2
- 3
正常的姿态矩阵是:

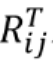
Eigen::Matrix2d RijT;//声明 Rij转置矩阵
RijT << cos(z(2)),sin(z(2)),
-sin(z(2)),cos(z(2));//赋值
- 1
- 2
- 3
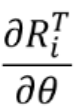
Eigen::Matrix2d dRiT;//声明 Ri 对θ求导的矩阵
dRiT << -sin(xi(2)), cos(xi(2)),
-cos(xi(2)),-sin(xi(2));//赋值
- 1
- 2
- 3
cos的导数是-sin ,sin的导数是cos,所以矩阵就是上面的形式了.
公式里面的所有量都已知了,剩下的就是计算了.
/*ei的计算*/
ei.block(0, 0, 2, 1) = RijT * (RiT * (xj.block(0, 0, 2, 1) - xi.block(0, 0, 2, 1)) - z.block(0, 0, 2, 1));//公式
ei(2) = xj(2) - xi(2) - z(2);//公式
//将角度 限制在 -pi ~ pi
if (ei(2) > M_PI)
ei(2) -= 2 * M_PI;
else if (ei(2) < -M_PI)
ei(2) += 2 * M_PI;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
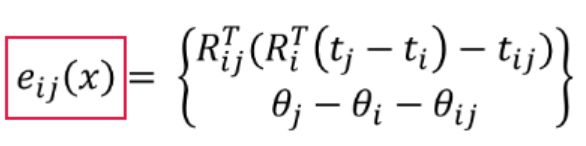
ei的计算,没啥好说的,就是公式带入.最后注意限制角度的范围
/*Ai和Bi的计算*/
Ai.block(0, 0, 2, 2) = - RijT * RiT;//公式
Ai.block(0, 2, 2, 1) = RijT * dRiT * (xj.block(0, 0, 2, 1) - xi.block(0, 0, 2, 1));//公式
Ai.block(2, 0, 1, 3) << 0, 0, -1;//公式
Bi.setIdentity();
Bi.block(0, 0, 2, 2) = RijT * RiT;//公式
- 1
- 2
- 3
- 4
- 5
- 6
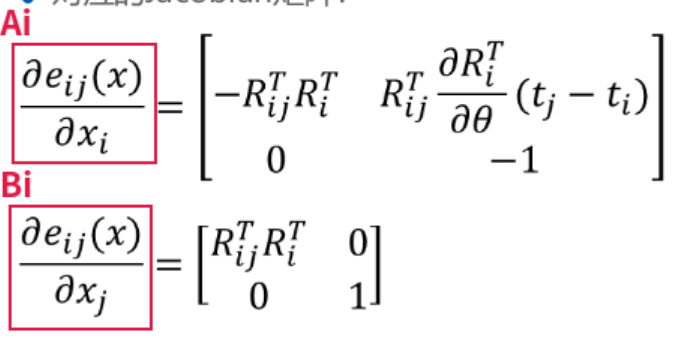
对应公式带入
然后这个函数就完了
一次迭代求解
现在有了一条边的 eij和Ai Bi ,下面需要遍历每条边,生成H和b矩阵,然后就可以求到dx了.一次迭代就完了.下面完成这部分的代码
/**
* @函数名称: LinearizeAndSolve
* @函数功能: 高斯牛顿方法的一次迭代.
* @param Vertexs 图中的所有节点
* @param Edges 图中的所有边
* @return dx 位姿的增量
*/
Eigen::VectorXd LinearizeAndSolve(std::vector<Eigen::Vector3d>& Vertexs,
std::vector<Edge>& Edges)
{
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
函数名称和形参这样设置
//申请内存
Eigen::MatrixXd H(Vertexs.size() * 3,Vertexs.size() * 3);//H矩阵的维度 (点个数*单点纬度) * (点个数*单点纬度)
Eigen::VectorXd b(Vertexs.size() * 3);//b矩阵的维度 (点个数*单点纬度)
H.setZero();//至零
b.setZero();//至零
//固定第一帧
Eigen::Matrix3d I;
I.setIdentity();
H.block(0,0,3,3) += I;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
首先声明H矩阵和b矩阵
H矩阵的维度 (点个数 * 单点纬度) * (点个数 * 单点纬度) 二维的话单点维度就是3 (x,y,θ)
b矩阵的维度 (点个数*单点纬度)
固定第一帧是为了初始化一个固定的位置
//构造H矩阵 & b向量
for(int i = 0; i < Edges.size();i++)
{
//提取信息
Edge tmpEdge = Edges[i];
Eigen::Vector3d xi = Vertexs[tmpEdge.xi];
Eigen::Vector3d xj = Vertexs[tmpEdge.xj];
Eigen::Vector3d z = tmpEdge.measurement;
Eigen::Matrix3d infoMatrix = tmpEdge.infoMatrix;
//计算误差和对应的Jacobian
Eigen::Vector3d ei;
Eigen::Matrix3d Ai;
Eigen::Matrix3d Bi;
CalcJacobianAndError(xi,xj,z,ei,Ai,Bi);
//TODO--Start
b.block(3*tmpEdge.xi, 0, 3, 1) += Ai.transpose() * infoMatrix * ei;
b.block(3*tmpEdge.xj, 0, 3, 1) += Bi.transpose() * infoMatrix * ei;
H.block(3*tmpEdge.xi, 3*tmpEdge.xi, 3, 3) += Ai.transpose() * infoMatrix * Ai;
H.block(3*tmpEdge.xi, 3*tmpEdge.xj, 3, 3) += Ai.transpose() * infoMatrix * Bi;
H.block(3*tmpEdge.xj, 3*tmpEdge.xi, 3, 3) += Bi.transpose() * infoMatrix * Ai;
H.block(3*tmpEdge.xj, 3*tmpEdge.xj, 3, 3) += Bi.transpose() * infoMatrix * Bi;
//TODO--End
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
这部分遍历每个边,去构造H矩阵和b矩阵实际的地方
循环里的第一部分先提取边里的信息,预测值:xi xj 测量值:z 信息矩阵:infoMatrix
然后第二部分用上一环境构造的函数计算ei Ai Bi
第三部分用ei Ai Bi去构造H和b矩阵,添加到相应位置,就按照下面的公式:


//求解
Eigen::VectorXd dx;//声明dx
dx = H.colPivHouseholderQr().solve(-b);//有了H和b即可以求解dx
return dx;//返回dx
}
- 1
- 2
- 3
- 4
- 5
遍历完每条边,那么H和b矩阵就构造完了,即可求出dx并返回该值,完成一次迭代求解.
完成图优化功能
接下来写一个迭代的循环,不断调用一次迭代求解的这个函数,完成图优化功能.
int maxIteration = 100;//最大迭代次数
double epsilon = 1e-4;//精度要求阈值
for(int i = 0; i < maxIteration;i++)//迭代求解
{
std::cout <<"Iterations:"<<i<<std::endl;//输出迭代的次数
Eigen::VectorXd dx = LinearizeAndSolve(Vertexs,Edges);//一次的迭代求解
//进行位姿更新 将上面求解的dx叠加到x上
for(int j = 0; j < Vertexs.size(); ++j)
{
//更新x
Vertexs[j](0) += dx(j*3);
Vertexs[j](1) += dx(j*3+1);
Vertexs[j](2) += dx(j*3+2);
//限制角度
if (Vertexs[j](2) > M_PI)
Vertexs[j](2) -= 2 * M_PI;
else if (Vertexs[j](2) < -M_PI)
Vertexs[j](2) += 2 * M_PI;
}
double maxError = -1;//迭代过程中的dx中的最小值
for(int k = 0; k < 3 * Vertexs.size();k++)
{
if(maxError < std::fabs(dx(k)))
{
maxError = std::fabs(dx(k));
}
}
if(maxError < epsilon)//精度满足要求则跳出优化
break;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
通过一个for循环,不断迭代,不断调用一次迭代求解的这个函数,完成图优化功能.
一个判断精度是否满足要求的判断,精度满足要求或者达到最大的迭代次数后,则作为最终的优化结果.
位姿图显示
在进行优化前,可以调用之前写的rviz显示位姿图的函数,来可视化优化前后的结果
//调用 rivz poes graph 显示功能函数
PublishGraphForVisulization(&beforeGraphPub,
Vertexs,
Edges);
- 1
- 2
- 3
- 4
PublishGraphForVisulization(&afterGraphPub,
Vertexs,
Edges,1);
- 1
- 2
- 3
Result
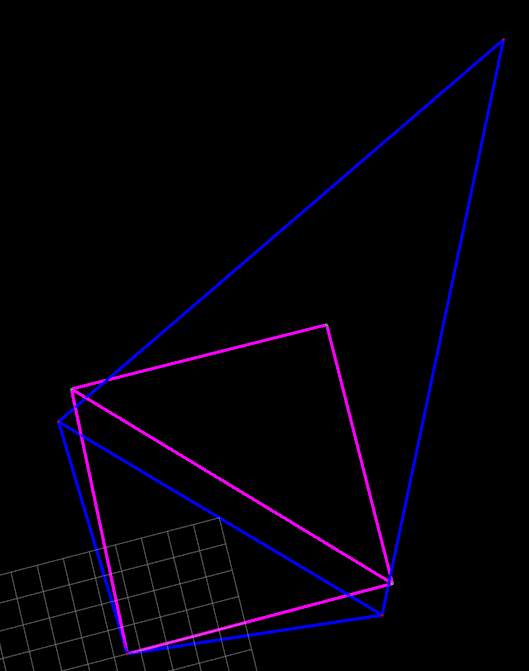
上面是一个测试用的位姿图例子,仅有四个点,五个边
蓝色的是图优化前的位姿图
粉色的是图优化后的位姿图
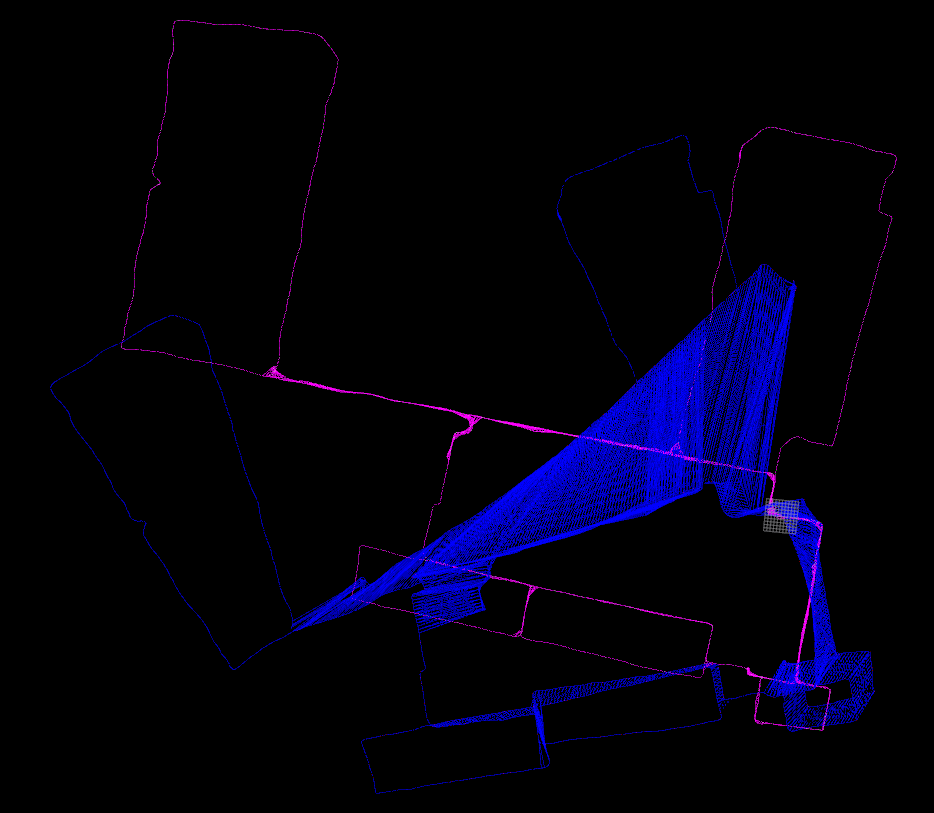
上面是一个实际激光雷达优化前后的例子
文章来源: blog.csdn.net,作者:月照银海似蛟龙,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/qq_32761549/article/details/123257340
- 点赞
- 收藏
- 关注作者

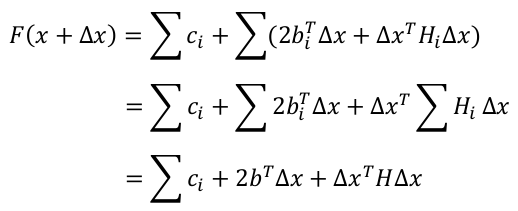


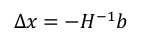
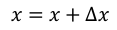

评论(0)