前言

ICP全称 Iterative Closest Point ,翻译过来就是迭代最近点.ICP在点云配准领域应用的非常广泛,因此基于深度相机\激光雷达的算法使用ICP的频率比较高.

ICP的目的是用来求解两个点云集合转换关系,也是目前的最通用的方法。

最基本的ICP是通过对应点去求解点云的对应关系,后期演变出点线ICP\点面ICP等等众多的方法.

本篇博客主要来探究下ICP家族的师祖,点点ICP的数学模型,及推导.最后用代码证明.

ICP数学模型

给定两个点云集合:

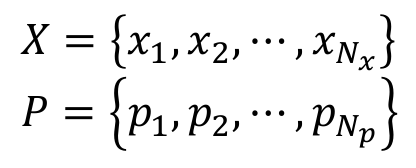
xi和pi表示点云的坐标;
Nx和Np表示点云的数量.
ICP的核心思想是:
求解旋转矩阵R和平移向量t,使得下式最小:

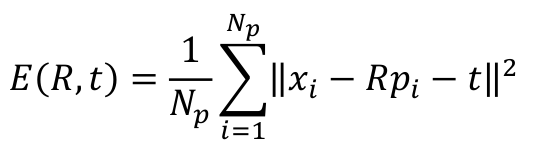
ICP求解方法

在已知对应点的情况下.就是说上面的x1和p1对应,x2和p2对应…

进行两个点云的去中心化

求x点云的几何中心坐标

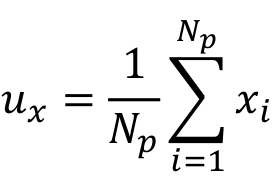
求p点云的几何中心坐标

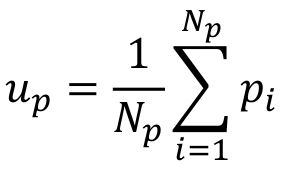
两个点云分别每个点减去各自的点云几何中心坐标,形成新的点云

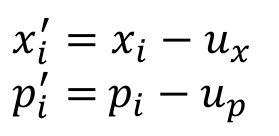
求W矩阵并进行SVD分解

将上面的新形成的两个点云相乘(其中一个先转置)得到的矩阵为W矩阵
然后对W矩阵进行SVD分解,得到U和V矩阵

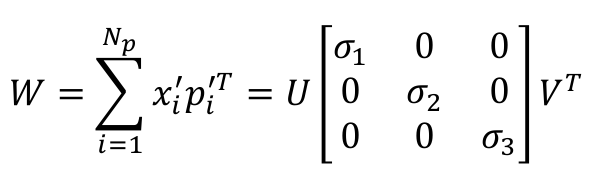
计算R和t

通过U和V即可计算出R
然后通过两个点云的中心坐标及R可算出t

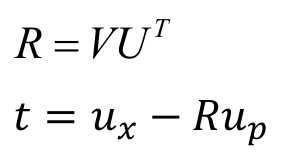
求解方法公式推导

从上面说的核心公式开始

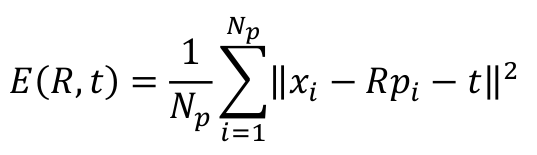
引入点云的几何中心ux和up,由于核心公式里pi前乘了R,所以up前也乘R才好合并.下式红色部分为0

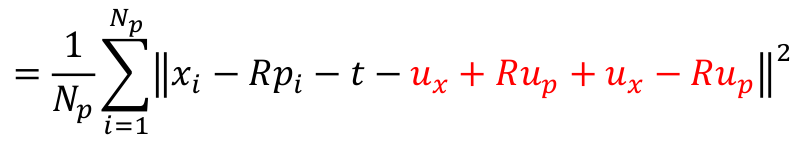
把中心点移到前面,剩下的和t组成最后括号里的

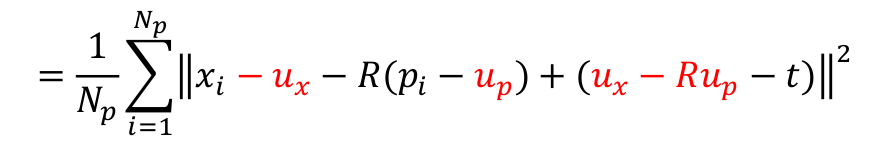
将平方开出来,形成,下面的式子

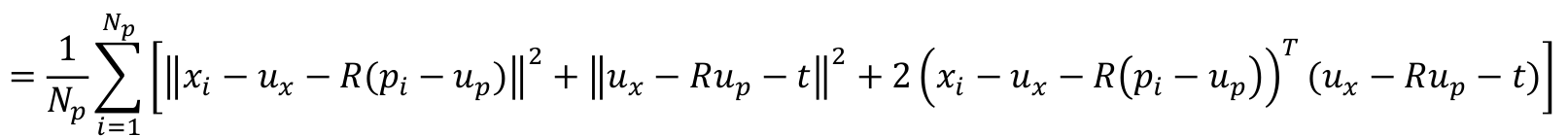
这个式子中红色框是为0的.蓝色框是需要继续向下求的

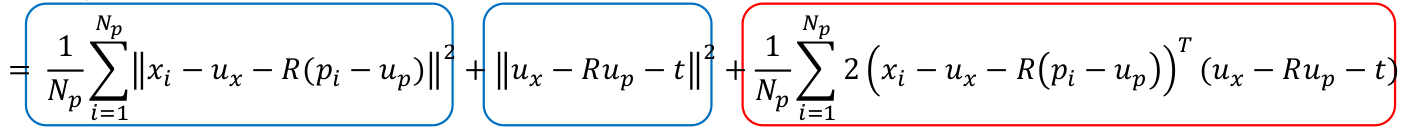
第一个蓝框仅与R有关
第二个蓝框中,对于任意R,总能得到t = ux − Rup ,使它等于0

那么原核心公式可以转换为:

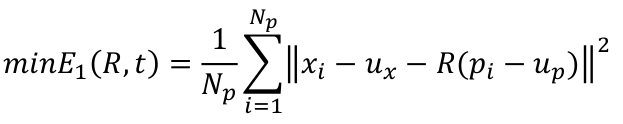
将去中心化的点云表达式引入:

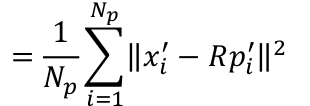
开平方得到下式

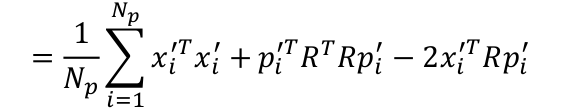
中间项的RTR就是E了,也就没R了,将有R的提出了,无R的向后放

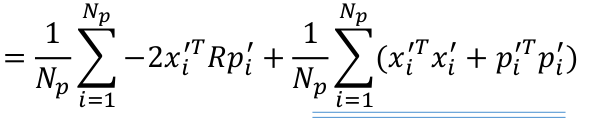
上式中画横线的是一个固定值,与R无关,所以就成了求第一项的最小值
也就是

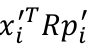
的最大值


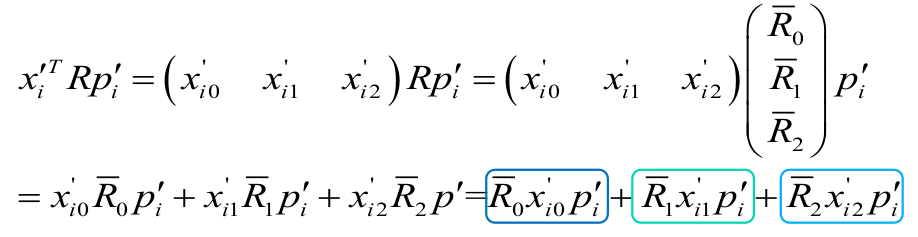
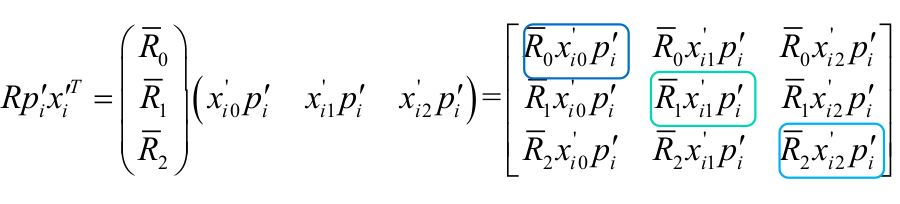
注意第一个式子和第二个的对角线元素对应一致,所以

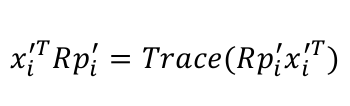
到现在核心公式转为了求下面的式子

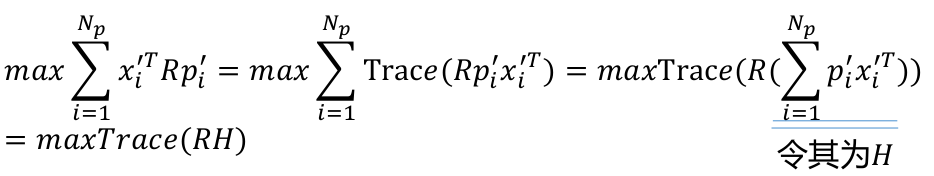
对H进行SVD分解,即

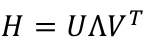
令


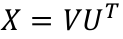
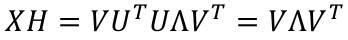
XH为正定对称矩阵.所以

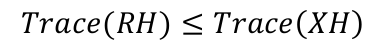
当R=X时,RH的值最大.所以R的解为

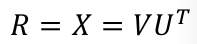
代码证明

Code

int main (int argc, char** argv)
{

        /*自己构建点云*/
        pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_in (new pcl::PointCloud<pcl::PointXYZ>);//声明源点云
        pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_out (new pcl::PointCloud<pcl::PointXYZ>);//声明目标点云
        /*自己构建的点云 */
        /*填充源点云*/
        cloud_in->width    = 100;
        cloud_in->height   = 1;
        cloud_in->is_dense = false;
        cloud_in->points.resize (cloud_in->width * cloud_in->height);
        for (size_t i = 0; i < cloud_in->points.size (); ++i)
        {   
            cloud_in->points[i].x = 1024 * rand () / (RAND_MAX + 1.0f);
            cloud_in->points[i].y = 1024 * rand () / (RAND_MAX + 1.0f);
            //cloud_in->points[i].z = 1024 * rand () / (RAND_MAX + 1.0f);
            //先测试二维数据
            cloud_in->points[i].z = 1;
        }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
 

首先构建一个原点云.里面设置100个点,然后随机取值

        /*构建变换矩阵*/
        float d_yaw = 30;//变化航向角度 单位度
        float d_x = 1;//变换平移x
        float d_y = 2;//变换平移y

        float s = sin(d_yaw*M_PI/180);
        float c = cos(d_yaw*M_PI/180);
        Eigen::Matrix3f T;//变换矩阵
        T<< c , -s , d_x,
            s , c  , d_y,
            0 , 0  , 1;

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

构建变换矩阵

        //将源点云赋值给目标点云
        *cloud_out = *cloud_in;

        /*将源点云经过变换矩阵,获得目标点云*/
        for (size_t i = 0; i < cloud_in->points.size (); ++i)
        {
            Eigen::Vector3f point_in,point_out;
            point_in << cloud_in->points[i].x,cloud_in->points[i].y,cloud_in->points[i].z;
            point_out= T * point_in;
            cloud_out->points[i].x = point_out[0];
            cloud_out->points[i].y = point_out[1];
            cloud_out->points[i].z = point_out[2];
        }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
 

将原点云经过变换矩阵得到目标点云

            /*求两个点云的几何中心*/
        int num_points = cloud_in->points.size ();
        Eigen::Vector3f sum_point_in = Eigen::Vector3f::Zero();
        Eigen::Vector3f sum_point_out = Eigen::Vector3f::Zero();
        for(size_t i=0;i<num_points;++i)
        {
            sum_point_in[0] = sum_point_in[0] + cloud_in->points[i].x ; 
            sum_point_in[1] = sum_point_in[1] + cloud_in->points[i].y ;
            sum_point_in[2] = sum_point_in[2] + cloud_in->points[i].z ;

            sum_point_out[0] = sum_point_out[0] + cloud_out->points[i].x ; 
            sum_point_out[1] = sum_point_out[1] + cloud_out->points[i].y ;
            sum_point_out[2] = sum_point_out[2] + cloud_out->points[i].z ;
        }
        Eigen::Vector3f u_point_in,u_point_out;
        //源点云几何中心
        u_point_in[0] = sum_point_in[0]/num_points;
        u_point_in[1] = sum_point_in[1]/num_points;
        u_point_in[2] = sum_point_in[2]/num_points;
        //目标点云几何中心
        u_point_out[0] = sum_point_out[0]/num_points;
        u_point_out[1] = sum_point_out[1]/num_points;
        u_point_out[2] = sum_point_out[2]/num_points;


        /*点云去中心化*/
        for(size_t i=0;i<num_points;++i)
        {
            //源点云去中心化
            cloud_in->points[i].x = cloud_in->points[i].x - u_point_in[0] ;
            cloud_in->points[i].y = cloud_in->points[i].y - u_point_in[1] ;
            cloud_in->points[i].z = cloud_in->points[i].z - u_point_in[2] ;
            //cloud_in->points[i].z = 1 ;
            //目标点云去中心化
            cloud_out->points[i].x = cloud_out->points[i].x - u_point_out[0] ;
            cloud_out->points[i].y = cloud_out->points[i].y - u_point_out[1] ;
            cloud_out->points[i].z = cloud_out->points[i].z - u_point_out[2] ;
            //cloud_out->points[i].z = 1 ;
        }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
 

求两个点云的几何中心,然后去中心化

        /*求W矩阵*/
        Eigen::Matrix3f W =Eigen::Matrix3f::Zero();//声明W矩阵
        for(size_t i=0;i<num_points;++i)
        {        
            Eigen::Vector3f point_in,point_out;
            point_in << cloud_in->points[i].x,cloud_in->points[i].y,cloud_in->points[i].z;
            point_out << cloud_out->points[i].x,cloud_out->points[i].y,cloud_out->points[i].z;

            W = W + point_out*point_in.transpose();//累加求和
           
        }

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
 

求W矩阵

        //对W矩阵进行SVD分解
        Eigen::JacobiSVD<Eigen::MatrixXf> svd(W, Eigen::ComputeThinU | Eigen::ComputeThinV );
        //求V和U
	    Eigen::Matrix3f V = svd.matrixV(), U = svd.matrixU();

  

 

  
1
  
2
  
3
  
4
 

将W矩阵进行SVD分解,然后得到U和V

        /*求R和t*/
        Eigen::Matrix3f R = U*V.transpose();//这里公式和课件里不一致
        Eigen::Vector3f t = u_point_out - R*u_point_in;
        std::cout << "R"  << std::endl<< R << std::endl;
        std::cout << "t" << std::endl << t << std::endl;

  

 

  
1
  
2
  
3
  
4
  
5
 

求R和t

Result

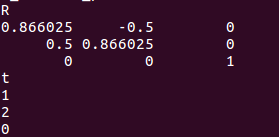
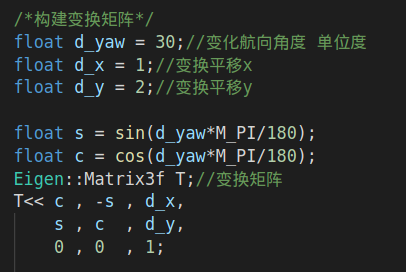
求解的结果和代码里构建的变换矩阵是一致的

文章来源: blog.csdn.net，作者：月照银海似蛟龙，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/qq_32761549/article/details/122538257