slam中的图优化的环节,本质上实际是一个非线性最小二乘问题的求解过程.本篇则探究下:

• 非线性最小二乘问题的构建
• 非线性最小二乘问题的求解
• 非线性最小二乘问题的求解原理
• Code验证理论

slam中的图优化的位姿图构建构建即理论在上一篇博客,链接

构建完图后,就要进行图优化的过程
图优化的过程就是解决一个非线性最小二乘的过程

非线性最小二乘问题的构建

给定一个系统,其状态方程为:

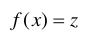
x表示系统的状态向量—即需要估计的值(slam 里面就是机器人的位姿);
z表示系统的观测值,可以通过传感器进行直接观测;
f(x)表示一个非线性的映射函数,状态向量x可以通过非线性函数f(x)映射得到z。

理想情况下,系统的状态向量(x)经过映射函数后的预测值,和观测值是相等的.但是由于测量存在噪声,会造成 状态向量不准从而预测值不准,或者观测值不准.造成不相等.那么非线性最小二乘就是通过估计状态向量x,使得其经过f(x)映射之后的预测值和观测值的误差最小.

示意图如下:

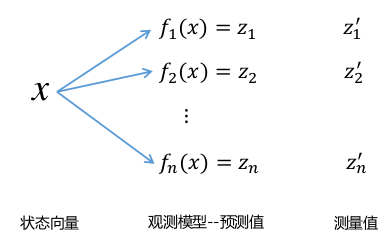
• x 表示机器人的位置
• f(x) 为观测模型,节点之间相对位姿计算函数
• z’ 为帧间匹配或者回环检测计算出来的相对位姿
• 找到最优的x,让预测和观测的误差最小

误差函数构建:
目标为最小化预测和观测的差,因此误差即为预测和观测的差:

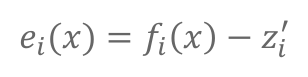
观测值误差服从高斯分布,则误差函数ei(x)也服从高斯分布.

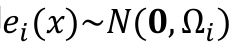
Ωi 为对应的信息矩阵。
那么误差的联合概率分布为:(固定公式–高斯的密度函数)

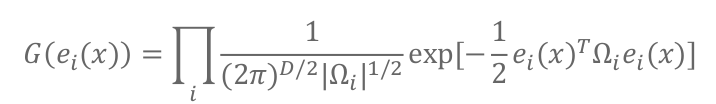
最终目标是使得误差尽可能趋近于0(均值)-----等价于每个高斯分布取得最大值,
就是上面那个公式的G(ei(x))取得最大值.(但是那个公司那么复杂,又是连乘和指数),要做一个变形,两边取ln,函数的单调性不变嘛,连乘则变为连加,成为下面形式:

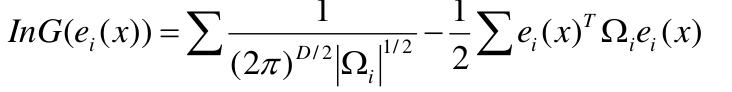
求lnG(ei(x))的最大值,那么前面的分数是和x没关系的可以去掉,就剩下-1/2和后面那部分,也就是后面那部分的最小值.
令非线性最小二乘的目标函数为:

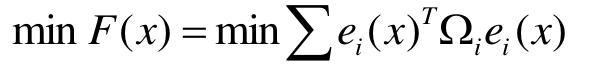
好了,现在得到了最终要求得目标函数

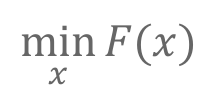
直接想法:求F(x)关于变量x的导数,令其等于0,求解方程即可。
对于凸函数来说,上述想法是可行的,但对于非凸函数(因为求完导还是非线性的),通常采用基于**梯度(本质就是把非线性函数线性化)**的优化方法。

非线性最小二乘问题的求解推导

那么下面就需要将F(x)线性化,用到的方法就是----泰勒展开

F(x)线性化:

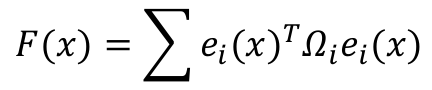
误差函数ei(x)是非线性函数,因此F(x)是关于x的非线性函数。
对误差函数ei(x)进行线性化,那么F(x)也就成了线性函数.对误差函数ei(x)进行线性化得到(泰勒展开的一阶近似公式):

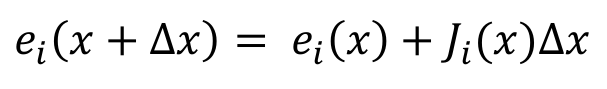
其中,J为映射函数F(x)对状态向量x的导数,称之为Jacobian(雅克比)矩阵。

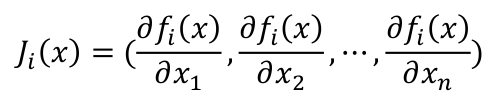
因此,函数F(x)的可化解为:

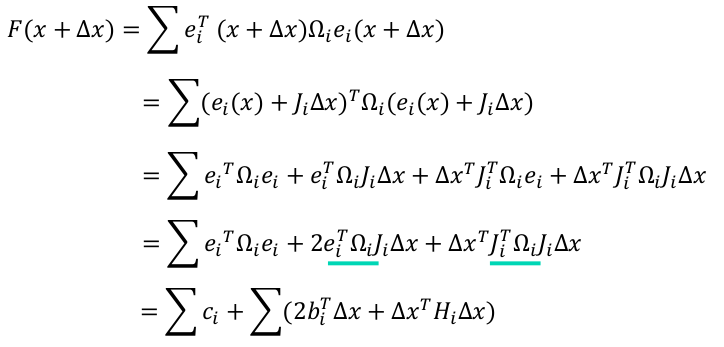
下面逐行解释上面的化解过程:

• 第一行到第二行就是把泰勒公式的一阶展开公式带入
• 第二行到第三行就是把括号里的相乘展开
• 第三行到第四行就是将中间的两项,合为一项,能合为一项的原因就是 两项都是一个数 ,然后互为转置,所有两项相等
• 第四行到第五行就是把复杂的和x每什么关系的用其它字母表示了
  
  然后继续,可以看到上面F(x + ∆x)化成的第五行形式,是关于变量∆x的二次函数,这个是个凸函数了
  要求F(x + ∆x)的最小值时,x的值,即令其关于∆x的导数等于0,此时即可得到∆x的值.为了更好的求∆x的偏导,我们继续化简F(x + ∆x)
  
  第一行变成第二行就是把连加的符合内与连加没有关系的项提了出来
  第二行变成第三行就是是把连加的部分有一个字母表示,只是看起来方便

到这里可以更方便的看出F(x + ∆x)是关于变量∆x的二次函数
求偏导得到:

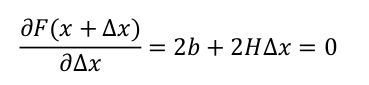
可以得到∆x为:

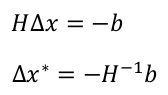
令x = x + ∆x∗ ,然后不断迭代,直至收敛即可。
这个∆x即为下降的梯度.

至此一个非线性最小二乘问题就得到了求解!

非线性最小二乘问题的求解方法总结

总结下上面的流程:
1 线性化误差函数:

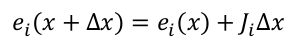
2 构建线性系统:

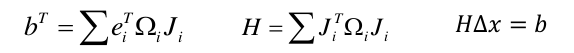
3 求解线性系统:

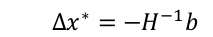
4 更新解,并不断迭代直至收敛:

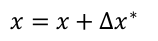
非线性最小二乘测试Code

上面理论上推导到非线性最小二乘的原理和解法.下面通过Code进行测试.

#include <iostream>
#include <opencv2/opencv.hpp>
#include <Eigen/Core>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main(int argc, char **argv) {
  double ar = 1.0, br = 2.0, cr = 1.0;         // 真实参数值
  double ae = 2.0, be = -1.0, ce = 5.0;        // 估计参数值
  int N = 100;                                 // 数据点
  double w_sigma = 1.0;                        // 噪声Sigma值
  double inv_sigma = 1.0 / w_sigma;
  cv::RNG rng;   
                                // OpenCV随机数产生器
  vector<double> x_data, y_data;      // 数据
  for (int i = 0; i < N; i++) {
    double x = i / 100.0;
    x_data.push_back(x);
    y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
  }
  
  // 开始Gauss-Newton迭代
  int iterations = 100;    // 迭代次数
  double cost = 0, lastCost = 0;  // 本次迭代的cost和上一次迭代的cost
  
  for (int iter = 0; iter < iterations; iter++) {
    Matrix3d H = Matrix3d::Zero();             // Hessian = J^T W^{-1} J in Gauss-Newton
    Vector3d b = Vector3d::Zero();             // bias
    cost = 0;
    for (int i = 0; i < N; i++) {
      double xi = x_data[i], yi = y_data[i];  // 第i个数据点
      double error = yi - exp(ae * xi * xi + be * xi + ce);
      Vector3d J; // 雅可比矩阵
      J[0] = -xi * xi * exp(ae * xi * xi + be * xi + ce);  // de/da
      J[1] = -xi * exp(ae * xi * xi + be * xi + ce);  // de/db
      J[2] = -exp(ae * xi * xi + be * xi + ce);  // de/dc
      H += inv_sigma * inv_sigma * J * J.transpose();
      b += -inv_sigma * inv_sigma * error * J;
      cost += error * error;
    }
 
    // 求解线性方程 Hx=b
    Vector3d dx = H.ldlt().solve(b);
    if (isnan(dx[0])) {
      cout << "result is nan!" << endl;
      break;
    }
    if (iter > 0 && cost >= lastCost) {
      cout << "cost: " << cost << ">= last cost: " << lastCost << ", break." << endl;
      break;
    }
    ae += dx[0];
    be += dx[1];
    ce += dx[2];
    lastCost = cost;
    cout << "total cost: " << cost << ", \t\tupdate: " << dx.transpose() <<
         "\t\testimated params: " << ae << "," << be << "," << ce << endl;
  }
  cout << "estimated abc = " << ae << ", " << be << ", " << ce << endl;
  return 0;
}

文章来源: blog.csdn.net，作者：月照银海似蛟龙，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/qq_32761549/article/details/123429398