激光SLAM:图优化--使用开源库G2O对之前例子进行优化
首先进行G2O的简介
G2O简介
G2O(General Graphic Optimization)
在SLAM领域,基于图优化的一个用的非常广泛的库就是g2o,是一个用来优化非线性误差函数的c++框架.
G2O是一个重度模板类的c++项目,所以一定要先了解清楚其框架,才能知道如何使用.
G2O框架

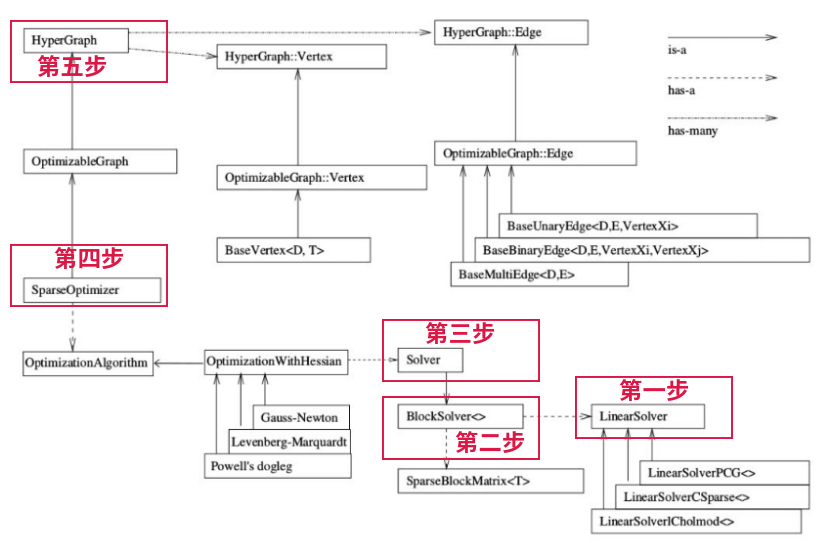
这个图很重要,决定了它如何使用.
- SparseOptimizer是整个图的核心,找到它向上走,它是一个Optimizable Graph 也就是一个超图HyperGraph,所以在使用时需要添加顶点和边.
- 顶点(HyperGraph::Vertex)和边(HyperGraph::Edge),顶点继承自 Base Vertex,边可以继承自BaseUnaryEdge(单边), BaseBinaryEdge(双边)或BaseMultiEdge(多边)
- 整个框架的上部分就说的顶点和边(图的结构),下部分就是优化算法.SparseOptimizer包含一个优化算法OptimizationAlgorithm的对象,通过OptimizationWithHessian 来实现的.迭代策略可以从Gauss-Newton(高斯牛顿法,简称GN), Levernberg-Marquardt(简称LM法), Powell’s dogleg 三者中间选择一个
- OptimizationWithHessian 内部包含一个求解器Solver,Solver实际是由一个BlockSolver组成的.
- BlockSolver有两个部分,一个是SparseBlockMatrix ,用于计算稀疏的雅可比和Hessian矩阵;一个是线性方程的求解器LinearSolver,它用于计算迭代过程中最关键的一步HΔx=−b,LinearSolver有几种方法可以选择:PCG, CSparse, Choldmod
G2O通用使用流程
由于在使用的过程,c++模板的时候需要用下层的模块初始化,所以在使用的时候需要从下向上的构建.如下图标出了5个步骤,及顺序.
- 创建一个线性求解器LinearSolver
- 创建BlockSolver。并用上面定义的线性求解器初始化
- 创建总求解器solver。并从GN, LM, DogLeg 中选一个,再用上述块求解器BlockSolver初始化
- 创建SparseOptimizer 稀疏优化器
- 定义图的顶点和边。并添加到SparseOptimizer中
- 设置优化参数,开始执行优化
下面再详细的介绍下各个步骤
第一步:
创建一个线性求解器LinearSolver
根据前面的博客知道,增量方程的形式是:H△X=-b,并且已知H矩阵是一个稀疏矩阵,G2O在内部实现了求解稀疏矩阵的方法

在图上的路径下存在着这五个文件夹,就是求解稀疏矩阵的线性方法方法.这里总结下这五个方法:
- Cholmod :使用sparse cholesky分解法。继承自LinearSolverCCS
- CSparse:使用CSparse法。继承自LinearSolverCCS
- PCG :使用preconditioned conjugate gradient 法,继承自LinearSolver
- Dense :使用dense cholesky分解法。继承自LinearSolver
- Eigen: 依赖项只有eigen,使用eigen中sparse Cholesky 求解,继承自LinearSolver
在代码中如何设置呢?
打开一个方法的h文件,看它的类的名称即可.例如Cholmod

就实例化一个这个类,赋值给LinearSolverType即可.
e.g.
Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>();
Block::LinearSolverType* linearSolver = new g2o::LinearSolverEigen<Block::PoseMatrixType>();
Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse<Block::PoseMatrixType>();
- 1
- 2
- 3
第二步:
创建BlockSolver。并用上面定义的线性求解器初始化
由于BlockSolver 内部包含 LinearSolver,所以需要用上面我们定义的线性求解器LinearSolver来初始化。
其定义的文件在g2o/g2o/core/block_solver.h
再定义block的时候可以设置维度,

其中p代表pose的维度,l表示landmark的维度
有一些常用的维度类型,在h文件里也做了定义:

当然也有可变尺寸的solver,因为在某些应用场景Pose和Landmark在程序开始时并不能确定.

在用g2o写代码的时候,已知维度的话,一般我们用 typedef 先将BlockSolver设定下,例如下面
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 3>> Block; // 每个误差项优化变量维度为3,误差值维度为3
- 1
这个就是我们之前博客里写的例子,pose是3维的,误差向量也是3维的.
然后创建 BlockSolver(用第一步创建的linearSolver初始化),如下:
Block* solver_ptr = new Block(linearSolver);
- 1
至此第二步就完成了.
第三步:
创建总求解器solver。并从GN, LM, DogLeg 中选一个,再用第二步创建的块求解器BlockSolver初始化
现在阶段,可以选择的方法有三种:

用第二步创建的块求解器BlockSolver初始化,代码写成如下形式:
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
- 1
- 2
- 3
选其中一个就行
第4步:
创建终稀疏优化器SparseOptimizer,并用第三步创建的求解器solver设置为求解方法。
代码如下:
创建稀疏优化器
g2o::SparseOptimizer optimizer;
- 1
用第三步创建的求解器solver设置为求解方法
optimizer.setAlgorithm(solver);
- 1
第五步:
定义图的顶点和边。并添加到SparseOptimizer中。
在添加顶点的时候需要知道自己的定点类型,看g2o里面是否已有,如果有的话则不需要自己再定义了.这里把g2o已定义好的罗列下
VertexSE2 : public BaseVertex<3, SE2> //2D pose Vertex, (x,y,theta)
VertexSE3 : public BaseVertex<6, Isometry3> //6d vector (x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion)
VertexPointXY : public BaseVertex<2, Vector2>
VertexPointXYZ : public BaseVertex<3, Vector3>
VertexSBAPointXYZ : public BaseVertex<3, Vector3>
// SE3 Vertex parameterized internally with a transformation matrix and externally with its exponential map
VertexSE3Expmap : public BaseVertex<6, SE3Quat>
// SBACam Vertex, (x,y,z,qw,qx,qy,qz),(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion.
// qw is assumed to be positive, otherwise there is an ambiguity in qx,qy,qz as a rotation
VertexCam : public BaseVertex<6, SBACam>
// Sim3 Vertex, (x,y,z,qw,qx,qy,qz),7d vector,(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion.
VertexSim3Expmap : public BaseVertex<7, Sim3>
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
很明显对于我们之前博客的顶点类型应该选择VertexSE2
其中SE2是李群的概念,对于二维的 x y θ 组成的变换矩阵T(R,t)属于SE2
对于三维的 x y z pitch roll yaw 组成的变换矩阵T(R,t)属于SE3,注意应该使用VertexSE3Expmap的类型而不是VertexSE3
for (size_t i = 0; i < Vertexs.size(); i++) {
VertexSE2* v = new VertexSE2();
v->setEstimate(Vertexs[i]);
v->setId(i);
if (i == 0) {
v->setFixed(true);
}
optimizer.addVertex(v);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
同样的边的类型应该选择 EdgeSE2
for (size_t i = 0; i < Edges.size(); i++) {
EdgeSE2* edge = new EdgeSE2();
Edge tmpEdge = Edges[i];
edge->setId(i);
edge->setVertex(0, optimizer.vertices()[tmpEdge.xi]);
edge->setVertex(1, optimizer.vertices()[tmpEdge.xj]);
edge->setMeasurement(tmpEdge.measurement);
edge->setInformation(tmpEdge.infoMatrix);
optimizer.addEdge(edge);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
第六步:
设置优化参数,开始执行优化。
必须设置的有
- SparseOptimizer的初始化
optimizer.initializeOptimization();
- 1
- SparseOptimizer的迭代次数,此行代码就可以执行优化了
optimizer.optimize(100);
- 1
ok了,已经可以用g2o进行之前例子的优化了.
下面给出代码
Code
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 3>> Block; // 每个误差项优化变量维度为3,误差值维度为3
/*创建线性求解器*/
// Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>();
// Block::LinearSolverType* linearSolver = new g2o::LinearSolverEigen<Block::PoseMatrixType>();
Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse<Block::PoseMatrixType>();
/*创建BlockSolver*/
Block* solver_ptr = new Block(linearSolver);
/*创建总求解器solver。并从GN, LM, DogLeg 中选一个*/
// g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
// g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
/*创建SparseOptimizer 稀疏优化器*/
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm(solver);
/*添加顶点*/
for (size_t i = 0; i < Vertexs.size(); i++) {
VertexSE2* v = new VertexSE2();
v->setEstimate(Vertexs[i]);
v->setId(i);
if (i == 0) {
v->setFixed(true);
}
optimizer.addVertex(v);
}
/*添加边*/
for (size_t i = 0; i < Edges.size(); i++) {
EdgeSE2* edge = new EdgeSE2();
Edge tmpEdge = Edges[i];
edge->setId(i);
edge->setVertex(0, optimizer.vertices()[tmpEdge.xi]);
edge->setVertex(1, optimizer.vertices()[tmpEdge.xj]);
edge->setMeasurement(tmpEdge.measurement);
edge->setInformation(tmpEdge.infoMatrix);
optimizer.addEdge(edge);
}
/*设置优化参数 并求解*/
optimizer.setVerbose(true);
optimizer.initializeOptimization();
SparseOptimizerTerminateAction* terminateAction = new SparseOptimizerTerminateAction;
terminateAction->setGainThreshold(1e-4);
optimizer.addPostIterationAction(terminateAction);
optimizer.optimize(100);
/*取出求解结果*/
for (size_t i = 0; i < Vertexs.size(); i++) {
VertexSE2* v = static_cast<VertexSE2*>(optimizer.vertices()[i]);
Vertexs[i] = v->estimate().toVector();
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
同样在前后加入在rviz里显示位姿的代码,查看其优化结果
Resul
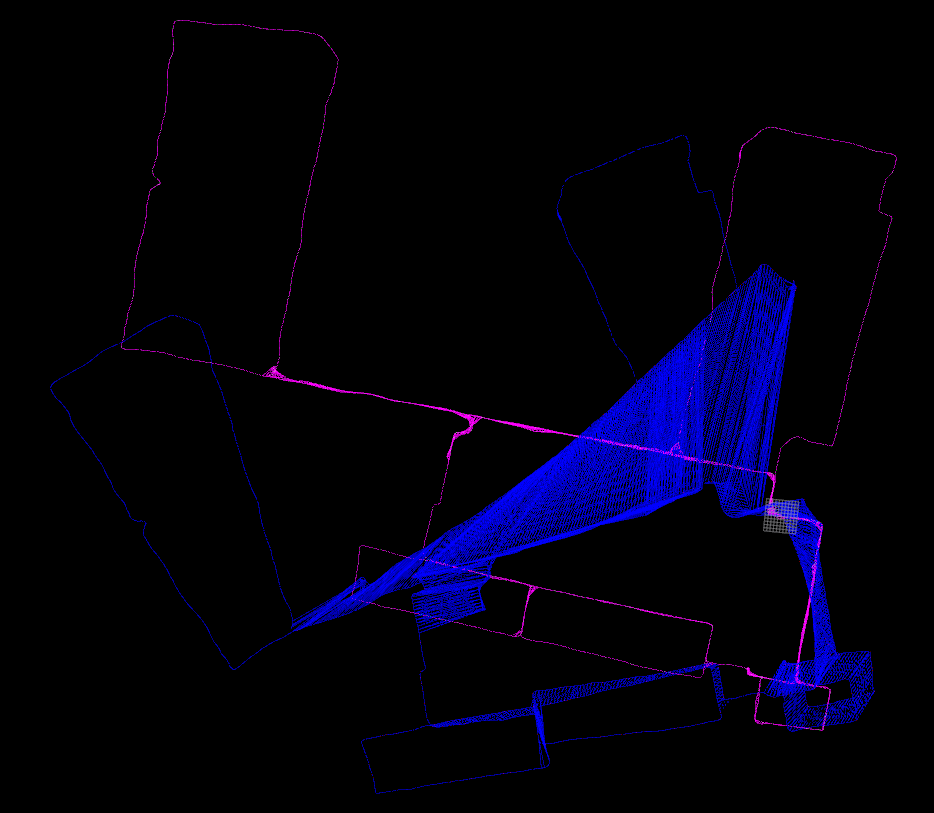
蓝色的是优化前的位姿图,粉色是优化后的位姿图.
文章来源: blog.csdn.net,作者:月照银海似蛟龙,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/qq_32761549/article/details/123652227
- 点赞
- 收藏
- 关注作者



评论(0)