Java工程师丨面试真题（二）
【摘要】 一、附加题描述二阶魔方又叫小魔方，是2*2*2的立方形结构。每一面都有4个块，共有24个块。每次操作可以将任意一面逆时针或者顺时针旋转90°，如将上面逆时针旋转90°操作如下。编辑Nero在小魔方上做了一些改动，用数字替换每个块上面的颜色，称之为数字魔方。魔方上每一面的优美度就是这个面上4个数字的乘积，而魔方的总优美度就是6个面优美度总和。现在Nero有一个数字魔方，他想知道这个魔方...
一、附加题
描述
二阶魔方又叫小魔方，是2*2*2的立方形结构。每一面都有4个块，共有24个块。每次操作可以将任意一面逆时针或者顺时针旋转90°，如将上面逆时针旋转90°操作如下。
Nero在小魔方上做了一些改动，用数字替换每个块上面的颜色，称之为数字魔方。魔方上每一面的优美度就是这个面上4个数字的乘积，而魔方的总优美度就是6个面优美度总和。
现在Nero有一个数字魔方，他想知道这个魔方在操作不超过5次的前提下能达到的最大优美度是多少。
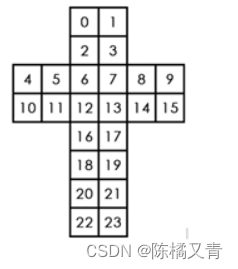
魔方展开后每一块的序号如下图：
输入描述：
输入一行包含24个数字，按序号顺序给出魔方每一块上面的数字。所有数大小范围为[-100,100]。
输出描述：
输出一行包含一个数字，表示最大优美度。
示例1
输入：
2 -3 -2 3 7 -6 -6 -7 9 -5 -9 -3 -2 1 4 -9 -1 -10 -5 -5 -10 -4 8 2输出：
8281
题解：
import java.util.*;
public class Main {
/**
* 记录三种旋转需要变动的下标，共三组下标
* 每组下标里，每4个下标形成一个轮回
*/
private static int[][] map = new int[][]{
{0,1,3,2,7,5,22,9,6,4,23,8},
{6,7,13,12,2,8,17,11,3,14,16,5},
{4,5,11,10,0,6,16,20,2,12,18,22}
};
/**
* main
* @param args 命令行参数
*/
public static void main(String[] args) {
// 读取输入
Scanner sc = new Scanner(System.in);
int[] n = new int[24];
for (int i = 0; i < 24; i++) {
n[i] = sc.nextInt();
}
// 输出结果
System.out.println(resolve(n, -1, 5));
}
/**
* 分析当前状态
* @param n 当前状态
* @param type 达到当前状态时的最后一个操作类型
* @param remain 剩余操作数
* @return 可以达到的最大优美度
*/
private static int resolve(int[] n, int type, int remain) {
// 非法状态
if (remain < 0) return Integer.MIN_VALUE;
// 当前状态优美度
int max = compute(n);
// 尝试转动，不可与type类型相同
if (type != 0) max = Math.max(max, turn(n, 0, remain));
if (type != 1) max = Math.max(max, turn(n, 1, remain));
if (type != 2) max = Math.max(max, turn(n, 2, remain));
return max;
}
/**
* 按照类型转动魔方多次并分析
* @param n 当前状态
* @param type 转动类型
* @param remain 剩余操作数
* @return 转动可以达到的最大优美度
*/
private static int turn(int[] n, int type, int remain) {
// 转动一次
turn(n, type);
int max = resolve(n, type, remain-1);
// 转动两次
turn(n, type);
max = Math.max(max, resolve(n, type, remain-2));
// 转动三次，相当于逆向转动一次
turn(n, type);
max = Math.max(max, resolve(n, type, remain-1));
// 转动四次，还原初始状态
turn(n, type);
return max;
}
/**
* 转动操作
* @param n 当前状态
* @param type 转动类型
*/
private static void turn(int[] n, int type) {
// 每四个下标一轮回
for (int i = 0, tmp = 0; i < 12; i++) {
if (i % 4 == 0) tmp = n[map[type][i]];
if (i % 4 == 3) n[map[type][i]] = tmp;
else n[map[type][i]] = n[map[type][i+1]];
}
}
/**
* 计算当前状态的优美度
* @param n 当前状态
* @return 优美度
*/
private static int compute(int[] n) {
return n[0]*n[1]*n[2]*n[3] +
n[6]*n[7]*n[12]*n[13] +
n[4]*n[5]*n[10]*n[11] +
n[8]*n[9]*n[14]*n[15] +
n[16]*n[17]*n[18]*n[19] +
n[20]*n[21]*n[22]*n[23];
}
}二、编程题1
描述
有一个推箱子的游戏, 一开始的情况如下图:
上图中, '.' 表示可到达的位置, '#' 表示不可到达的位置，其中 S 表示你起始的位置, 0表示初始箱子的位置, E表示预期箱子的位置，你可以走到箱子的上下左右任意一侧, 将箱子向另一侧推动。如下图将箱子向右推动一格;
..S0.. -> ...S0.
注意不能将箱子推动到'#'上, 也不能将箱子推出边界;
现在, 给你游戏的初始样子, 你需要输出最少几步能够完成游戏, 如果不能完成, 则输出-1。
输入描述：
第一行为2个数字,n, m, 表示游戏盘面大小有n 行m 列(5< n, m < 50);
后面为n行字符串,每行字符串有m字符, 表示游戏盘面;
输出描述：
一个数字,表示最少几步能完成游戏,如果不能,输出-1;
示例1
输入：
3 6 .S#..E .#.0.. ......输出：
11
题解：
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class Main {
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int m=sc.nextInt();
char[][] chas=new char[n][m];
// 人的起始位置S 以及箱子的位置
int startX=0,startY=0,boxX=0,boxY=0;
// 判断位置 ，即人要先找到箱子，再推着箱子往前走
for(int i=0;i&lt;n;i++){
String string=sc.next();
for(int j=0;j&lt;m;j++){
chas[i][j]=string.charAt(j);
if(chas[i][j]==&#39;S&#39;){
startX=i;
startY=j;
}
if(chas[i][j]==&#39;0&#39;){
boxX=i;
boxY=j;
}
}
}
System.out.println(solve(chas,startX,startY,boxX,boxY));
}
public static class Node{
int px; // 人的位置
int py;
int bx; //箱子的位置
int by;
int step; //从初始位置到现在节点所走的步数
public Node(int px,int py,int bx,int by){
this.px=px;
this.py=py;
this.bx=bx;
this.by=by;
}
}
private static int solve(char[][] chas,int startX, int startY,int boxX,int boxY) {
Node start=new Node(startX, startY,boxX,boxY);
int n=chas.length;
int m=chas[0].length;
// iswalked四维数组，可以用来存储走过的路径以防重复。
int[][][][] iswalked=new int[n][m][n][m];
// 每个节点都有dir4个方向的移动，分别是 下右上左
int[][] movedir=new int[][]{{1,0},{0,1},{-1,0},{0,-1}};
Queue&lt;Node&gt; que=new LinkedList&lt;&gt;(); //利用队列实现BFS
start.step=0;
que.add(start);
//开始BFS广度搜索最短路径
while(!que.isEmpty()){
Node cur=que.poll();
int newBx=cur.bx;
int newBy=cur.by;
for(int i=0;i&lt;4;i++){ // 向4个方向走
//人在箱子左边或右边
if(cur.px==cur.bx){
if (cur.py+movedir[i][1]==cur.by){
newBy = cur.by+movedir[i][1];
}else{
newBy = cur.by;
}
}
//人在箱子上面或下面
if(cur.py==cur.by){
if(cur.px+movedir[i][0]==cur.bx){
newBx = cur.bx+movedir[i][0];
}else{
newBx = cur.bx;
}
}
// 箱子找到了要随人往4个方向动；没找到则箱子不动人动
Node next=new Node(cur.px+movedir[i][0], cur.py+movedir[i][1],newBx,newBy);
//不能让人在没找到箱子之前出地图或者自己提前到目的地
if(next.px&lt;0||next.px&gt;=n||next.py&lt;0||next.py&gt;=m||chas[next.px][next.py]==&#39;#&#39;
||next.bx&lt;0||next.bx&gt;=n||next.by&lt;0||next.by&gt;=m
||chas[next.bx][next.by]==&#39;#&#39;){
continue;
}
// 0说明这条路径没有走过
if(iswalked[next.px][next.py][next.bx][next.by]==0){
iswalked[next.px][next.py][next.bx][next.by]=1;
next.step=cur.step+1;
if(chas[next.bx][next.by]==&#39;E&#39;){ //此时把箱子推到终点了
return next.step; // 最先到终点的就是最短路径
}
que.add(next);
}
}
}
return -1;
}
}三、编程题2
描述
有n个房间，现在i号房间里的人需要被重新分配，分配的规则是这样的：先让i号房间里的人全都出来，接下来按照 i+1, i+2, i+3, ... 的顺序依此往这些房间里放一个人，n号房间的的下一个房间是1号房间，直到所有的人都被重新分配。
现在告诉你分配完后每个房间的人数以及最后一个人被分配的房间号x，你需要求出分配前每个房间的人数。数据保证一定有解，若有多解输出任意一个解。
输入描述：
第一行两个整数n, x (2<=n<=10^5, 1<=x<=n)，代表房间房间数量以及最后一个人被分配的房间号；
第二行n个整数 a_i(0<=a_i<=10^9) ，代表每个房间分配后的人数。
输出描述：
输出n个整数，代表每个房间分配前的人数。
示例1
输入：
3 1 6 5 1输出：
4 4 4
题解：
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int x = scanner.nextInt() - 1;
long[] room = new long[n];
long min = Long.MAX_VALUE;
for (int i = 0; i < n; i++) {
room[i] = scanner.nextInt();
if (room[i] < min)
min = room[i];
}
//get min_index
int minIndex = x;
while (room[minIndex] != min) {
minIndex = minIndex > 0 ? minIndex - 1 : n - 1;
}
// remove the round number.
for (int i = 0; i < n; i++) {
room[i] -= min;
}
// remove the tail
int remain = 0;
for (int i = x; i != minIndex; i = i > 0 ? i - 1 : n - 1) {
room[i] -= 1;
remain += 1;
}
room[minIndex] += remain + n * min;
//print the result
for (int i = 0; i < n; i++) {
System.out.print(room[i] + " ");
}
}
}四、字母交换
描述
【编码题】字符串S由小写字母构成，长度为n。定义一种操作，每次都可以挑选字符串中任意的两个相邻字母进行交换。询问在至多交换m次之后，字符串中最多有多少个连续的位置上的字母相同？
输入描述：
第一行为一个字符串S与一个非负整数m。(1 <= |S| <= 1000, 1 <= m <= 1000000)
输出描述：
一个非负整数，表示操作之后，连续最长的相同字母数量。
示例1
输入：
abcbaa 2输出：
2说明：
使2个字母a连续出现，至少需要3次操作。即把第1个位置上的a移动到第4个位置。 所以在至多操作2次的情况下，最多只能使2个b或2个a连续出现。
题解：
import java.util.*;
public class Main{
static int res = 1;
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
String input = scanner.nextLine();
String str = input.split(" ")[0];
int m = Integer.parseInt(input.split(" ")[1]);
HashMap<Character, List<Integer>> map = new HashMap<>();
char[] chars = str.toCharArray();
int len = chars.length;
for(int i = 0; i < len; i++){
List<Integer> list = map.getOrDefault(chars[i], new ArrayList<>());
list.add(i);
map.put(chars[i], list);
}
for(int i = 0; i < len; i++){
char c = chars[i];
List<Integer> list = map.get(c);
moveTogether(list, i, m);
/*
int lessCount = 0;
for(int num : list){
if(num < i){
lessCount++;
}
else{
break;
}
}
int greatCount = list.size()-1-lessCount;
for(int j = 0; j < lessCount; i++){
int cur = list.get(j);
// 现在这个节点的位置在cur,要移动到 （0 1 j 3 4 ... lessCount-1）i
// lesscount-2的时候对应i-2
// lesscount-1的时候对应i-1
int target = i + j - lessCount;
int times =
}
}
*/
}
System.out.println(res);
}
// 在times步内，尽可能把list里面的数字移动到mid周围
public static void moveTogether(List<Integer> list, int mid, int times){
int len = list.size();
int mid_index = 0;
for(int i = 0; i < len; i++){
if(list.get(i) == mid){
mid_index = i;
break;
}
}
int left_index = mid_index-1;
int right_index = mid_index+1;
int count = 1;
// mid为中心的左右边界
int left_mid = mid-1;
int right_mid = mid+1;
while(times > 0){
if(left_index < 0 && right_index >= len){
break;
}
// 看一下左边和右边哪个更近一点
int left_dist;
if(left_index < 0)
left_dist = Integer.MAX_VALUE / 2;
else
left_dist = left_mid - list.get(left_index);
int right_dist;
if(right_index >= len) {
right_dist = Integer.MAX_VALUE / 2;
}
else {
right_dist = list.get(right_index) - right_mid;
}
if(left_dist > right_dist){
// 右边靠更加近一点
if(times < right_dist) break;
times -= right_dist;
right_mid++;
count++;
right_index++;
}
else{
if(times < left_dist) break;
times -= left_dist;
left_mid--;
left_index--;
count++;
}
}
res = Math.max(count, res);
}
}
【声明】本内容来自华为云开发者社区博主，不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源（华为云社区）、文章链接、文章作者等基本信息，否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）