蓝桥杯第十五讲--复杂dp【例题】
前言
蓝桥杯官网:蓝桥杯大赛——全国大学生TMT行业赛事
✨本博客讲解 蓝桥杯C/C++ 备赛所涉及算法知识,此博客为第十五讲:复杂dp【例题】
本篇博客所包含习题有:
👊鸣人的影分身
👊糖果
👊密码脱落
👊生命之树
复杂dp【习题】见博客:蓝桥杯第十五讲–复杂dp【习题】
如果你觉得本章节有些难度,建议先修如下两篇博客:
蓝桥杯第六讲–简单dp【例题】
蓝桥杯第六讲–简单dp【习题】
博客内容以题代讲,通过讲解题目的做法来帮助读者快速理解算法内容,需要注意:学习算法不能光过脑,更要实践,请读者务必自己敲写一遍本博客相关代码!!!
鸣人的影分身
题目要求
题目描述:
在火影忍者的世界里,令敌人捉摸不透是非常关键的。
我们的主角漩涡鸣人所拥有的一个招数——多重影分身之术——就是一个很好的例子。
影分身是由鸣人身体的查克拉能量制造的,使用的查克拉越多,制造出的影分身越强。
针对不同的作战情况,鸣人可以选择制造出各种强度的影分身,有的用来佯攻,有的用来发起致命一击。
那么问题来了,假设鸣人的查克拉能量为 M M M,他影分身的个数最多为 N N N,那么制造影分身时有多少种不同的分配方法?
注意:
- 影分身可以分配 0 0 0 点能量。
- 分配方案不考虑顺序,例如: M = 7 , N = 3 M=7,N=3 M=7,N=3,那么 ( 2 , 2 , 3 ) (2,2,3) (2,2,3) 和 ( 2 , 3 , 2 ) (2,3,2) (2,3,2) 被视为同一种方案。
输入格式:
第一行是测试数据的数目 t t t。
以下每行均包含二个整数 M M M 和 N N N,以空格分开。
输出格式:
对输入的每组数据 M M M 和 N N N,用一行输出分配的方法数。
数据范围:
0 ≤ t ≤ 20 , 0≤t≤20 , 0≤t≤20,
1 ≤ M , N ≤ 10 1≤M,N≤10 1≤M,N≤10
输入样例:
1
7 3
- 1
- 2
输出样例:
8
- 1
思路分析
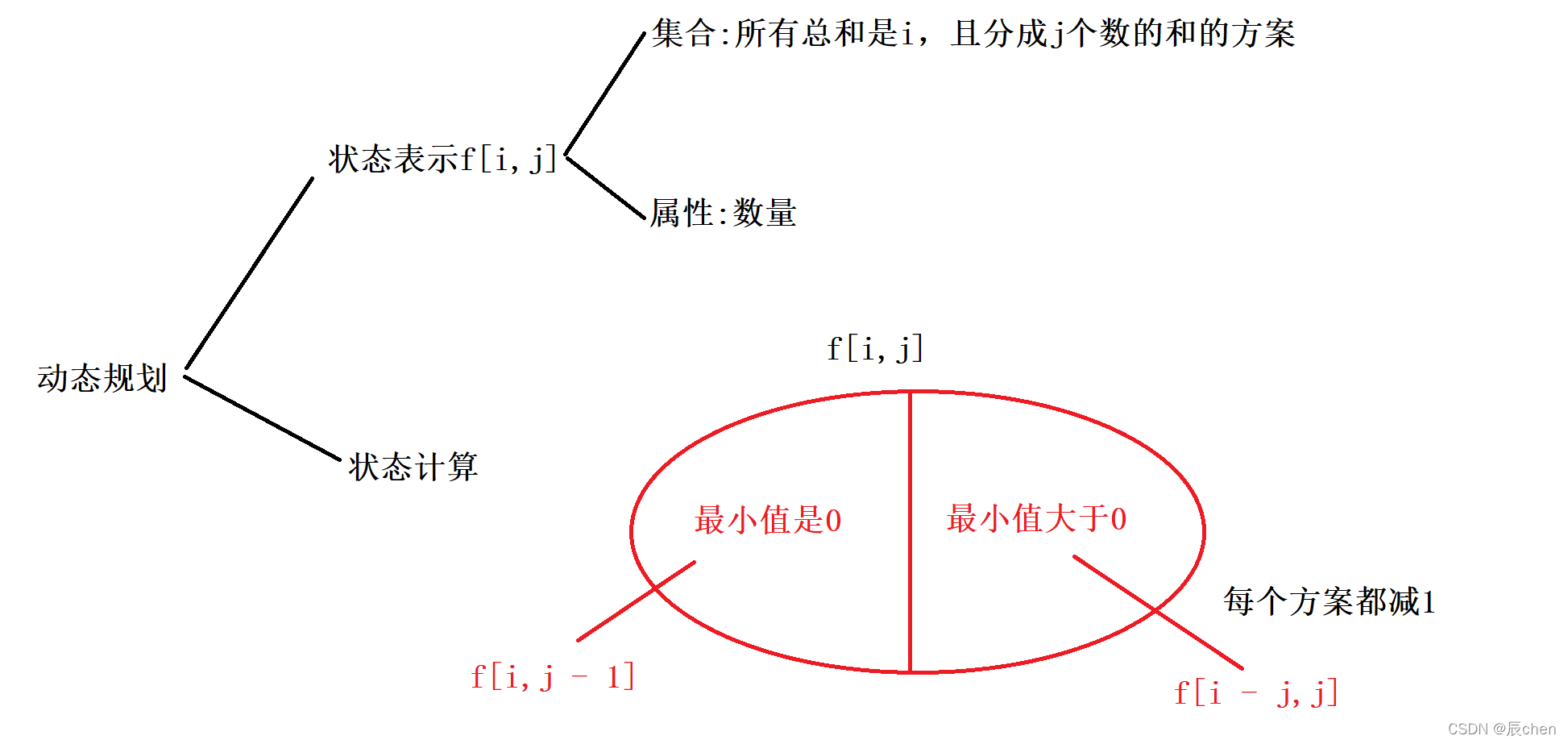
代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 11;
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
int n, m;
scanf("%d%d", &m, &n);
int f[N][N] = {0};
f[0][0] = 1;
for (int i = 0; i <= m; i ++ )
for (int j = 1; j <= n; j ++ )
{
f[i][j] = f[i][j - 1];
if (i >= j) f[i][j] += f[i - j][j];
}
printf("%d\n", f[m][n]);
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
糖果
题目要求
题目描述:
由于在维护世界和平的事务中做出巨大贡献, D z x Dzx Dzx 被赠予糖果公司 2010 2010 2010 年 5 5 5 月 23 23 23 日当天无限量糖果免费优惠券。
在这一天, D z x Dzx Dzx 可以从糖果公司的 N N N 件产品中任意选择若干件带回家享用。
糖果公司的 N N N 件产品每件都包含数量不同的糖果。
D z x Dzx Dzx 希望他选择的产品包含的糖果总数是 K K K 的整数倍,这样他才能平均地将糖果分给帮助他维护世界和平的伙伴们。
当然,在满足这一条件的基础上,糖果总数越多越好。
D z x Dzx Dzx 最多能带走多少糖果呢?
注意: D z x Dzx Dzx 只能将糖果公司的产品整件带走。
输入格式:
第一行包含两个整数 N N N 和 K K K。
以下 N N N 行每行 1 1 1 个整数,表示糖果公司该件产品中包含的糖果数目,不超过 1000000 1000000 1000000。
输出格式:
符合要求的最多能达到的糖果总数,如果不能达到 K K K 的倍数这一要求,输出 0 0 0。
数据范围:
1 ≤ N ≤ 100 , 1≤N≤100, 1≤N≤100,
1 ≤ K ≤ 100 , 1≤K≤100, 1≤K≤100,
输入样例:
5 7
1
2
3
4
5
- 1
- 2
- 3
- 4
- 5
- 6
输出样例:
14
- 1
样例解释:
D z x Dzx Dzx 的选择是 2 + 3 + 4 + 5 = 14 2+3+4+5=14 2+3+4+5=14,这样糖果总数是 7 7 7 的倍数,并且是总数最多的选择。
思路分析
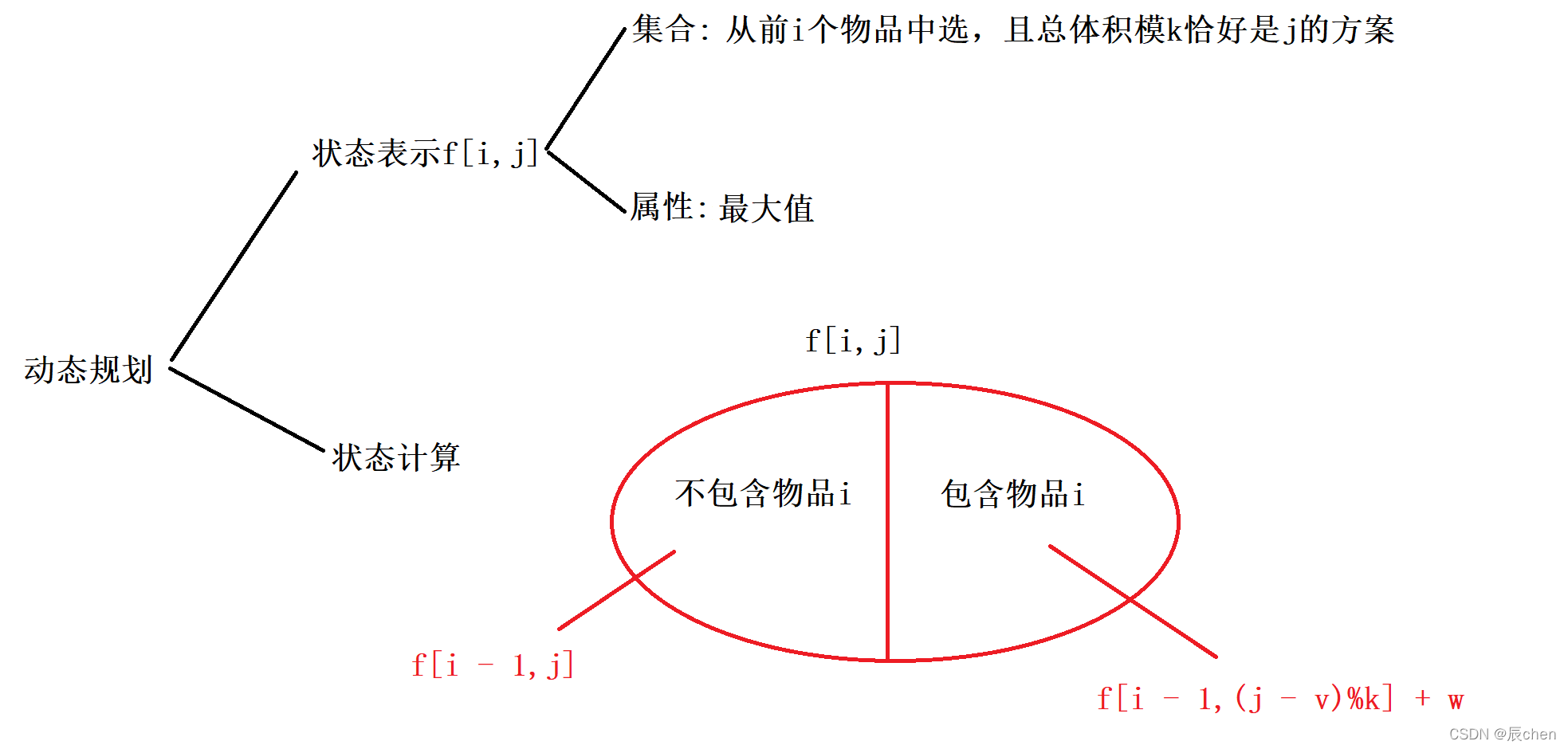
代码
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 110;
int n, k;
int f[N][N];
int max(int x, int y)
{
return x > y ? x : y;
}
int main()
{
scanf("%d%d", &n, &k);
memset(f, -0x3f, sizeof f);
f[0][0] = 0;
for (int i = 1; i <= n; i ++ )
{
int w;
scanf("%d", &w);
for (int j = 0; j < k; j ++ )
f[i][j] = max(f[i - 1][j], f[i - 1][(j + k - w % k) % k] + w);
}
printf("%d\n", f[n][0]);
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
密码脱落
来源: 第七届蓝桥杯省赛C++A/C组,第七届蓝桥杯省赛JAVAC组
题目要求
题目描述:
X X X 星球的考古学家发现了一批古代留下来的密码。
这些密码是由 A 、 B 、 C 、 D A、B、C、D A、B、C、D 四种植物的种子串成的序列。
仔细分析发现,这些密码串当初应该是前后对称的(也就是我们说的镜像串)。
由于年代久远,其中许多种子脱落了,因而可能会失去镜像的特征。
你的任务是:
给定一个现在看到的密码串,计算一下从当初的状态,它要至少脱落多少个种子,才可能会变成现在的样子。
输入格式:
共一行,包含一个由大写字母 A B C D ABCD ABCD 构成的字符串,表示现在看到的密码串。
输出格式:
输出一个整数,表示至少脱落了多少个种子。
数据范围:
输入字符串长度不超过 1000 1000 1000
输入样例1:
ABCBA
- 1
输出样例1:
0
- 1
输入样例2:
ABDCDCBABC
- 1
输出样例2:
3
- 1
思路分析
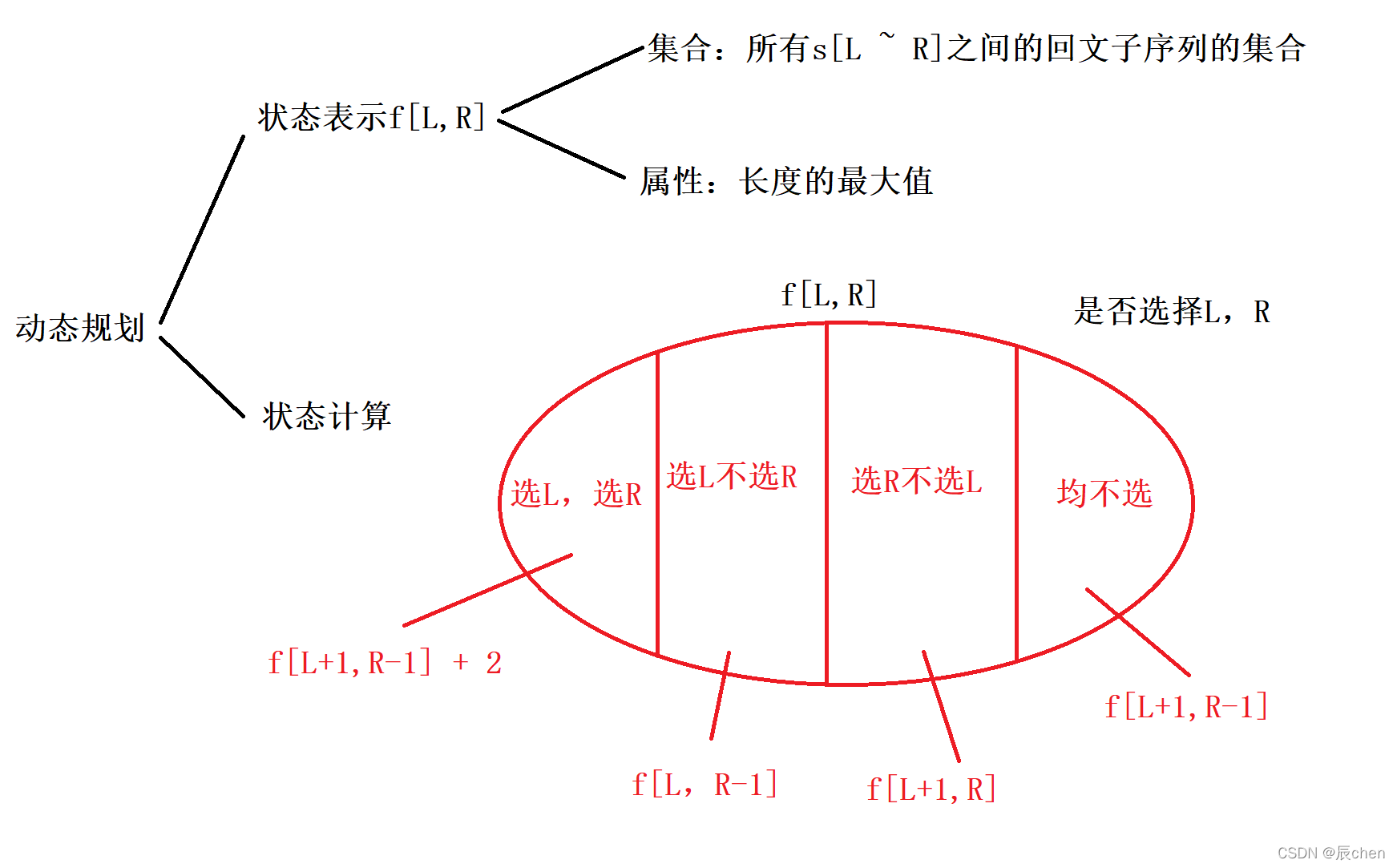
代码
#include <cstdio>
#include <string.h>
const int N = 1010;
char s[N];
int f[N][N];
int main()
{
scanf("%s", s);
int n = strlen(s);
for (int len = 1; len <= n; len ++ )
for (int l = 0; l + len - 1 < n; l ++ )
{
int r = l + len - 1;
if (len == 1) f[l][r] = 1;
else
{
if (s[l] == s[r]) f[l][r] = f[l + 1][r - 1] + 2;
if (f[l][r - 1] > f[l][r]) f[l][r] = f[l][r - 1];
if (f[l + 1][r] > f[l][r]) f[l][r] = f[l + 1][r];
}
}
printf("%d\n", n - f[0][n - 1]);
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
生命之树
来源: 第六届蓝桥杯省赛C++B组,第六届蓝桥杯省赛JAVAB组
题目要求
题目描述:
在 X X X 森林里,上帝创建了生命之树。
他给每棵树的每个节点(叶子也称为一个节点)上,都标了一个整数,代表这个点的和谐值。
上帝要在这棵树内选出一个非空节点集 S S S,使得对于 S S S 中的任意两个点 a , b a,b a,b,都存在一个点列 { a , v 1 , v 2 , … , v k , b } \{a,v1,v2,…,vk,b\} {a,v1,v2,…,vk,b} 使得这个点列中的每个点都是 S S S 里面的元素,且序列中相邻两个点间有一条边相连。
在这个前提下,上帝要使得 S S S 中的点所对应的整数的和尽量大。
这个最大的和就是上帝给生命之树的评分。
经过 a t m atm atm 的努力,他已经知道了上帝给每棵树上每个节点上的整数。
但是由于 a t m atm atm 不擅长计算,他不知道怎样有效的求评分。
他需要你为他写一个程序来计算一棵树的分数。
输入格式:
第一行一个整数 n n n 表示这棵树有 n n n 个节点。
第二行 n n n 个整数,依次表示每个节点的评分。
接下来 n − 1 n−1 n−1 行,每行 2 2 2 个整数 u , v u,v u,v,表示存在一条 u u u 到 v v v 的边。
由于这是一棵树,所以是不存在环的。
树的节点编号从 1 1 1 到 n n n。
输出格式:
输出一行一个数,表示上帝给这棵树的分数。
数据范围:
1 ≤ n ≤ 1 0 5 , 1≤n≤10^5, 1≤n≤105,
每个节点的评分的绝对值均不超过 1 0 6 10^6 106。
输入样例:
5
1 -2 -3 4 5
4 2
3 1
1 2
2 5
- 1
- 2
- 3
- 4
- 5
- 6
输出样例:
8
- 1
思路分析
状态表示
f [ u ] f[u] f[u]:在以u为根的子树中包含 u u u 的所有连通块的权值的最大值
状态计算
假设 s 1 , s 2 , … s k s_1,s_2,…s_k s1,s2,…sk 是 u u u 的孩子
f [ u ] = w [ u ] + m a x ( f [ s 1 ] , 0 ) + m a x ( f [ s 2 ] , 0 ) + … m a x ( f [ s k ] , 0 ) f[u]=w[u]+max(f[s_1],0)+max(f[s_2],0)+…max(f[s_k],0) f[u]=w[u]+max(f[s1],0)+max(f[s2],0)+…max(f[sk],0)
从根结点开始深度优先遍历每个子结点
代码
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010, M = N * 2;
int n;
int w[N];
int h[N], e[M], ne[M], idx;
LL f[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u, int father)
{
f[u] = w[u];
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j != father)
{
dfs(j, u);
f[u] += max(0ll, f[j]);
}
}
}
int main()
{
scanf("%d", &n);
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
for (int i = 0; i < n - 1; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
dfs(1, -1);
LL res = f[1];
for (int i = 2; i <= n; i ++ ) res = max(res, f[i]);
printf("%lld\n", res);
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
文章来源: chen-ac.blog.csdn.net,作者:辰chen,版权归原作者所有,如需转载,请联系作者。
原文链接:chen-ac.blog.csdn.net/article/details/122794410
- 点赞
- 收藏
- 关注作者


评论(0)