CSP 201512-4 送货
问题描述
为了增加公司收入, F F F 公司新开设了物流业务。
由于 F F F 公司在业界的良好口碑,物流业务一开通即受到了消费者的欢迎,物流业务马上遍及了城市的每条街道。
然而, F F F 公司现在只安排了小明一个人负责所有街道的服务。
任务虽然繁重,但是小明有足够的信心,他拿到了城市的地图,准备研究最好的方案。
城市中有 n n n 个交叉路口, m m m 条街道连接在这些交叉路口之间,每条街道的首尾都正好连接着一个交叉路口。
除开街道的首尾端点,街道不会在其他位置与其他街道相交。
每个交叉路口都至少连接着一条街道,有的交叉路口可能只连接着一条或两条街道。
小明希望设计一个方案,从编号为 1 1 1 的交叉路口出发,每次必须沿街道去往街道另一端的路口,再从新的路口出发去往下一个路口,直到所有的街道都经过了正好一次。
输入格式
输入的第一行包含两个整数 n , m n, m n,m,表示交叉路口的数量和街道的数量,交叉路口从 1 1 1 到 n n n 标号。
接下来 m m m 行,每行两个整数 a , b ( a ≠ b ) a, b(a \neq b) a,b(a=b),表示和标号为 a a a 的交叉路口和标号为 b b b 的交叉路口之间有一条街道,街道是双向的,小明可以从任意一端走向另一端。
两个路口之间最多有一条街道。
输出格式
如果小明可以经过每条街道正好一次,则输出一行包含 m + 1 m+1 m+1 个整数 p 1 , p 2 , p 3 , . . . , p m + 1 p_1, p_2, p_3,..., p_{m+1} p1,p2,p3,...,pm+1,表示小明经过的路口的顺序,相邻两个整数之间用一个空格分隔。
如果有多种方案满足条件,则输出字典序最小的一种方案,即首先保证 p 1 p_1 p1 最小, p 1 p_1 p1 最小的前提下再保证 p 2 p_2 p2 最小,依此类推。
如果不存在方案使得小明经过每条街道正好一次,则输出一个整数 − 1 -1 −1。
数据范围
前 30 % 30\% 30% 的评测用例满足: 1 ≤ n ≤ 10 , n − 1 ≤ m ≤ 20 1 ≤ n ≤ 10, n-1 ≤ m ≤ 20 1≤n≤10,n−1≤m≤20。
前 50 % 50\% 50% 的评测用例满足: 1 ≤ n ≤ 100 , n − 1 ≤ m ≤ 10000 1 ≤ n ≤ 100, n-1 ≤ m ≤ 10000 1≤n≤100,n−1≤m≤10000。
所有评测用例满足: 1 ≤ n ≤ 10000 , n − 1 ≤ m ≤ 100000 1 ≤ n ≤ 10000,n-1 ≤ m ≤ 100000 1≤n≤10000,n−1≤m≤100000。
输入样例1:
4 5
1 2
1 3
1 4
2 4
3 4
- 1
- 2
- 3
- 4
- 5
- 6
输出样例1:
1 2 4 1 3 4
- 1
样例1解释
城市的地图和小明的路径如下图所示。
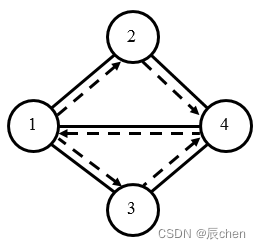
输入样例2:
4 6
1 2
1 3
1 4
2 4
3 4
2 3
- 1
- 2
- 3
- 4
- 5
- 6
- 7
输出样例2:
-1
- 1
样例2解释
城市的地图如下图所示,不存在满足条件的路径。
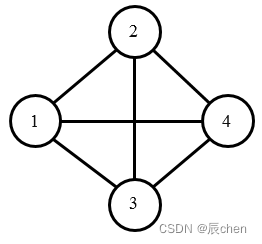
本题链接:http://118.190.20.162/view.page?gpid=T34
AC代码
C++
#include <iostream>
#include <cstring>
#include <algorithm>
#include <set>
using namespace std;
const int N = 10010, M = 100010;
int n, m;
set<int> g[N];
int p[N];
int ans[M], top;
int find(int x) // 并查集
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void dfs(int u)
{
while (g[u].size())
{
int t = *g[u].begin();
g[u].erase(t), g[t].erase(u); // 删边
dfs(t);
}
ans[ ++ top] = u;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化p数组
while (m -- )
{
int a, b;
scanf("%d%d", &a, &b);
g[a].insert(b), g[b].insert(a);
p[find(a)] = find(b);
}
int s = 0;
for (int i = 1; i <= n; i ++ )
if (find(i) != find(1)) // 不是连通图
{
puts("-1");
return 0;
}
else if (g[i].size() % 2) s ++ ; // s记录的是度数为奇数的点的
// 度数为奇数的点不是0个或2个,或者度数为奇数的点为2个但是起点的度数不是奇数,则不符合欧拉路径
if (s != 0 && s != 2 || s == 2 && g[1].size() % 2 == 0)
{
puts("-1");
return 0;
}
dfs(1); // 开始遍历欧拉路径
for (int i = top; i; i -- ) // 欧拉路径实际上记录的是倒序,故求正向欧拉路径需要逆序输出
printf("%d ", ans[i]);
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
java
注:java版代码只有50分
import java.util.*;
public class Main {
final int N = 100010;
int n, m;
int[] ans = new int[N];
int top;
int[] p = new int[10010];
TreeSet[] g = new TreeSet[10010];
void run() {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
for (int i = 0; i <= n; i++) {
g[i] = new TreeSet();
}
for (int i = 1; i <= n; i++) {
p[i] = i;
}
while (m -- != 0) {
int a, b;
a = sc.nextInt();
b = sc.nextInt();
g[a].add(b);
g[b].add(a);
p[find(a)] = find(b);
}
int s = 0;
for (int i = 1; i <= n; i++) {
if (find(i) != find(1)) {
System.out.println("-1");
return;
} else if (g[i].size() % 2 != 0) {
s++;
}
}
if (s != 0 && s != 2 || (s == 2 && g[1].size() % 2 == 0)) {
System.out.println("-1");
return;
}
dfs(1);
for (int i = top; i != 0; i--) {
System.out.printf("%d ", ans[i]);
}
}
void dfs(int u) {
while (g[u].size() != 0) {
int t = (Integer) g[u].first();
g[u].remove(t);
g[t].remove(u);
dfs(t);
}
ans[ ++ top] = u;
}
int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
public static void main(String[] args) {
new Main().run();
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
代码解释
从一个点出发,不重不漏的经过图中每一条边的一条路径(允许多次经过同一个点)。
从一个点出发,不重不漏的经过图中每一条边的一条路径(允许多次经过同一个点)。如果此路径的起点和终点相同,则称其为一条欧拉回路。
入度(indegree)就是有向图中指向这个点的边的数量,即有向图的某个顶点作为终点的次数和
出度(outdegree)就是从这个点出去的边的数量,即有向图的某个顶点作为起点的次数和
一个点的度(degree)指图中与该点相连的边数
无向连通图
欧拉回路:所有点的度数都为偶数即为有欧拉回路
欧拉路径:度数为奇数的点要么有2个要么有0个
若为0个那么从任意点出发都可以,如果有2个,那么起点必须是其中一个点,终点必须为另一个点
有向连通图
欧拉回路:所有点的入度等于出度
欧拉路径:1.所有点的入度等于出度 2.有一个点(终点)的入度=出度+1,且存在一个点(起点)的出度=入度+1
从当前点出发,只要有出去的边就往外走,深度优先遍历,回溯路径就是它的一个方案
为什么从起点搜到终点不是一个方案?
因为在搜索的过程中,不一定会把所有的边全部走到(有一堆额外的环),但因为起点和终点是唯一的,
且其余点的度数均为偶数,故我们在回溯的过程中把其他的结点(那些没有走过的环)补充到搜索图中即可
字典序最小:从当前点出去搜的时候,按照编号从小到大搜索一遍,就可以保证字典序最小
欧拉路径证明(无向图)
对于起点而言,设其度数为n,那么起始往出走需要一条边,其余到达起点的话,就必然是进来一次出去一次,故起点的度数必须是奇数
对于终点而言,设其度数为m,那么最终到达需要一条边,其余到达终点的点,需要再次出去,故终点的度数必须是奇数
对于非起点和非终点的其余点,它们只是作为中间的“桥梁”,故到达这些点后还需要离开,故这些点的度数必须是偶数
如果起点和终点是同一个点,那么对于起点(终点)而言,出去需要一条边,最终到达该点需要一条边,其余时候进来必然还要出去,
故在这种情况下,起点(终点)的度为偶数
综上所述,对于一个无向图的欧拉路径而言,度数为奇数的点要么为2个要么为0个,且为2个的时候,这两个点分别做起点和终点
dfs(u) // 求得的序列其实是欧拉路径的倒序序列
{
for u的所有边
dfs() // 扩展
seq += u // 把u加到序列中
}
- 1
- 2
- 3
- 4
- 5
- 6
欧拉路径dfs和一般图论dfs区别:
一般图论dfs用点来判重,时间复杂度在O(n+m)
欧拉路径是用边来判重,如果用一个bool变量来表示每个边是否被搜过,时间复杂度会很高:
举个例子,对于一个点,假设其有m条自环,那么我们在遍历的过程中搜第一条边,搜完之后又回到该点,
此时第一条边已经被用过了,故我们要跳过这一条边搜第二条边,依次类推,在搜第三条边的时候需要跳过第一条边和第二条边
以此类推,在搜完m条边的时候就会跳m^2次,这样对于1e5的数据量显然就会超时
处理方法:每用一条边不是进行简单的标记,而是直接进行删除,这样就可以降为线性时间复杂度
无向图的删除方法:因为建无向图对于每一条边会建立两次(不同方向),故我们在删除的时候还需要对它的反向边进行一次标记
如何根据一条边找到它的反向边:因为建边的时候是按照(0,1),(2,3)…进行建边,故求反向边可直接根据 i^1 求得
上述代码中并未采取这种建边方式,直接把边放入set中,set自然有序,且易直接删边
文章来源: chen-ac.blog.csdn.net,作者:辰chen,版权归原作者所有,如需转载,请联系作者。
原文链接:chen-ac.blog.csdn.net/article/details/124806082
- 点赞
- 收藏
- 关注作者


评论(0)