AcWing 272. 最长公共上升子序列

本题链接：AcWing 272. 最长公共上升子序列

本博客给出本题截图：

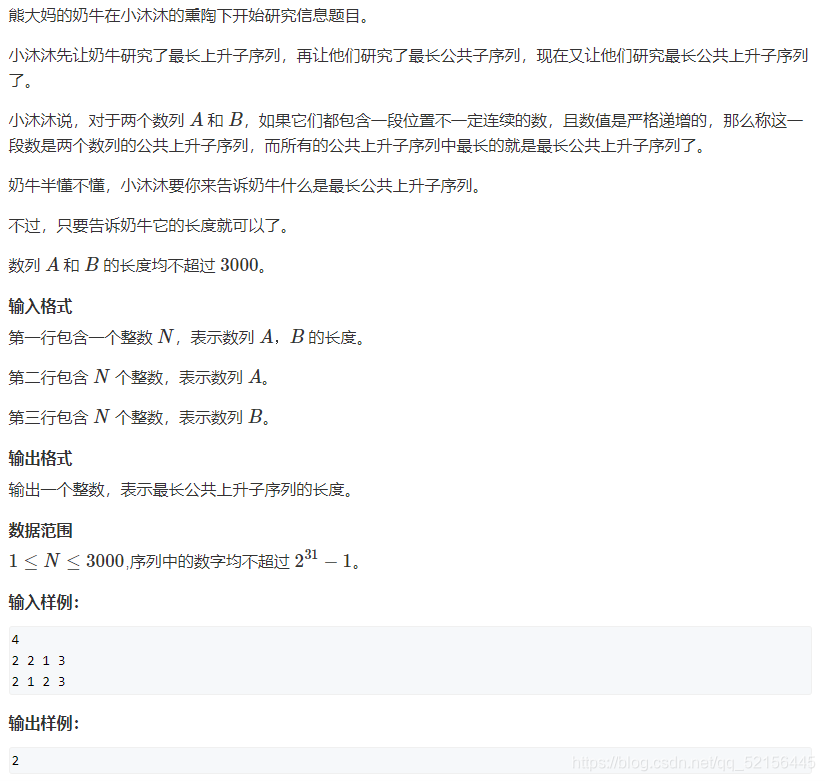
AC代码

代码解释：f[i][j]代表所有在a[1 ~n]和b[1 ~ n]中都出现过，并且以b[j]结尾的公共上升子序列的最大值的集合
如果不包含a[i]的话那么

f[i][j] = f[i - 1][j];

  
 

  
1
 

如果包含a[i]的话，那么我们现在的公共上升子序列必然最后一位是a[i] (b[j])，那么我们开始根据倒数第二位去继续划分，进行状态转移，那么我们假设这个子序列的倒数第二位是b[k] (k < j)，当k == 0时证明没有倒数第二位，即当前子序列只有一个数，即maxv = 1，然后k从 1 开始遍历到 j - 1，注意在遍历的过程中，只有满足 b[k] < b[j]才可以更新maxv

if (a[i] == b[j])
{
	int maxv = 1;
	for (int k = 1; k < j; k ++ )
		if (b[k] < b[j]) 
			maxv = max(maxv, f[i - 1][k] + 1);
	f[i][j] = max(f[i][j], maxv);
}

  
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

TLE版：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 3010;

int a[N], b[N], f[N][N];

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= n; i ++ ) cin >> b[i];

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j])
            {
                int maxv = 1;
                for (int k = 1; k < j; k ++ )
                    if (b[k] < b[j]) 
                        maxv = max(maxv, f[i - 1][k] + 1);
                f[i][j] = max(f[i][j], maxv);
            }
        }

    int res = 0;
    for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
    cout << res << endl;

    return 0;
}

  
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
 

代码优化：三重循环，TLE 也不太意外，如何去优化呢？从第三重循环去下手，我们发现，对于我们遍历的每一个j，第三重循环都会重新遍历一遍1 ~ j - 1，这样显然是有很多重复在其中的，我们如果可以每次都把1 ~ j - 1中的最大值给存储起来，那么当我们j ++后，下一次该遍历1 ~ j的时候，只需要用这个最大值再去和j去比较即可，故我们把maxv放到一重循环中，然后来观察那个TLE代码：

if (a[i] == b[j])
{
	int maxv = 1;
	for (int k = 1; k < j; k ++ )
		if (b[k] < b[j]) 
			maxv = max(maxv, f[i - 1][k] + 1);
	f[i][j] = max(f[i][j], maxv);
}

  
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

在这个代码中if (b[k] < b[j])可以替换为if (b[k] < a[i])，因为大前提是if (a[i] == b[j])，那么这个第三重的for循环就可以理解成在前j - 1中找到所有b[k] < a[i]的然后去更新，故当我们去掉第三重循环后可优化为：

if (a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);

  
 

  
1
 

AC代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 3010;

int a[N], b[N], f[N][N];

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= n; i ++ ) cin >> b[i];

    for (int i = 1; i <= n; i ++ )
    {
        int maxv = 1;
        for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
            if (a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);
        }
    }

    int res = 0;
    for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
    cout << res << endl;

    return 0;
}

  
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
 

文章来源: chen-ac.blog.csdn.net，作者：辰chen，版权归原作者所有，如需转载，请联系作者。

原文链接：chen-ac.blog.csdn.net/article/details/119893807