P4933 大师
【摘要】
P4933 大师
P4933 大师AC代码
P4933 大师
本题链接:P4933 大师
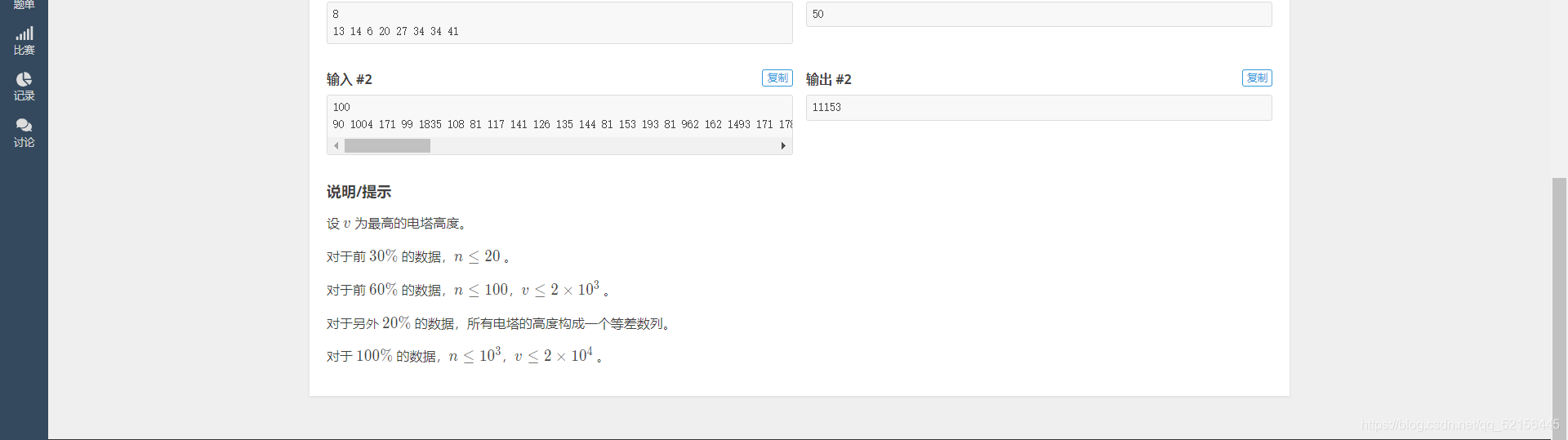
本博客给出本题截图:
AC代码
代码解释: f[i][j]代表的是在以第 i 项结尾...
P4933 大师
本题链接:P4933 大师
本博客给出本题截图:

AC代码
代码解释:
f[i][j]代表的是在以第 i 项结尾,公差为 j 的所有等差数列的数量,在这里我们可以知道,如果我们 j 按照从 1 ~ M 来暴力枚举,显然会 TLE 思考后会发现,我们如果只去枚举 h[i] - h[j] 即可,因为可能会有负数:递减的等差数列,故可能会有 h[i] - h[j] < 0,这里我们把数组开成两倍之后用 h[i] - h[j] + M / 2 即可
这里提一下状态转移方程:
f[i][t] = (f[i][t] + f[j][t] + 1) % mol;
- 1
这里为什么要 + 1,可以理解成 在所有的以 j 结尾的数列多加一个 i ,再加上单独由 j 和 i 组成的这么一组数列
注意 dp 过程中我们不讨论只有一个电塔的情况,故我们的 res 初始化为 n
代码:
#include <cstdio>
#include <algorithm>
using namespace std;
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1010, mol = 998244353, M = 40010;
int h[N];
int f[N][M];
int n;
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
int res = n;
for (int i = 1; i <= n; i ++ )
{
for (int j = i - 1; j; j -- )
{
auto t = h[i] - h[j] + M / 2;
f[i][t] = (f[i][t] + f[j][t] + 1) % mol;
res = (res + f[j][t] + 1) % mol;
}
}
printf("%d\n", res);
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
文章来源: chen-ac.blog.csdn.net,作者:辰chen,版权归原作者所有,如需转载,请联系作者。
原文链接:chen-ac.blog.csdn.net/article/details/119842571
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)