P3205 [HNOI2010]合唱队

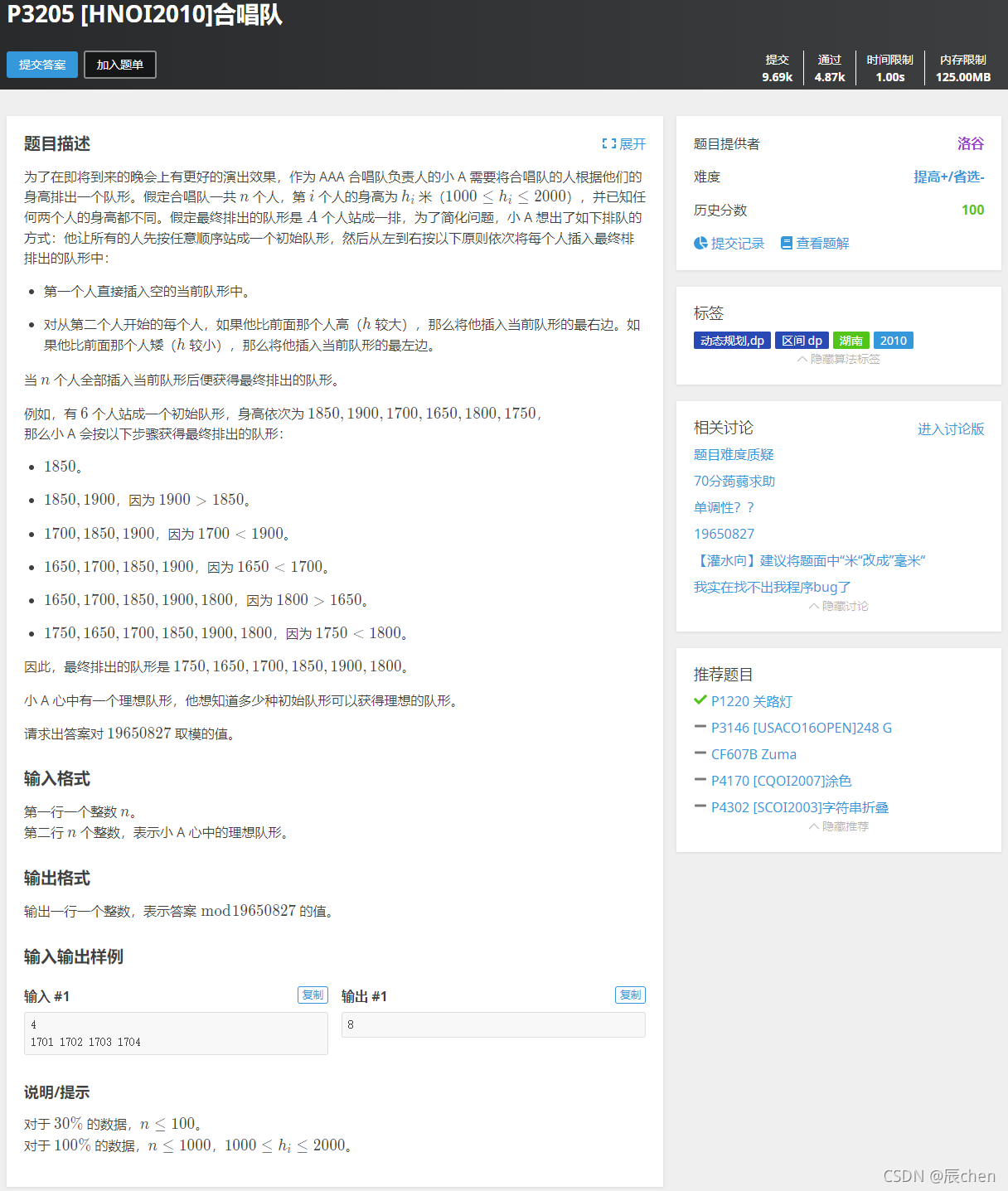
本题链接：P3205 [HNOI2010]合唱队

本博客给出本题截图：

AC代码

代码解释：和 P1220 关路灯 同一类型的题目，问题的关键还是状态转移方程的思路，我们会发现，对于我们的理想队形，我们每次往理想队形中插入一个人的时候，只有可能往最左边或者最右边去插入，这就意味着，我们插入的人肯定是队伍的最两边的，我们都知道，往队伍的左右插入是由 上一个插入的人的身高作比较 得到的结果，又由于每次的插入都是只能往队伍的最左边或者是最右边插入人，上一个插入的人其实是队伍的最左侧和最右侧(不包括我们即将插入的人
这个题目是分成往队伍的最左边插入和队伍的最右边插入两种不同的情况，可以用一个三维数组去形象的表示：
f[i][j][0]表示的是把第i个人插入到队伍的最左边
f[i][j][1]表示的是把第j个人插入到队伍的最右边
那么这个动态转移方程的表达也显得十分的显而易见了，只有符合我们的里相队形才会进行状态转移：

if (h[i] < h[i + 1]) f[i][j][0] += f[i + 1][j][0];
if (h[i] < h[j]) f[i][j][0] += f[i + 1][j][1];
if (h[j] > h[i]) f[i][j][1] += f[i][j - 1][0];
if (h[j] > h[j - 1]) f[i][j][1] += f[i][j - 1][1];

  

 

  
1
  
2
  
3
  
4
 

这里需要注意，每次进行转移的时候，我们都需要进行取模，且在输出最终答案的时候也是需要取模的：

cout << (f[1][n][0] + f[1][n][1]) % mol << endl;

  

 

  
1
 

最后来说一下数组的初始化，在我们的队列中只有一个人的时候，显然这是不分插入到最左边或者是插入到最右边的，我们可以自己规定一下，我们在插入第一个人的时候，统一默认成是往左边插入，那么代码为：

for (int i = 1; i <= n; i ++ ) f[i][i][0] = 1;

  

 

  
1
 

显然，你也可以规定是往最右边插入，这都是可以的，但是你不可以规定为f[i][i][0] = f[i][i][1] = 1，这显然就是错误的了，这就会把每次的插入第一个人的操作计算成两种情况：即插入第一人从最左边插入和从最右边插入两种情况。但其为一种情况.

代码：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, mol = 19650827;

int h[N];
int f[N][N][2];

int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i ++ ) cin >> h[i];
	
	for (int i = 1; i <= n; i ++ ) f[i][i][0] = 1;
	
	for (int l = 1; l <= n; l ++ )
		for (int i = 1, j = l + i; j <= n; i ++, j ++ )
		{
			if (h[i] < h[i + 1]) f[i][j][0] += f[i + 1][j][0];
			if (h[i] < h[j]) f[i][j][0] += f[i + 1][j][1];
			if (h[j] > h[i]) f[i][j][1] += f[i][j - 1][0];
			if (h[j] > h[j - 1]) f[i][j][1] += f[i][j - 1][1];
			f[i][j][0] %= mol; 
			f[i][j][1] %= mol;
		}
	
	cout << (f[1][n][0] + f[1][n][1]) % mol << endl;
	
	return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
 

文章来源: chen-ac.blog.csdn.net，作者：辰chen，版权归原作者所有，如需转载，请联系作者。

原文链接：chen-ac.blog.csdn.net/article/details/120824011