前言

蓝桥杯官网：蓝桥杯大赛——全国大学生TMT行业赛事
✨本博客讲解 蓝桥杯C/C++ 备赛所涉及算法知识，此博客为第十一讲：双指针【例/习题】

本篇博客所包含习题有：
👊日志统计
👊完全二叉树的权值
👊递增三元组

博客内容以题代讲，通过讲解题目的做法来帮助读者快速理解算法内容，需要注意：学习算法不能光过脑，更要实践，请读者务必自己敲写一遍本博客相关代码！！！

日志统计

来源： 第九届蓝桥杯省赛C++B组,第九届蓝桥杯省赛JAVAB组

题目要求

题目描述：

小明维护着一个程序员论坛。现在他收集了一份”点赞”日志，日志共有 $N$ 行。

其中每一行的格式是：

ts id  

  

 

  
1
 

表示在 $ts$ 时刻编号 $id$ 的帖子收到一个”赞”。

现在小明想统计有哪些帖子曾经是”热帖”。

如果一个帖子曾在任意一个长度为 $D$ 的时间段内收到不少于 $K$ 个赞，小明就认为这个帖子曾是”热帖”。

具体来说，如果存在某个时刻 $T$ 满足该帖在 $[T,T+D)$ 这段时间内(注意是左闭右开区间)收到不少于 $K$ 个赞，该帖就曾是”热帖”。

给定日志，请你帮助小明统计出所有曾是”热帖”的帖子编号。

输入格式：

第一行包含三个整数 $N,D,K$。

以下 $N$ 行每行一条日志，包含两个整数 $ts$ 和 $id$。

输出格式：

按从小到大的顺序输出热帖 $id$。

每个 $id$ 占一行。

数据范围：

$1\le K\le N\le 10^5,$
$0\le ts,id\le 10^5,$
$1\le D\le 10000$

输入样例：

7 10 2
0 1
0 10
10 10
10 1
9 1
100 3
100 3

输出样例：

1
3

思路分析

$logs$ 数组存储的是日志信息，$cnt[i]$ 表示的是 $id$ 为 $i$ 的帖子在一段时间内的获赞量，$st[i]$ 用来判断 $id$ 为 $i$ 的帖子是否曾经是个热帖，如果是，那么有：st[i] = true;，否则有：st[i] = false;，本题的双指针在于用 $i$ 和 $j$ 表示一段时间，每次取出新增的 $id$，然后让这个 $id$ 的 cnt[id] ++;，然后判断此时的时间跨度是否大于了规定的 $D$，如果大于，那么就让 $j$ 向后挪动一格，因为挪动后原先的 $j$ 就不在段时间的范围内，故有：cnt[logs[j].y] --;，挪动后判断新增的这个 $id$ 是否有：cnt[id] >= k，若有，则证明这个 $id$ 是一个热帖：st[id] = true;，最后遍历所有的 $id$，把符合的 $id$ 输出即可。

代码

#include <cstdio>
#include <cstring>
#include <algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;

const int N = 100010;

PII logs[N];
int cnt[N];
bool st[N];

int main()
{
    int n, d, k;
    scanf("%d%d%d", &n, &d, &k);
    for (int i = 0; i < n; i ++ ) scanf("%d%d", &logs[i].x, &logs[i].y);
    
    sort(logs, logs + n);
    
    for (int i = 0, j = 0; i < n; i ++ ) 
    {
        int id = logs[i].y;
        cnt[id] ++;
        
        while (logs[i].x - logs[j].x >= d)
        {
            cnt[logs[j].y] --;
            j ++;
        }
        
        if (cnt[id] >= k) st[id] = true;
    }
    
    for (int i = 0; i <= 100000; i ++ ) 
        if (st[i]) printf("%d\n", i);
        
    return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
 

完全二叉树的权值

来源： 第十届蓝桥杯省赛C++A/B组,第十届蓝桥杯省赛JAVAA组

题目要求

题目描述：

给定一棵包含 $N$ 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是 $A_1,A_2,\cdot \cdot \cdot A_N$，如下图所示：

现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？

如果有多个深度的权值和同为最大，请你输出其中最小的深度。

注：根的深度是 $1$。

输入格式：

第一行包含一个整数 $N$。

第二行包含 $N$ 个整数 $A_1,A_2,\cdot \cdot \cdot A_N$。

输出格式：

输出一个整数代表答案。

数据范围：

$1\le N\le 10^5,$
$-10^5\le A_i\le 10^5$

输入样例：

7
1 6 5 4 3 2 1

输出样例：

2

思路分析

我们一层一层的去遍历，对于构造一个完全二叉树，我们可以按照如下进行构造：

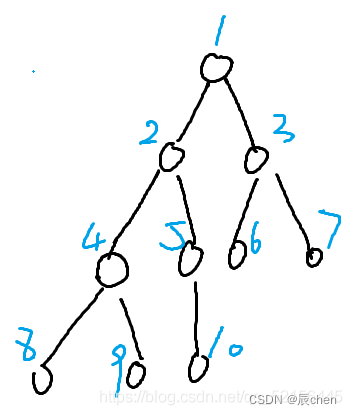
即数组从 $1$ 开始进行，那么对于一个结点 $i$，$i\times 2$ 就是左儿子，$i\times 2+1$ 就是右儿子，不难看出，假设此时的深度为 $d$，那么这层的最左边的儿子的编号 $i=2^{d-1}$，该层的节点编号 $j\in [i,i+2^{d-1})$，故我们可以一层一层的遍历，每次都计算每一层的点数之和，用 $Max$ 记录点数和的最大值，用 $depth$ 记录点数最大的层数。本题代码虽然有两层循环，但是其实每一个节点只会遍历一次，故本题代码的时间复杂度为 $O(n)$

代码

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010;

int a[N];

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    
    LL Max = -1e18;
    int depth = 0;
    for (int d = 1, i = 1; i <= n; i *= 2, d ++ )    //遍历每一层
    {
        LL temp = 0;
        for (int j = i; j < i + (1 << d - 1) && j <= n; j ++ )
            temp += a[j];
            
        if (temp > Max)
        {
            Max = temp;
            depth = d;
        }
    }
    
    printf("%d\n", depth);
    
    return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
 

递增三元组

来源： 第九届蓝桥杯省赛C++B组,第九届蓝桥杯省赛JAVAB组

题目要求

题目描述：

给定三个整数数组

$A=[A_1,A_2,\dots A_N],$
$B=[B_1,B_2,\dots B_N],$
$C=[C_1,C_2,\dots C_N],$

请你统计有多少个三元组 $(i,j,k)$ 满足：

$1\le i,j,k\le N$
$A_i<B_j<C_k$

输入格式：

第一行包含一个整数 $N$。

第二行包含 $N$ 个整数 $A_1,A_2,\dots A_N$。

第三行包含 $N$ 个整数 $B_1,B_2,\dots B_N$。

第四行包含 $N$ 个整数 $C_1,C_2,\dots C_N$。

输出格式：

一个整数表示答案。

数据范围：

$1\le N\le 10^5,$
$0\le A_i,B_i,C_i\le 10^5$

输入样例：

3
1 1 1
2 2 2
3 3 3

输出样例：

27

思路分析

本题有三种解法，本博客只讲解双指针的解法，对于前缀和、二分的解法见博客：蓝桥杯第八讲–枚举与模拟【例题】

双指针的解法同二分类似，先对三个数组分别进行排序，然后遍历 $b$数组，其中 $i,j,k$ 分别是 $a,b,c$数组的指针，对于每一个 $b[j]$，对数组$a$ 的操作为：while (i < n && a[i] < b[j]) i ++;，特别注意，执行完这句时候，$i$ 指针停留的位置其实是第一个大于等于 $b[j]$ 的位置，即从 $0$ ~ $i-1$ 是符合题意的，对数组$c$ 的操作为：while (k < n && c[k] <= b[j]) k ++;，执行完这行代码，$k$ 停留的位置即第一个大于 $b[j]$ 的位置，即从 $k$ ~ $n-1$ 是符合题意的，故我们用 res += i * (n - 1 - k + 1);。接着分析本题是否会爆 $int$：如果数组 $A,B,C$ 正好是统一单调递增的，那么这个时候三元组的数量约为：$N\times N=10^{10}$，即本题会爆 $int$，故我们的 $res$ 用 $long$ $long$ 去存。

代码

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010;

int n;
int a[N], b[N], c[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    for (int i = 0; i < n; i ++ ) scanf("%d", &b[i]);
    for (int i = 0; i < n; i ++ ) scanf("%d", &c[i]);
    
    sort(a, a + n);
    sort(b, b + n);
    sort(c, c + n);
    
    LL res = 0;
    for (int i = 0, j = 0, k = 0; j < n; j ++ )
    {
        while (i < n && a[i] < b[j]) i ++;
        while (k < n && c[k] <= b[j]) k ++;
        res += (LL)i * (n - 1 - k + 1);
    }
    
    printf("%lld\n", res);
    
    return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
 

文章来源: chen-ac.blog.csdn.net，作者：辰chen，版权归原作者所有，如需转载，请联系作者。

原文链接：chen-ac.blog.csdn.net/article/details/122782117