前言

蓝桥杯官网：蓝桥杯大赛——全国大学生TMT行业赛事
✨本博客讲解 蓝桥杯C/C++ 备赛所涉及算法知识，此博客为第十三讲：树状数组与线段树【例题】

本篇博客所包含习题有：
👊动态求连续区间和
👊数星星
👊数列区间最大值

树状数组与线段树【习题】见博客：蓝桥杯第十三讲–树状数组与线段树【习题】

注： 蓝桥杯对于树状数组与线段树的考察十分的基础简单，且历年只考察过两道题目，读者不需要了解其原理，只需要背诵模板学会调用即可。如果想要知道具体实现方式，见博客：树状数组，线段树（一），线段树（二） 【尚未更新】

博客内容以题代讲，通过讲解题目的做法来帮助读者快速理解算法内容，需要注意：学习算法不能光过脑，更要实践，请读者务必自己敲写一遍本博客相关代码！！！

动态求连续区间和

题目要求

题目描述：

给定 $n$ 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 $[a,b]$ 的连续和。

输入格式：

第一行包含两个整数 $n$ 和 $m$，分别表示数的个数和操作次数。

第二行包含 $n$ 个整数，表示完整数列。

接下来 $m$ 行，每行包含三个整数 $k,a,b$ （$k=0$，表示求子数列 $[a,b]$ 的和；$k=1$，表示第 $a$ 个数加 $b$）。

数列从 $1$ 开始计数。

输出格式：

输出若干行数字，表示 $k=0$ 时，对应的子数列 $[a,b]$ 的连续和。

数据范围：

$1\le n\le 100000,$
$1\le m\le 100000，$
$1\le a\le b\le n,$
数据保证在任何时候，数列中所有元素之和均在 $int$ 范围内。

输入样例：

10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
 

输出样例：

11
30
35

  

 

  
1
  
2
  
3
 

思路分析

本题用 树状数组 以及 线段树 两种方法去写，同时介绍模板

树状数组

使用树状数组会让时间复杂度变为：$O(\log n)$ 树状数组作用有两个：

• 让某个位置上的数加上一个数（单点修改）
• 求一个前缀和（区间查询）

当然，树状数组还有其他功能，但是对于蓝桥杯而言，只需要掌握以上两种即可

树状数组虽然是一维的，但是我们可以把它理解为是二维的，类似树的结构，如下图所示：

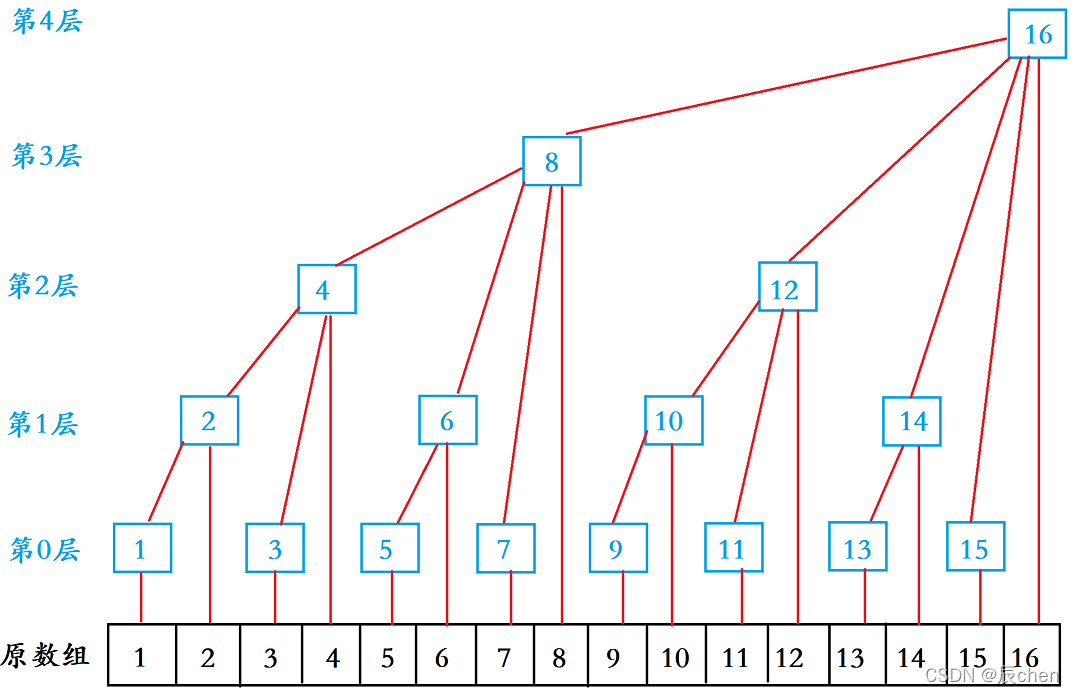
这里有几个需要注意的点：

1. 树状数组必须从 $1$ 开始
2. 虽然看起来是二维的类似树的结构，但是存储还是一维数组的形式
3. 上图中黑色的是原数组，蓝色的是树状数组
4. 红色的线代表的是数组之间的关系，比如 $2$ 与 $1$ 和 $2$ 相连，就代表着，树状数组 $2$ 由树状数组 $1$ 和原数组 $2$ 相加得到。而树状数组 $1$ 就是原数组 $1$ ；再举个例子：$16$ = $8$ + $12$ + $14$ + $15$ + $16$

以上就是对树状数组的一些定义说明，读者 不需要 知道为什么这么定义以及其中细节，感兴趣的可以看博客：树状数组 【尚未更新】，里面会有讲解。

下面介绍树状数组的几个基本函数：

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int v)      // 往 x 的位置加上一个数字 v
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

int query(int x)           // 求 [1, x] 原数组的前缀和
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];

    return res;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
 

上述代码需要：背背背！！！

代码(树状数组)

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1000010;

int n, m;
int a[N], tr[N];

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int v)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

int query(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++ ) add(i, a[i]);

    while(m -- )
    {
        int k, x, y;
        scanf("%d%d%d", &k, &x, &y);
        if (k == 0) printf("%d\n", query(y) - query(x - 1));
        else add(x, y);
    }

    return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
 

线段树

使用树状数组会让时间复杂度变为：$O(\log n)$ ，线段树的作用特别之多，包含树状数组的所有功能并且有很多额外的功能，但是代码相较与树状数组而言比较冗长。

线段树可以简单的理解成一个二叉树：

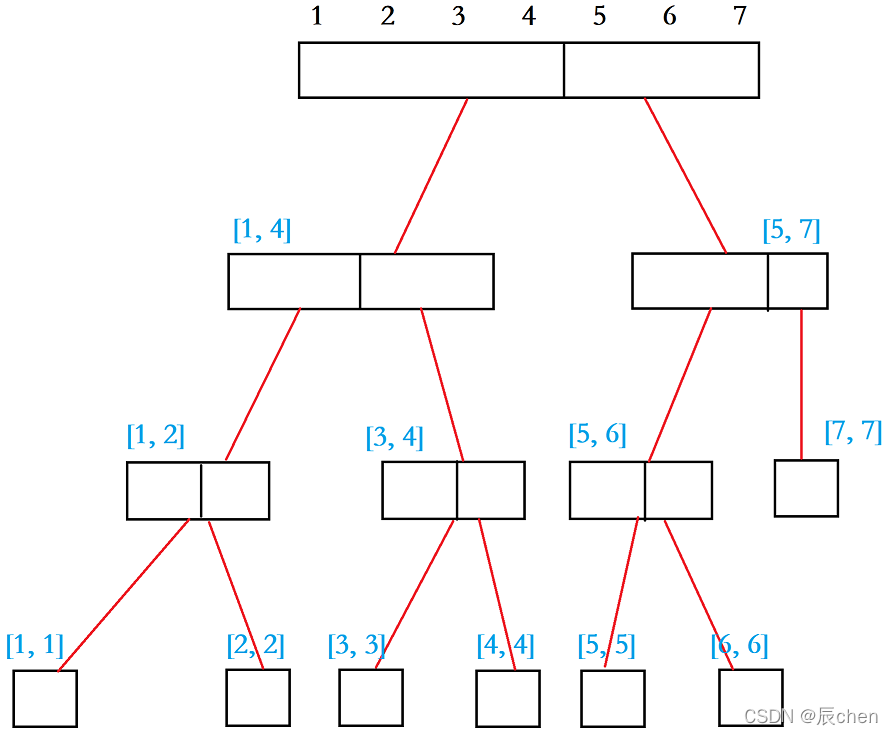
即线段树是对一段的数组，每次均分为两份，一直均分直到不能均分，红线代表的是求和的过程。

原理不进行讲解，读者 不需要 知道为什么这么定义以及其中细节，感兴趣的可以看博客：线段树（一），线段树（二） 【尚未更新】，里面会有讲解。

下面介绍线段树的几个函数：

struct Node
{
    int l, r;    // 涵盖范围，如上图中的蓝色字体就是l，r的取值
    int sum;
}tr[4 * N];      // 需要开题目要求的4倍大小，不需要知道其原理

void pushup(int u)        // 动态维护线段树
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void build(int u, int l, int r)   // 建一个线段树，u为根，l和r代表两个子树的涵盖范围
{
    if (l == r) tr[u] = {l, r, w[l]};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

int query(int u, int l, int r)    // 查询操作，求[l, r]的和，可以换为别的，核心是递归
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    int mid = tr[u].l + tr[u].r >> 1;
    int sum = 0;
    if (l <= mid) sum = query(u << 1, l, r);
    if (r > mid) sum += query(u << 1 | 1, l, r);
    return sum;
}

void modify(int u, int x, int v)// 修改操作，把x的位置的值加上一个v，可以换为别的，核心是递归
{
    if (tr[u].l == tr[u].r) tr[u].sum += v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
 

代码(线段树)

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int w[N];
struct Node
{
    int l, r;
    int sum;
}tr[4 * N];

void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l, r, w[l]};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    int mid = tr[u].l + tr[u].r >> 1;
    int sum = 0;
    if (l <= mid) sum = query(u << 1, l, r);
    if (r > mid) sum += query(u << 1 | 1, l, r);
    return sum;
}

void modify(int u, int x, int v)
{
    if (tr[u].l == tr[u].r) tr[u].sum += v;
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
    build(1, 1, n);

    int k, a, b;
    while (m -- )
    {
        scanf("%d%d%d", &k, &a, &b);
        if (k == 0) printf("%d\n", query(1, a, b));
        else modify(1, a, b);
    }

    return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
 

数星星

题目要求

题目描述：

天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。

如果一个星星的左下方（包含正左和正下）有 $k$ 颗星星，就说这颗星星是 $k$ 级的。

例如，上图中星星 $5$ 是 $3$ 级的（$1,2,4$ 在它左下），星星 $2,4$ 是 $1$ 级的。

例图中有 $1$ 个 $0$ 级，$2$ 个 $1$ 级，$1$ 个 $2$ 级，$1$ 个 $3$ 级的星星。

给定星星的位置，输出各级星星的数目。

换句话说，给定 $N$ 个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

输入格式：

第一行一个整数 $N$，表示星星的数目；

接下来 $N$ 行给出每颗星星的坐标，坐标用两个整数 $x,y$ 表示；

不会有星星重叠。星星按 $y$ 坐标增序给出，$y$ 坐标相同的按 $x$ 坐标增序给出。

输出格式：

$N$ 行，每行一个整数，分别是 $0$ 级，$1$ 级，$2$ 级，……，$N-1$ 级的星星的数目。

数据范围：

$1\le N\le 15000,$
$0\le x,y\le 32000$

输入样例：

5
1 1
5 1
7 1
3 3
5 5

  

 

  
1
  
2
  
3
  
4
  
5
  
6
 

输出样例：

1
2
1
1
0

  

 

  
1
  
2
  
3
  
4
  
5
 

思路分析

对于一颗星星的等级是查看这个星星的下方和左方有多少颗星星，因为我们的输入是从下到上，从左到右进行输入的，所以我们在对于每一颗星星进行统计的时候，可以边输入边计算，因为这样我们就只需要考虑横坐标的星星，即对于一颗横坐标为 $x$ 的星星，我们在输入它后，只需要查看一下从位置 $1$ ~ $x$ （树状数组要求从 $1$ 开始，但是我们的数据范围可以取到 $0$，故我们直接让 x ++; 即可）有多少颗星星即可，这样就转化为了一个求前缀和的问题，因为整个前缀和的过程是动态的，所以我们使用树状数组进行优化，因为我们的代码思路是边输入边进行统计，这样构造线段树的话会有些麻烦，故本题建议使用树状数组而不是线段树。 $level[i]$ 表示的就是等级为 $i$ 的星星的个数。

代码

#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 32010;

int n;
int tr[N], level[N];

int lowbit(int x)
{
    return x & -x;
}

void add(int x)
{
    for (int i = x; i < N; i += lowbit(i)) tr[i] ++;
}

int query(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    
    return res;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) 
    {
        int x, y;
        scanf("%d%d", &x, &y);
        x ++;
        level[query(x)] ++;
        add(x);
    }
    
    for (int i = 0; i < n; i ++ ) printf("%d\n", level[i]);
    
    return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
 

数列区间最大值

题目要求

题目描述：

输入一串数字，给你 $M$ 个询问，每次询问就给你两个数字 $X,Y$，要求你说出 $X$ 到 $Y$ 这段区间内的最大数。

输入格式：

第一行两个整数 $N,M$ 表示数字的个数和要询问的次数；

接下来一行为 $N$ 个数；

接下来 $M$ 行，每行都有两个整数 $X,Y$。

输出格式：

输出共 $M$ 行，每行输出一个数。

数据范围：

$1\le N\le 10^5,$
$1\le M\le 10^6,$
$1\le X\le Y\le N,$
数列中的数字均不超过$2^{31}-1$

输入样例：

10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8

  

 

  
1
  
2
  
3
  
4
 

输出样例：

5
8

  

 

  
1
  
2
 

思路分析

本题求的是最大值，和前缀和无关，即我们用树状数组无法解决问题，那么我们就可以使用线段树去解决本题，代码和本博客的第一道例题：动态求连续区间和 是类似的，只需要对求和部分改成求最大值就可以了，其中代码中出现了：$INT\_MIN$，这代表的是整数的最小值，即极小值，调用该函数需要加头文件：#include <climits>

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <climits>

using namespace std;

const int N = 100010;

int n, m;
int w[N];
struct Node
{
    int l, r;
    int maxv;
}tr[4 * N];

void pushup(int u)
{
    tr[u].maxv = max(tr[u << 1].maxv, tr[u << 1 | 1].maxv);
}

void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l ,r, w[l]};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].maxv;
    int mid = tr[u].l + tr[u].r >> 1;
    int maxv = INT_MIN;
    if (l <= mid) maxv = max(maxv, query(u << 1, l ,r));
    if (r > mid) maxv = max(maxv, query(u << 1 | 1, l, r));
    return maxv;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
    build(1, 1, n);
    
    int l, r;
    while (m -- )
    {
        scanf("%d%d", &l, &r);
        printf("%d\n", query(1, l, r));
    }
    
    return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
 

文章来源: chen-ac.blog.csdn.net，作者：辰chen，版权归原作者所有，如需转载，请联系作者。

原文链接：chen-ac.blog.csdn.net/article/details/122793618