蓝桥杯第十三讲--树状数组与线段树【习题】

举报
辰chen 发表于 2022/06/15 00:12:46 2022/06/15
【摘要】 文章目录 前言小朋友排队题目要求思路分析代码 油漆面积题目要求思路分析代码 前言 蓝桥杯官网：蓝桥杯大赛——全国大学生TMT行业赛事 ✨本博客讲解 蓝桥杯C/C++ 备赛所涉及算法...

文章目录

前言

蓝桥杯官网：蓝桥杯大赛——全国大学生TMT行业赛事
✨本博客讲解 蓝桥杯C/C++ 备赛所涉及算法知识，此博客为第十三讲：树状数组与线段树【习题】

本篇博客所包含习题有：
👊小朋友排队
👊油漆面积

树状数组与线段树【例题】见博客：蓝桥杯第十三讲–树状数组与线段树【例题】

注： 蓝桥杯对于树状数组与线段树的考察十分的基础简单，且历年只考察过两道题目，读者不需要了解其原理，只需要背诵模板学会调用即可。如果想要知道具体实现方式，见博客：树状数组，线段树（一），线段树（二） 【尚未更新】

博客内容以题代讲，通过讲解题目的做法来帮助读者快速理解算法内容，需要注意：学习算法不能光过脑，更要实践，请读者务必自己敲写一遍本博客相关代码！！！

小朋友排队

来源： 第五届蓝桥杯省赛C++B/C组

题目要求

题目描述：

n n n 个小朋友站成一排。

现在要把他们按身高从低到高的顺序排列，但是每次只能交换位置相邻的两个小朋友。

每个小朋友都有一个不高兴的程度。

开始的时候，所有小朋友的不高兴程度都是 0 0 0。

如果某个小朋友第一次被要求交换，则他的不高兴程度增加 1 1 1，如果第二次要求他交换，则他的不高兴程度增加 2 2 2（即不高兴程度为 3 3 3），依次类推。当要求某个小朋友第 k k k 次交换时，他的不高兴程度增加 k k k。

请问，要让所有小朋友按从低到高排队，他们的不高兴程度之和最小是多少。

如果有两个小朋友身高一样，则他们谁站在谁前面是没有关系的。

输入格式：

输入的第一行包含一个整数 n n n，表示小朋友的个数。

第二行包含 n n n 个整数 H 1 , H 2 , … , H n H_1,H_2,…,H_n H1​,H2​,…,Hn​，分别表示每个小朋友的身高。

输出格式：

输出一行，包含一个整数，表示小朋友的不高兴程度和的最小值。

数据范围：

1 ≤ n ≤ 100000 , 1≤n≤100000 , 1≤n≤100000,
0 ≤ H i ≤ 1000000 0≤H_i≤1000000 0≤Hi​≤1000000

输入样例：

3
3 2 1

  
 
    
  
  • 1
    • 
  
  • 2
    •

输出样例：

9

  
 
    
  
  • 1
    •

样例解释：
首先交换身高为 3 3 3 和 2 2 2 的小朋友，再交换身高为 3 3 3 和 1 1 1 的小朋友，再交换身高为 2 2 2 和 1 1 1 的小朋友，每个小朋友的不高兴程度都是 3 3 3，总和为 9 9 9。

思路分析

蓝桥杯历史上唯一一次考过的树状数组的题目。这个题本质上就是一道求逆序对的题目，且遵照冒泡排序的规则：因为只能交换相邻的两个孩子，且只要存在一个逆序对，我们要把所有孩子的身高按照从低到高进行排序的话，那么就必然会存在至少一次交换，即假设有 k k k 个逆序对，那么交换的次数就至少是 k k k，且在冒泡排序中，每次必然是相邻两个为逆序对的时候才会发生交换，故假设有 k k k 个逆序对，我们就会交换 k k k 次。故我们可以用树状数组去维护这个动态区间，即先从前往后构造树状数组，构造的过程中，每次插入一个 h [ i ] h[i] h[i]，我们都统计一下在已插入的数中有多少个数比它大，我们知道树状数组其实维护的是一个前缀和，那么大于 h [ i ] h[i] h[i] 的其实就是：query(N - 1) - query(h[i]);，我们用 s u m [ i ] sum[i] sum[i] 来记录 i i i 这个小朋友被交换的次数，然后我们还需要清空树状数组再做一次：从后往前建树状数组，看后面有多少个数比当前的数小，即：query(h[i] - 1);，最后对于每一个小朋友都计算一次 1 + 2 + . . . + s u m [ i ] 1+2+...+sum[i] 1+2+...+sum[i]，用高斯求和： ( 1 + s u m [ i ] ) × s u m [ i ] / 2 (1+sum[i])\times sum[i] / 2 (1+sum[i])×sum[i]/2，最后把和累加即可，这里需要注意，因为逆序对的个数最大值是 1 e 5 1e5 1e5，故上述式子会爆 i n t int int，故本题答案 r e s res res 需要用 l o n g long long l o n g long long 去存。

代码

#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 1000010;

int n;
int h[N], tr[N];
int sum[N];

int lowbit(int x)
{
    return x & -x;
}

void add(int x, int v)
{
    for (int i = x; i < N; i += lowbit(i)) tr[i] += v;
}

int query(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &h[i]), h[i] ++;
    
    // 求前面有多少个数比它大
    for (int i = 0; i < n; i ++ ) 
    {
        sum[i] = query(N - 1) - query(h[i]);
        add(h[i], 1);
    }
    
    // 求后面有多少个数比它小
    memset(tr, 0, sizeof tr);
    for (int i = n - 1; ~i; i -- )
    {
        sum[i] += query(h[i] - 1);
        add(h[i], 1);
    }
    
    LL res = 0;
    for (int i = 0; i < n; i ++ ) res += (LL)sum[i] * (sum[i] + 1) / 2;
    
    printf("%lld\n", res);
    
    return 0;
}

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    • 
  
  • 56
    • 
  
  • 57
    • 
  
  • 58
    •

油漆面积

来源： 第八届蓝桥杯省赛C++A组,第八届蓝桥杯省赛JAVAA组

题目要求

题目描述：

X X X星球的一批考古机器人正在一片废墟上考古。

该区域的地面坚硬如石、平整如镜。

管理人员为方便，建立了标准的直角坐标系。

每个机器人都各有特长、身怀绝技。

它们感兴趣的内容也不相同。

经过各种测量，每个机器人都会报告一个或多个矩形区域，作为优先考古的区域。

矩形的表示格式为 ( x 1 , y 1 , x 2 , y 2 ) (x_1,y_1,x_2,y_2) (x1​,y1​,x2​,y2​)，代表矩形的两个对角点坐标。

为了醒目，总部要求对所有机器人选中的矩形区域涂黄色油漆。

小明并不需要当油漆工，只是他需要计算一下，一共要耗费多少油漆。

其实这也不难，只要算出所有矩形覆盖的区域一共有多大面积就可以了。

注意，各个矩形间可能重叠。

输入格式：

第一行，一个整数 n n n，表示有多少个矩形。

接下来的 n n n 行，每行有 4 4 4 个整数 x 1 , y 1 , x 2 , y 2 x_1,y_1,x_2,y_2 x1​,y1​,x2​,y2​，空格分开，表示矩形的两个对角顶点坐标。

输出格式：

一行一个整数，表示矩形覆盖的总面积。

数据范围：

1 ≤ n ≤ 10000 , 1≤n≤10000 , 1≤n≤10000,
0 ≤ x 1 , x 2 , y 2 , y 2 ≤ 10000 0≤x_1,x_2,y_2,y_2≤10000 0≤x1​,x2​,y2​,y2​≤10000
数据保证 x 1 < x 2 x_1<x_2 x1​<x2​ 且 y 1 < y 2 y_1<y_2 y1​<y2​。

输入样例1：

3
1 5 10 10
3 1 20 20
2 7 15 17

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    •

输出样例1：

340

  
 
    
  
  • 1
    •

输入样例2：

3
5 2 10 6
2 7 12 10
8 1 15 15

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    •

输出样例2：

128

  
 
    
  
  • 1
    •

思路分析

蓝桥杯历史上唯一一次考过的线段树的题目。本题求法如下图所示，用扫描线进行优化：
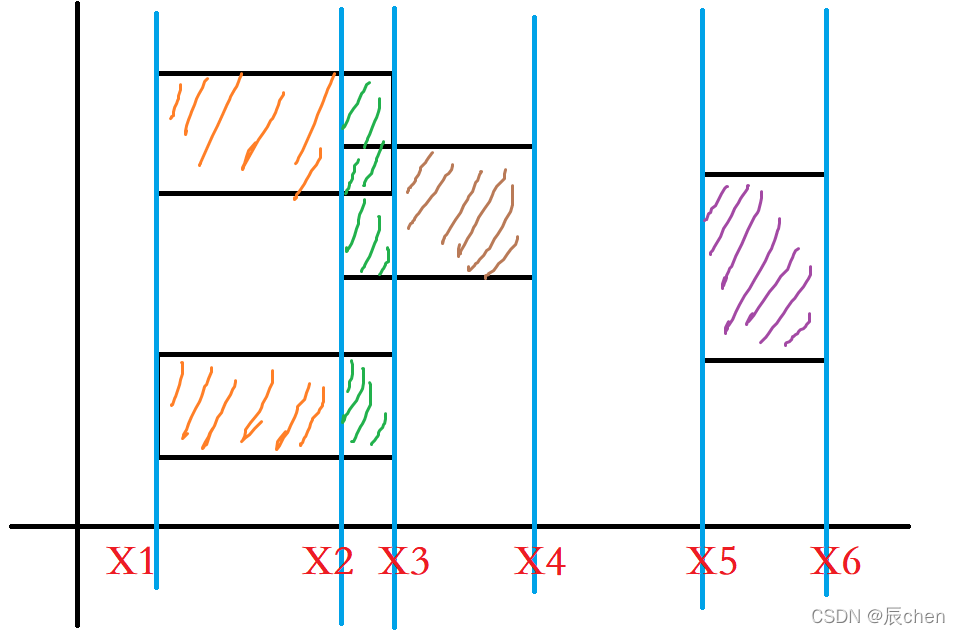
在这里插入图片描述
即我们在计算面积的时候有：

  • S 1 = ( x 2 − x 1 ) × l e n 1 S_1=(x_2-x_1)\times len_1 S1​=(x2​−x1​)×len1​
  • S 2 = ( x 3 − x 2 ) × l e n 2 S_2=(x_3-x_2)\times len_2 S2​=(x3​−x2​)×len2​
  • S 3 = ( x 4 − x 3 ) × l e n 3 S_3=(x_4-x_3)\times len_3 S3​=(x4​−x3​)×len3​
  • S 4 = ( x 6 − x 5 ) × l e n 4 S_4=(x_6-x_5)\times len_4 S4​=(x6​−x5​)×len4​

其中各个 l e n len len 就是被围住的矩阵的有效宽的和

每个柱形区域的面积就是这个长条的宽度 × 阴影部分高度

这样巧妙地用阴影部分的高度就解决了多个矩形相互覆盖的问题。

那么现在的问题就变成了：如何快速统计出来每个区间内部阴影部分的高度 h h h ？
这就需要用到一个非常特殊的线段树了，之所以称之为“非常特殊”是因为这个做法比较难扩展，只适用于这一类题型。

线段树中的每个结点 s t r u c t N o d e struct Node structNode 除了存储左右边间 l , r l, r l,r，
还要存储一个 c n t cnt cnt ,表示当前区间被覆盖的次数，
还有一个 l e n len len，表示至少被覆盖一次的区间的总长度。
另外，扫描线题型会用到懒标记延迟更新的思想，然后这类题型特殊的地方就是它的懒标记不更新，即不往下传（懒标记是 p u s h d o w n pushdown pushdown 操作，用父结点的信息更新子节点的信息）。

那么我们现在再看一下它的每个标记真实的含义是什么，以及它的每个子节点的信息有什么特点。
c n t 、 l e n cnt、len cnt、len标记存的是在不考虑父结点信息情况下的结果。
这两个标记不考虑上面的父结点信息，只考虑下面的子节点信息，这就是扫描线的特殊之处。

操作步骤：

首先把每个矩形的左右两个边拿出来，变成一个三元组。（线段树维护的是纵坐标，把每个矩形的竖边看成一个带权值的线段）

  • 第一个操作是给 [ y 1 , y 2 ] + 1 [y_1,y_2]+1 [y1​,y2​]+1,表示这个矩形已经过来了（想象一下，竖线是扫描线，固定不动，一个个矩形从右向左飘过来）

  • 第二个操作是给 [ y 1 , y 2 ] − 1 [y_1,y_2]-1 [y1​,y2​]−1，表示这个矩形已经全部穿过扫描线离开了。

有了这两个操作后，我们每次想统计两个相邻竖边内被阴影部分覆盖的总高度怎么办呢？
这个高度其实就是根结点的 l e n len len 的值。

说的再详细一点，我们规定，每个矩形的左竖边权值为 + 1 +1 +1，右竖边权值为 − 1 -1 −1，每次经过扫描线时，扫描线上的 c n t cnt cnt 会加上或减去经过它的矩形的竖边的权值，所以在算每两个竖线之间阴影部分面积时，阴影部分的高度就是扫描线上此时的len，而扫描线上的 l e n len len 其实就是根结点的 l e n len len，我们只算扫描线 c n t cnt cnt 大于 0 0 0 的时候的情况（实际上扫描线也不存在 c n t cnt cnt 为负的情况，因为每次 c n t cnt cnt 减 1 1 1 的时候之前已经必然加过 1 1 1，当所有矩形都离开扫描线后，扫描线 c n t cnt cnt 一定为 0 0 0，所以扫描线只有 c n t cnt cnt 为大于 0 0 0 和等于 0 0 0 的情况），也即，只有在扫描线上的 c n t cnt cnt 大于 0 0 0，说明这段区间上有阴影部分，我们才会继续计算。

小细节：线段树在本题中维护的是一段区间，这就需要把结点与区间对应起来
例如，结点 y 1 y_1 y1​ 对应的区间为 [ y 1 , y 2 − 1 ] [y_1,y_2−1] [y1​,y2​−1]

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10010;

int n;
struct Segment
{
    int x, y1, y2;
    int k;
    bool operator< (const Segment &t)const
    {
        return x < t.x;
    }
}seg[N * 2];
struct Node
{
    int l, r;
    int cnt, len;
}tr[N * 4];

void pushup(int u)
{
    if (tr[u].cnt > 0) tr[u].len = tr[u].r - tr[u].l + 1;
    else if (tr[u].l == tr[u].r) tr[u].len = 0;
    else tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}

void build(int u, int l, int r)
{
    tr[u] = {l, r};
    if (l == r) return;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}

void modify(int u, int l, int r, int k)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        tr[u].cnt += k;
        pushup(u);
    }
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, k);
        if (r > mid) modify(u << 1 | 1, l, r, k);
        pushup(u);
    }
}

int main()
{
    scanf("%d", &n);
    int m = 0;
    for (int i = 0; i < n; i ++ )
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        seg[m ++ ] = {x1, y1, y2, 1};
        seg[m ++ ] = {x2, y1, y2, -1};
    }

    sort(seg, seg + m);

    build(1, 0, 10000);

    int res = 0;
    for (int i = 0; i < m; i ++ )
    {
        if (i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x);
        modify(1, seg[i].y1, seg[i].y2 - 1, seg[i].k);
    }

    printf("%d\n", res);

    return 0;
}

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    • 
  
  • 56
    • 
  
  • 57
    • 
  
  • 58
    • 
  
  • 59
    • 
  
  • 60
    • 
  
  • 61
    • 
  
  • 62
    • 
  
  • 63
    • 
  
  • 64
    • 
  
  • 65
    • 
  
  • 66
    • 
  
  • 67
    • 
  
  • 68
    • 
  
  • 69
    • 
  
  • 70
    • 
  
  • 71
    • 
  
  • 72
    • 
  
  • 73
    • 
  
  • 74
    • 
  
  • 75
    • 
  
  • 76
    • 
  
  • 77
    • 
  
  • 78
    • 
  
  • 79
    • 
  
  • 80
    • 
  
  • 81
    • 
  
  • 82
    • 
  
  • 83
    •

文章来源: chen-ac.blog.csdn.net，作者：辰chen，版权归原作者所有，如需转载，请联系作者。

原文链接：chen-ac.blog.csdn.net/article/details/122793801

【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
数据结构
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入