神经网络与深度学习笔记(六)L2正则化
前言
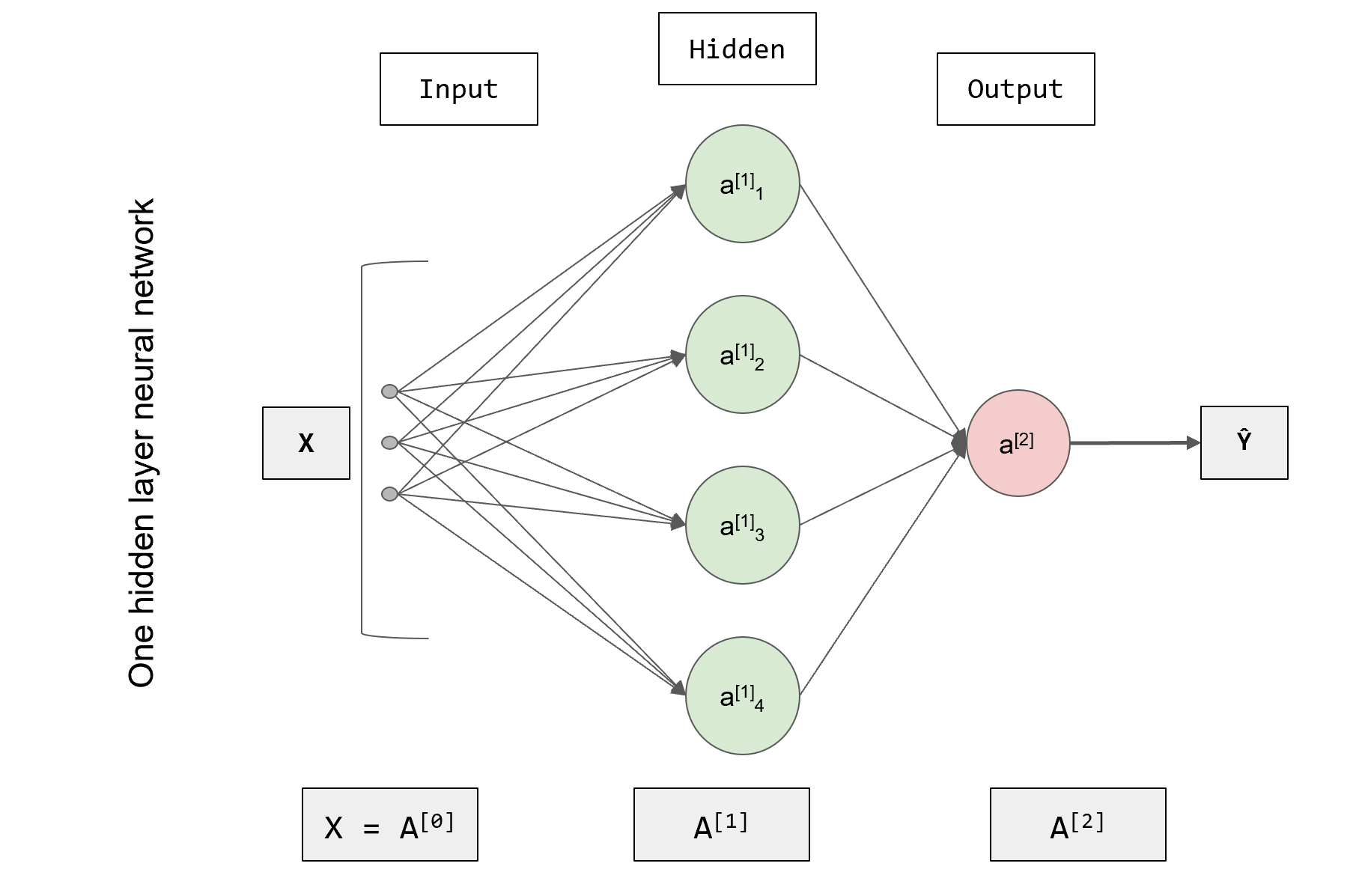
前面提到过高方差问题主要的两种方式:
- 获取更多的数据去训练。然而这种方式局限在于,数据并不是总是很容易获得的或者数据获取的代价很大。
- 正则化。这就是这篇文章需要来讨论的主题。
最小化代价函数正则化
使用 L 2 L_2 L2 正则化的最小化代价函数:
m i n ( w , b ) ȷ ( w , b ) = 1 m ∑ i = 1 m ȷ ( y ^ ( i ) , y ( i ) ) + λ 2 m ∣ ∣ w ∣ ∣ 2 2 min_{(w,b)} \jmath(w,b) = \frac{1}{m}\sum_{i=1}^m\jmath(\hat y^{(i)},y^{(i)}) + \frac{\lambda}{2m} \lvert \lvert w\lvert \lvert^{2}_{2} min(w,b)ȷ(w,b)=m1i=1∑mȷ(y^(i),y(i))+2mλ∣∣w∣∣22
其中, λ \lambda λ 称为正则化参数。在编程过程中,常常把 λ \lambda λ 写为lambd,以防止和Python语言中的关键字lamba起冲突。这一参数通常需要调优,使用开发集或者交叉验证集来验证。
那么:
∣ ∣ w ∣ ∣ 2 2 \lvert \lvert w\lvert\lvert^{2}_{2} ∣∣w∣∣22
到底是啥意思?
实际上, ∣ w ∣ 2 2 \lvert w\lvert^{2}_{2} ∣w∣22 被称为 L 2 L_{2} L2 正则化,又称为参数 w w w 的欧几里得范数, L 2 L_2 L2 范数等
∣ ∣ w ∣ ∣ 2 2 = ∑ j = 1 n x w j 2 = w T w \lvert\lvert w \lvert \lvert^{2}_{2} = \sum_{j=1}^{n_x}w_j^{2}=w^Tw ∣∣w∣∣22=j=1∑nxwj2=wTw
既然有 L 2 L_2 L2 范数,那么 L 1 L_1 L1 范数是啥?
L 1 L_1 L1 范数即为:
∣ ∣ w ∣ ∣ 1 = ∣ w 1 ∣ + ∣ w 2 ∣ + ∣ w 3 ∣ + ⋯ ∣ w n ∣ \lvert\lvert w \lvert\lvert_{1} = \lvert w_1\lvert + \lvert w_2\lvert + \lvert w_3\lvert + \cdots \lvert w_n\lvert ∣∣w∣∣1=∣w1∣+∣w2∣+∣w3∣+⋯∣wn∣
与此对应的 L 1 L_1 L1 正则化
∑ j = 1 n x ∣ w j ∣ = ∣ ∣ w ∣ ∣ 1 \sum_{j=1}^{n_x} \lvert w_j\lvert = \lvert\lvert w\lvert\lvert_{1} j=1∑nx∣wj∣=∣∣w∣∣1
使用 L 1 L_1 L1 正则化的最小代价函数为:
m i n ( w , b ) ȷ ( w , b ) = 1 m ∑ i = 1 m ȷ ( y ^ ( i ) , y ( i ) ) + λ 2 m ∣ ∣ w ∣ ∣ 1 min_{(w,b)} \jmath(w,b) = \frac{1}{m}\sum_{i=1}^m\jmath(\hat y^{(i)},y^{(i)}) + \frac{\lambda}{2m} \lvert \lvert w\lvert\lvert_{1} min(w,b)ȷ(w,b)=m1i=1∑mȷ(y^(i),y(i))+2mλ∣∣w∣∣1
然而使用 L 1 L_1 L1 正则化的效果并不是太明显,主要是因为使用后会导致 w w w 稀疏, w w w 矢量中会有很多 0,虽然模型会有一定的压缩但是效果不大。
这就是为什么通常使用 L 2 L_2 L2 正则化而不是 L 1 L_1 L1 正则化的原因。
那么, b b b 参数是否可以正则化呢?比如: λ 2 m b 2 \frac{\lambda}{2m}b^2 2mλb2
答案也是效果不大。
因为参数实际上大多数集中在 w w w 中,而不是 b b b ,即使对 b b b 进行了正则化, b b b 对模型的影响效果也不是太大
在神经网络中的 L 2 L_2 L2 正则化
ȷ ( w [ 1 ] , b [ 1 ] , ⋯ w [ l ] , b [ l ] ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) + λ 2 m ∑ i = 1 l ∣ ∣ w [ l ] ∣ ∣ 2 ∣ ∣ w [ l ] ∣ ∣ 2 = ∑ i = 1 n [ l ] ∑ j = 1 n [ l − 1 ] ( w i j [ l ] ) 2 w [ l ] : ( n [ l ] , n [ l − 1 ] ) \jmath (w^{[1]},b^{[1]},\cdots w^{[l]},b^{[l]}) = \frac{1}{m} \sum_{i=1}^{m}L(\hat y^{(i)},y^{(i)})+\frac{\lambda}{2m}\sum_{i=1}^l \lvert \lvert w^{[l]} \lvert\lvert^{2}\\ \lvert \lvert w^{[l]} \lvert \lvert^{2} = \sum_{i = 1}^{n^{[l]}} \sum_{j=1}^{n^{[l-1]}}(w_{ij}^{[l]})^2 \\ w^{[l]}:(n^{[l]},n^{[l-1]})\\ ȷ(w[1],b[1],⋯w[l],b[l])=m1i=1∑mL(y^(i),y(i))+2mλi=1∑l∣∣w[l]∣∣2∣∣w[l]∣∣2=i=1∑n[l]j=1∑n[l−1](wij[l])2w[l]:(n[l],n[l−1])
其中矩阵的 ∣ ∣ w [ l ] ∣ ∣ 2 = ∑ i = 1 n [ l ] ∑ j = 1 n [ l − 1 ] ( w i j [ l ] ) 2 \lvert \lvert w^{[l]} \lvert \lvert^{2} = \sum_{i = 1}^{n^{[l]}} \sum_{j=1}^{n^{[l-1]}}(w_{ij}^{[l]})^2 ∣∣w[l]∣∣2=∑i=1n[l]∑j=1n[l−1](wij[l])2 ,表示矩阵中元素平方和。又称为弗罗贝尼乌斯范数(Frobenius norm) ,这里就不叫 L 2 L_2 L2 范数了。(为啥?我也不知道,而且弗罗贝尼乌斯范数不是对应元素的平方和再开方嘛?为什么这里不开方?)
在梯度下降的过程中, d w [ l ] dw^{[l]} dw[l], w [ l ] w^{[l]} w[l]也会变化
d w [ l ] = d z [ l ] ∗ a [ l − 1 ] + λ m w [ l ] w [ l ] = w [ l ] − α d w [ l ] = w [ l ] − α ∗ ( d z [ l ] ∗ a [ l − 1 ] + λ m w [ l ] ) = w [ l ] − α λ m w [ l ] − α ( d z [ l ] ∗ a [ l − 1 ] ) = w [ l ] ( 1 − α λ m ) − α ( d z [ l ] ∗ a [ l − 1 ] ) dw^{[l]} = dz^{[l]} * a^{[l-1]} + \frac{\lambda}{m}w^{[l]}\\ w^{[l]} = w^{[l]} - \alpha dw^{[l]}\\ = w^{[l]} - \alpha *(dz^{[l]} * a^{[l-1]} + \frac{\lambda}{m}w^{[l]})\\ = w^{[l]} -\frac{\alpha \lambda}{m}w^{[l]} - \alpha(dz^{[l]} * a^{[l-1]})\\ = w^{[l]}(1-\frac{\alpha \lambda}{m}) - \alpha(dz^{[l]} * a^{[l-1]})\\ dw[l]=dz[l]∗a[l−1]+mλw[l]w[l]=w[l]−αdw[l]=w[l]−α∗(dz[l]∗a[l−1]+mλw[l])=w[l]−mαλw[l]−α(dz[l]∗a[l−1])=w[l](1−mαλ)−α(dz[l]∗a[l−1])
故,在梯度下降过程中, w w w 是逐渐变小的,所以 L 2 L_2 L2 正则化有时称之为权重衰减
为什么 L 2 L_2 L2 正则化可以防止过拟合,减少方差?
ȷ ( w [ 1 ] , b [ 1 ] , ⋯ w [ l ] , b [ l ] ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) + λ 2 m ∑ i = 1 l ∣ ∣ w [ l ] ∣ ∣ 2 \jmath (w^{[1]},b^{[1]},\cdots w^{[l]},b^{[l]}) = \frac{1}{m} \sum_{i=1}^{m}L(\hat y^{(i)},y^{(i)})+\frac{\lambda}{2m}\sum_{i=1}^l \lvert \lvert w^{[l]} \lvert \lvert^{2}\\ ȷ(w[1],b[1],⋯w[l],b[l])=m1i=1∑mL(y^(i),y(i))+2mλi=1∑l∣∣w[l]∣∣2
观察上图的公式:
当 λ ↑ \lambda \uparrow λ↑ 且 λ \lambda λ 足够大的时候 ——> w w w 就会 → 0 \rightarrow 0 →0 ——> 从而将隐藏单元的影响削减 ——> 进一步使得神经网络简单化 ——> 最终使得神经网络接近逻辑回归
举个例子:
当激活函数是 t a n h ( z ) tanh(z) tanh(z) 时,
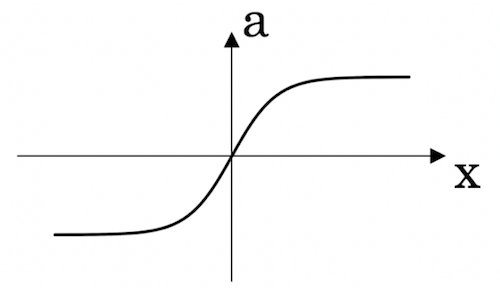
λ ↑ ⟶ w [ l ] ↓ ⟶ ( z [ l ] = w [ l ] a [ l − 1 ] + b [ l ] ) ↓ ⟶ 接 近 线 性 \lambda \uparrow \longrightarrow w^{[l]} \downarrow \longrightarrow (z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]})\downarrow \longrightarrow 接近线性 λ↑⟶w[l]↓⟶(z[l]=w[l]a[l−1]+b[l])↓⟶接近线性
因为 w [ l ] w^{[l]} w[l] 变小会导致以 w [ l ] w^{[l]} w[l] 为参数求出的 z [ l ] z^{[l]} z[l] 的值变小,使得隐藏单元的影响削减,使得神经网络简单化,最后使得神经网络接近逻辑回归
就降低了方差
同时,在使用 L 2 L_2 L2正则化时建议画出 ȷ \jmath ȷ 关于梯度下降迭代次数的图像
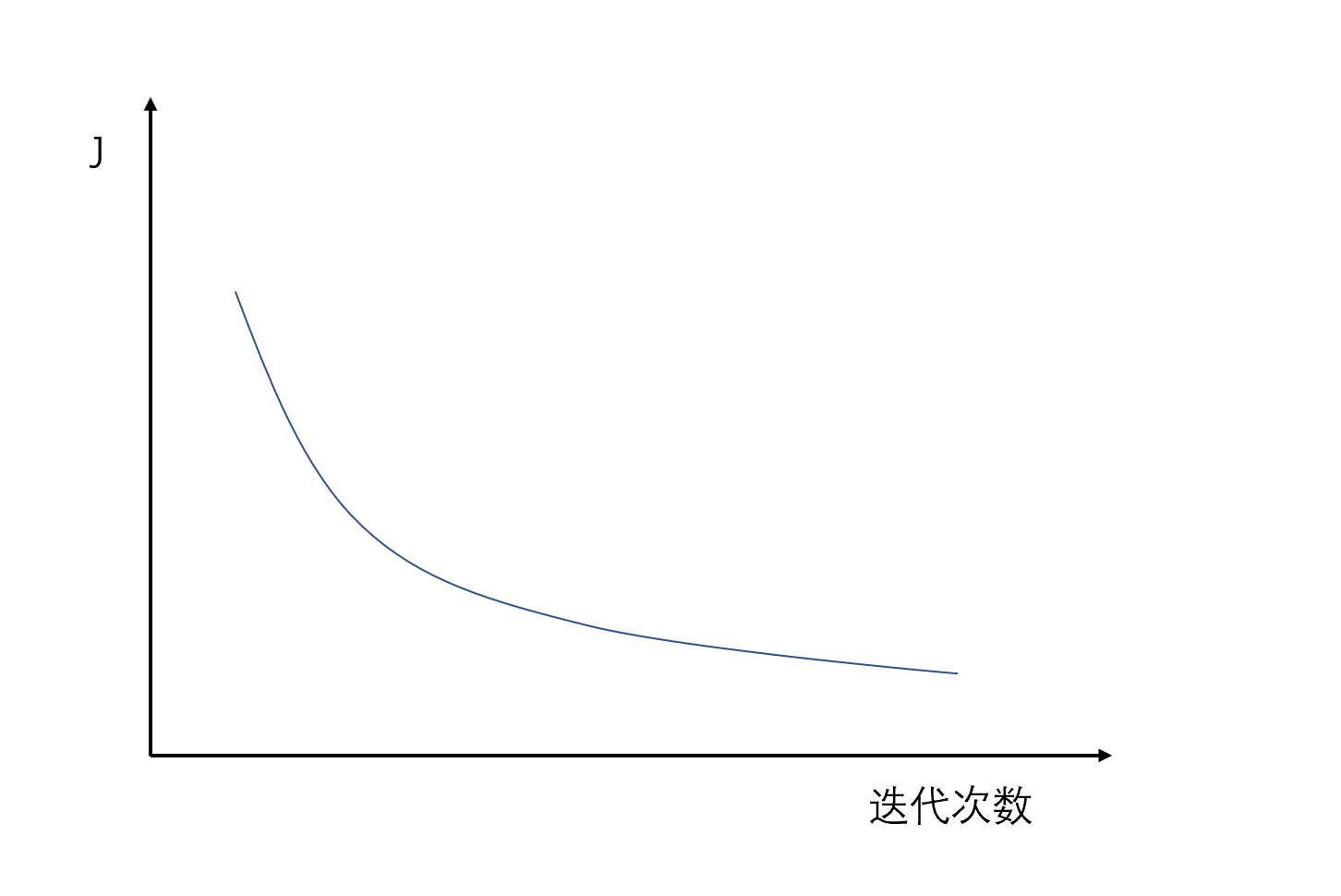
你会发现使用 L 2 L_2 L2 正则化后,随着迭代次数的增加, ȷ \jmath ȷ 的值会逐渐减小
文章来源: blog.csdn.net,作者:沧夜2021,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/CANGYE0504/article/details/118607882
- 点赞
- 收藏
- 关注作者


评论(0)