基于PaddlePaddle的LeNet神经网络MNIST数据集分类

举报
陈沧夜 发表于 2022/04/29 23:07:22 2022/04/29
【摘要】 文章目录 1.前言2.算法设计2.1任务流程2.2 LeNet简述2.3 算法设计2.3.1 引入相关的包2.3.2 读取数据集2.3.3 归一化数据集2.3.4 取出一个数据瞅瞅2.3.5 定义...

文章目录

1.前言

MNIST是一个手写体数字的图片数据集，MNIST是深度学习领域标准、易用的成熟数据集，该数据集来由美国国家标准与技术研究所（National Institute of Standards and Technology (NIST)）发起整理，一共统计了来自250个不同的人手写数字图片，其中50%是高中生，50%来自人口普查局的工作人员。该数据集的收集目的是希望通过算法，实现对手写数字的识别。


MNIST


1998年，Yan LeCun 等人发表了论文《Gradient-Based LearningApplied to Document Recognition》，首次提出了LeNet-5 网络，利用上述数据集实现了手写字体的识别。

Mnist数据集官网：http://yann.lecun.com/exdb/mnist/

在上述文件中，训练集一共包含了 60,000 张图像和标签，而测试集一共包含了 10,000 张图像和标签。测试集中前5000个来自最初NIST项目的训练集，后5000个来自最初NIST项目的测试集。前5000个比后5000个要规整，这是因为前5000个数据来自于美国人口普查局的员工，而后5000个来自于大学生。

如今在深度学习领域，卷积神经网络占据了至关重要的地位，从最早LeCun提出的简单LeNet，到如今ImageNet大赛上的优胜模型VGGNet、GoogLeNet、ResNet等，人们在图像分类领域，利用卷积神经网络得到了一系列惊人的结果。

2.算法设计

2.1任务流程

本次使用飞桨框架来完成手写数字识别模型任务，其预测模型任务的流程为：


任务流程


数据处理：从本地或者URL读取数据，并完成预处理操作（如数据校验，格式转化等），保证模型可读取。

模型设计：网络结构设计，相当于模型的假设空间，即模型能够表达的关系集合。

训练配置：设定模型采用带寻解算法，即优化器，并指定计算资源。

训练过程：循环调用训练过程，每轮都包括前向计算，损失函数（优化目标）和反向传播三个步骤。

模型保存：将训练好的模型保存，模型预测时调用。

2.2 LeNet简述

LeNet是一种用于手写体字符识别的非常高效的卷积神经网络。

出自论文《Gradient-Based Learning Applied to Document Recognition》

由深度学习三巨头之一的Yan LeCun提出，他同时也是卷积神经网络CNN之父

LeNet主要用来进行手写字符的识别与分类，并在美国的银行中投入了使用。

其实现确立了CNN的结构，现在神经网络中的许多内容在LeNet的网络结构中都能看到。


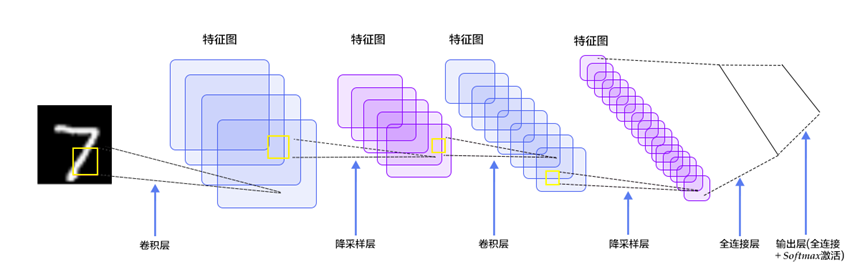
结构图

2.3 算法设计

# 打印飞桨版本
import paddle
print(paddle.__version__)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    •

2.3.1 引入相关的包

from paddle.vision.transforms import Compose, Normalize
import numpy as np
import matplotlib.pyplot as plt
import paddle
import paddle.nn.functional as F
from paddle.metric import Accuracy

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    •

2.3.2 读取数据集

手写数字的MNIST数据集，包含60,000个用于训练的示例和10,000个用于测试的示例。这些数字已经过尺寸标准化并位于图像中心，图像是固定大小(28x28像素)，其值为0到1。

飞桨提供了多个封装好的数据集API，涵盖计算机视觉、自然语言处理、推荐系统等多个领域，帮助开发者快速完成深度学习任务。

如在手写数字识别任务中，通过paddle.vision.datasets.MNIST可以直接获取处理好的MNIST训练集、测试集.

飞桨API支持如下常见的学术数据集：

  1. mnist
  2. cifar
  3. Conll05
  4. Imdb
  5. Imikolov
  6. Movielens
  7. Sentiment
  8. uci_housing
  9. wmt14
  10. wmt16

通过paddle.vision.datasets.MNIST API设置数据读取器，代码如下所示。

train_dataset = paddle.vision.datasets.MNIST(mode='train', transform=transform)
test_dataset = paddle.vision.datasets.MNIST(mode='test', transform=transform)

  
 
    
  
  • 1
    • 
  
  • 2
    •

2.3.3 归一化数据集

使用paddle.vision.transforms.Normalize 对图像进行归一化。

图像归一化处理支持两种方式：

  1. 用统一的均值和标准差值对图像的每个通道进行归一化处理；
  2. 对每个通道指定不同的均值和标准差值进行归一化处理。
    计算过程：output[channel] = (input[channel] - mean[channel]) / std[channel]

以下代码实现了数据集归一化的过程。

transform = Compose([Normalize(mean=[127.5],
                               std=[127.5],
                               data_format='CHW')])

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    •

mean ()中填入用于每个通道归一化的均值。

std () 用于每个通道归一化的标准差值。

to_rgb (bool, optional) - 是否转换为 rgb 的格式。默认值：False。

transform = Compose([Normalize(mean=[127.5],
                               std=[127.5],
                               data_format='CHW')])
# 使用transform对数据集做归一化
print('download training data and load training data')
train_dataset = paddle.vision.datasets.MNIST(mode='train', transform=transform)
test_dataset = paddle.vision.datasets.MNIST(mode='test', transform=transform)
print('load finished')


  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    •

2.3.4 取出一个数据瞅瞅

train_data0, train_label_0 = train_dataset[0][0],train_dataset[0][1]
train_data0 = train_data0.reshape([28,28])
plt.figure(figsize=(2,2))
plt.imshow(train_data0, cmap=plt.cm.binary)
print('train_data0 label is: ' + str(train_label_0))
print("图像数据形状和对应数据为:", train_data0.shape)
print("图像标签形状和对应数据为:", train_label_0.shape, train_label_0)
print("\n打印第一个batch的第一个图像，对应标签数字为{}".format(train_label_0))
#print(train_data0)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    •

2.3.5 定义LeNet网络

paddle.nn 文档目录下包含飞桨框架支持的神经网络层和相关函数的相关API
本次使用paddle.nn下的Conv2D、MaxPool2D、Linear等完成LeNet的构建。

class LeNet(paddle.nn.Layer):
    def __init__(self):
        super(LeNet, self).__init__()
        # 定义卷积层，输出特征通道in_channels设置为1，out_channels设置为6，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
        self.conv1 = paddle.nn.Conv2D(in_channels=1, out_channels=6, kernel_size=5, stride=1, padding=2)
        # 定义池化层，池化核的大小kernel_size为2，池化步长为2
        self.max_pool1 = paddle.nn.MaxPool2D(kernel_size=2,  stride=2)
        # 定义卷积层，输出特征通道in_channels设置为6，out_channels设置为16，卷积核的大小kernel_size为5，卷积步长stride=1
        self.conv2 = paddle.nn.Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1)
        # 定义池化层，池化核的大小kernel_size为2，池化步长为2
        self.max_pool2 = paddle.nn.MaxPool2D(kernel_size=2, stride=2)
        # 定义一层全连接层，输入维度16*5*5，输出维度是120
        self.linear1 = paddle.nn.Linear(in_features=16*5*5, out_features=120)
        # 定义一层全连接层，输入维度120，输出维度是84
        self.linear2 = paddle.nn.Linear(in_features=120, out_features=84)
        # 定义一层全连接层，输入维度84，输出维度是10
        self.linear3 = paddle.nn.Linear(in_features=84, out_features=10)

    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.max_pool1(x)
        x = self.conv2(x)
        x = F.relu(x)
        x = self.max_pool2(x)
        x = paddle.flatten(x, start_axis=1,stop_axis=-1)
        x = self.linear1(x)
        x = F.relu(x)
        x = self.linear2(x)
        x = F.relu(x)
        x = self.linear3(x)
        return x


  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    •

2.3.6 封装模型并配置

2.3.6.1 Adam优化器

Adam优化器可以在paddle.optimizer.Adam中定义

Adam优化器出自Adam论文的第二节，能够利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。

其参数更新的计算公式如下：

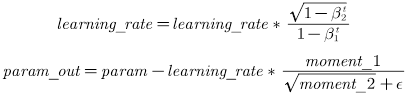
论文链接：https://arxiv.org/abs/1412.6980

在优化器中可以自定义学习率learning_rate ()，用于参数更新的计算。可以是一个浮点型值或者一个_LRScheduler类，默认值为0.001。

2.3.6.2 损失函数

损失函数使用交叉熵损失函数CrossEntropyLoss()，计算输入input和标签label间的交叉熵损失 ，它结合了 LogSoftmax和NLLLoss 的OP计算，可用于训练一个n类分类器。

如果提供 weight 参数的话，它是一个 1-D 的tensor, 每个值对应每个类别的权重。

该损失函数的数学计算公式如下：

当 weight 不为 none 时，损失函数的数学计算公式为：

2.3.6.3 精确度

使用 paddle.metric.Accuracy() 计算精确度。

model = paddle.Model(LeNet())   # 用Model封装模型
optim = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters())

# 配置模型
model.prepare(
    optim,
    paddle.nn.CrossEntropyLoss(),
    Accuracy()
    )


  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    •

2.3.7 训练模型

使用model.fit进行模型训练

下面的代码中可以定义epochs和batch_size等。

Verbosre = 1表示使用进度条的方式打印日志。

# 训练模型
model.fit(train_dataset,
        epochs=2,
        batch_size=64,
        verbose=1
        )


  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    •

2.3.8 使用模型预测

model.evaluate(test_dataset, batch_size=64, verbose=1)


  
 
    
  
  • 1
    • 
  
  • 2
    •

2.4 不同参数对预测精度的影响

本次探究learning_rate,epochs,batch_size三个参数对预测精度的影响

2.4.1 重新封装模型

重新封装模型使得可以传入参数learning_rate,epochs,batch_size

def MLtest(learning_rate,epochs,batch_size):
    print("======start=========")
    print("this learningrate is--->",learning_rate)
    print("this epochs       is--->",epochs)
    print("this batch_size   is--->",batch_size)

    model = paddle.Model(LeNet())   # 用Model封装模型
    optim = paddle.optimizer.Adam(learning_rate=learning_rate, parameters=model.parameters())
    # 配置模型
    model.prepare(
        optim,
        paddle.nn.CrossEntropyLoss(),
        Accuracy()
        )
    model.fit(train_dataset,
        epochs=epochs,
        batch_size=batch_size,
        verbose=1
        )
    acc = model.evaluate(test_dataset, batch_size=64, verbose=1)
    accuracy.append(acc['acc'])
    print(acc['acc'])
    print("=======end==========")

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    •

2.4.2 学习率对预测精度的影响

learning_rate=[x*0.001 for x in range(1,20)]
accuracy = []
for i in learning_rate:
    MLtest(i,epochs=2,batch_size=64)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    •

在以上代码中，设定epochs为2,batch_size为64

learning_rate的值我们用列表生成式来生成

learning_rate=[x*0.001 for x in range(1,20)]
print(learning_rate)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
 
learning_rate=[x*0.001 for x in range(1,20)]
print(learning_rate)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
 
# 别把epochs设置太大，要不然有你跑的
learning_rate=[x*0.001 for x in range(1,20)]
accuracy = []
for i in learning_rate:
    MLtest(i,epochs=2,batch_size=64)
plt.plot(learning_rate,accuracy)
plt.xlabel('learning_rate')
plt.ylabel('accuracy')
plt.title('Influence of learning rate on prediction accuracy')
plt.show()

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    •

2.4.3 训练的轮数对预测精度的影响

epochs = [x for x in range(1,30) ]
accuracy = []
for i in epochs:
    MLtest(learning_rate=0.001,epochs=i,batch_size=64)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    •

在以上代码中，设定learning_rate为0.001,batch_size为64，epochs的值我们用列表生成式来生成

epochs = [x for x in range(1,30) ]

  
 
    
  
  • 1
    •

【警告!警告!警告!】

这一部分测试代码的运行时间应该是最长的

请务必开启至尊算力

同时做好打了好几局王者荣耀还没运行完的准备

epochs = [x for x in range(1,30) ]
print(epochs)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
 
epochs = [x for x in range(1,30) ]
accuracy = []
for i in epochs:
    MLtest(learning_rate=0.001,epochs=i,batch_size=64)
plt.plot(epochs,accuracy)
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.title('Influence of epochs on prediction accuracy')
plt.show()

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    •

2.4.4 数据的批大小对预测精度的影响

batch_size = [x for x in range(50,100)]
accuracy = []
for i in batch_size:
    MLtest(learning_rate=0.001,epochs=2,batch_size=i)

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    •

在以上代码中，设定learning_rate为0.001,epochs为2，batch_size的值我们用列表生成式来生成

batch_size = [x for x in range(50,100)]

  
 
    
  
  • 1
    • 
 
batch_size = [x for x in range(50,100)]
accuracy = []
for i in batch_size:
    MLtest(learning_rate=0.001,epochs=2,batch_size=i)
plt.plot(batch_size,accuracy)
plt.xlabel('batch_size')
plt.ylabel('accuracy')
plt.title('Influence of batch_size on prediction accuracy')
plt.show()

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    •

3. 总结

本次探究learning_rate,epochs,batch_size三个参数对预测精度的影响。

通过运行的结果可见，参数的调整是人工智能模型训练过程中较为重要的一个部分。

好的参数能够大大减少模型运行的速度，也能带来较高的精确率。

文章来源: blog.csdn.net，作者：沧夜2021，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/CANGYE0504/article/details/122737640

【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
神经网络
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入