虫子 二叉树 内核必备，基本算法，linux二次发育，项目远见

举报
虫子VV 发表于 2022/04/21 13:58:01 2022/04/21
【摘要】 链式二叉树 那么链式二叉树有什么好的地方呢 二叉树的遍历 前序、中序以及后序遍历 按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：（上图为例图）（前中后访问根的时机不一样） 分治 二叉树 二叉树节点 我们把上面的树建好 二叉树前序遍历 二叉树中序遍历 二叉树后序遍历 二叉树节点个数 次数用传址的方式 次数用返回值的方式（假如我是代码我必然要嫁给这条代码） 二叉树叶子节点个数 二叉...

链式二叉树

我们需要明白一点，就是普通的二叉树==增删查改==没有什么价值，因为普通二叉树用来存数据复杂且不方便

那么链式二叉树有什么好的地方呢

==价值体现：==在他的基础之上，增加一些性质，才有意义

1.==搜索二叉树 ：==最多查找高度次—>时间复杂度O(N)—>单链树也就引出平衡二叉树—>AVL树和红黑树

2.Huffman 树（以后再说，反正不是现在了解的）

我们不关注普通二叉树的增删查改，我们关注递归遍历结构

1.为后面学习更有用树打基础

2.很多oj题结构普遍二叉树

==二叉树被分成 根 左子树 右子树==

二叉树的遍历

前序、中序以及后序遍历

学习二叉树结构，最简单的方式就是遍历。所谓==二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。==访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

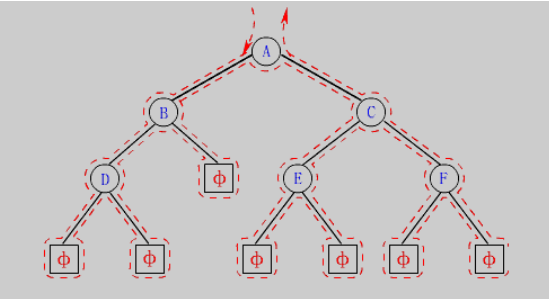
image-20211112211723351

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：（上图为例图）（前中后访问根的时机不一样）

image-20211112213707848

1.前序遍历(Preorder Traversal 亦称==先序遍历==)——访问根结点的操作发生在遍历其左右子树之前。==根 左子树 右子树==

上图前序遍历的顺序是：A B D NULL NULL NULL C E NULL NULL F NULL NULL==只有把空放进去才能真正的知道思想，那些不加 空的就是耍流氓，没错说的就是你们老师，对你们耍流氓==

2.中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。==左子树 根 右子树==

上图中序遍历的顺序是：NULL D NULL B NULL A （这时候想访问C就得访问E）NULL E NULL C NULL F NULL

3.后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。==左子树 右子树 根==

上图后序遍历的顺序是：NULL NULL D NULL B NULL NULL E NULL NULL F C A

分治

这里我们用的思想是分治的思想，分而治之-----大事化小，小事化了

二叉树

二叉树节点

//二叉树数据类型
typedef char BTDataType;
//二叉树节点
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

我们把上面的树建好

//创建树 我们不学二叉树的增删查改原因就在这，我们想要啥树自己链一个就行，没必要增删查改
BTNode* CreatBinaryTree()
{
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');
	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
	return nodeA;
}

二叉树前序遍历

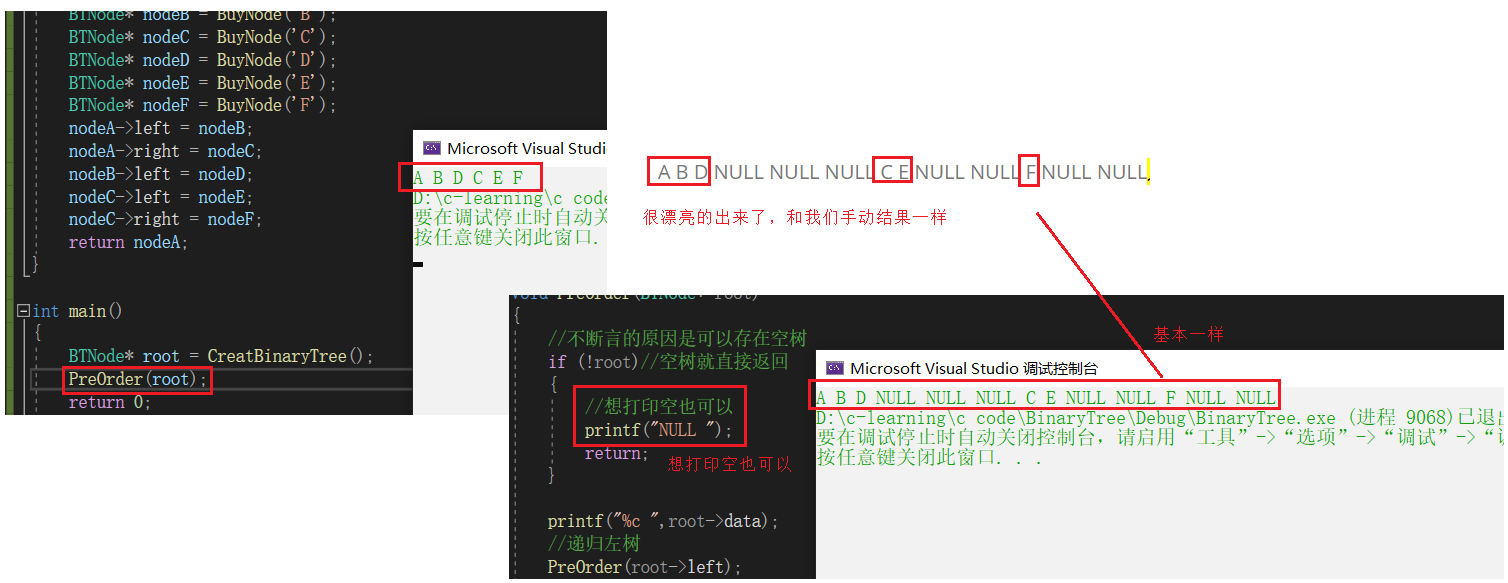
image-20211113085631295

==这张图我实际上是想通过左右与上下滚动联合操作来截图的，然后我就找几个小时，基本能找的都找了，全网没有左右滚动截图的软件基本全是截图后窗口亮，不可以操作外面的滚动条，就算能操作也不可以左右滚动截图==

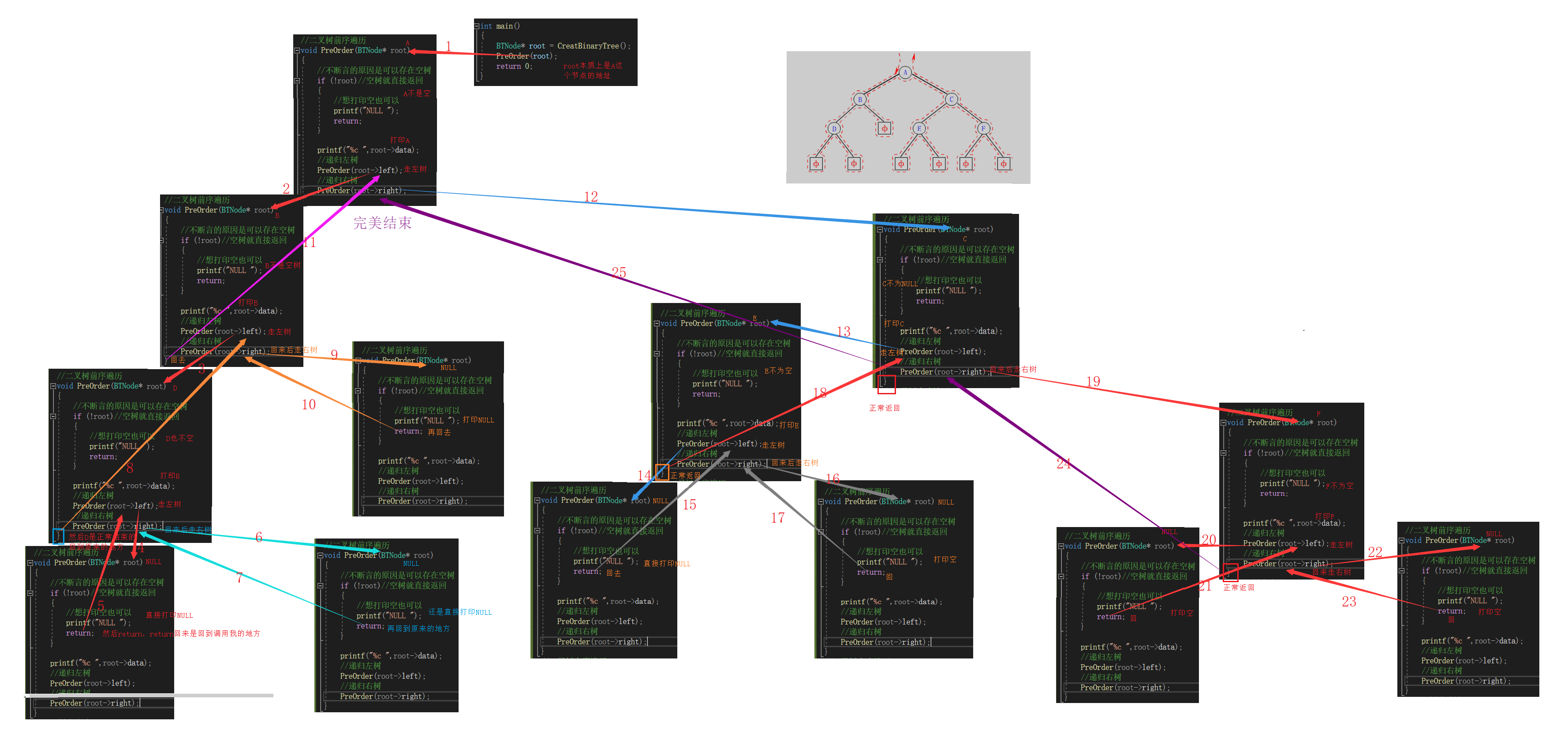
//二叉树前序遍历
void PreOrder(BTNode* root)
{
	//不断言的原因是可以存在空树
	if (!root)//空树就直接返回
	{
		return;
	}
	printf("%c ",root->data);
	//递归左树
	PreOrder(root->left);
	//递归右树
	PreOrder(root->right);
}

二叉树中序遍历

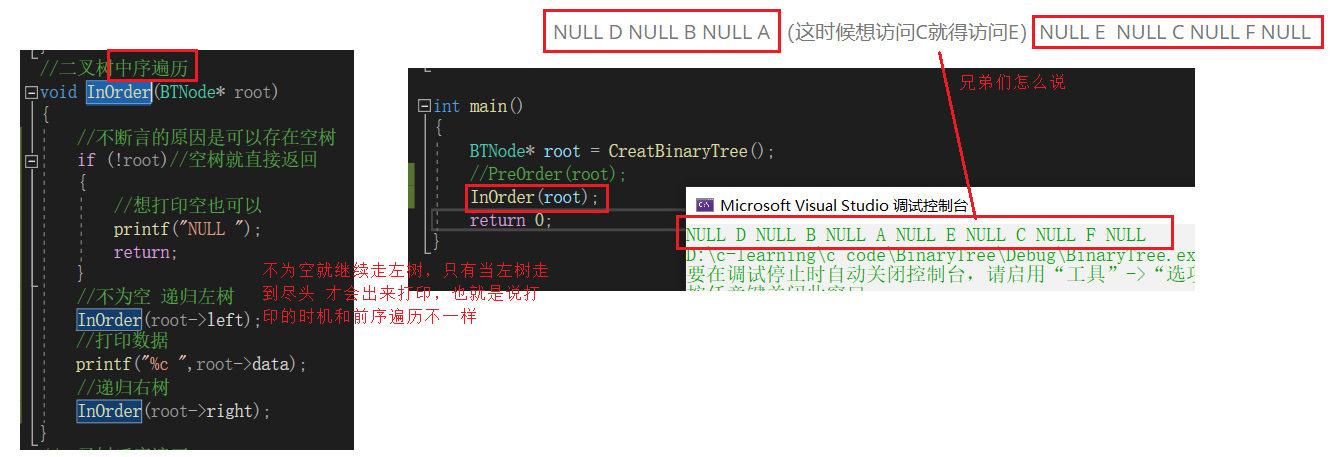
image-20211113152651694

==我故意写成一个窗口的宽度，不然会很麻烦==

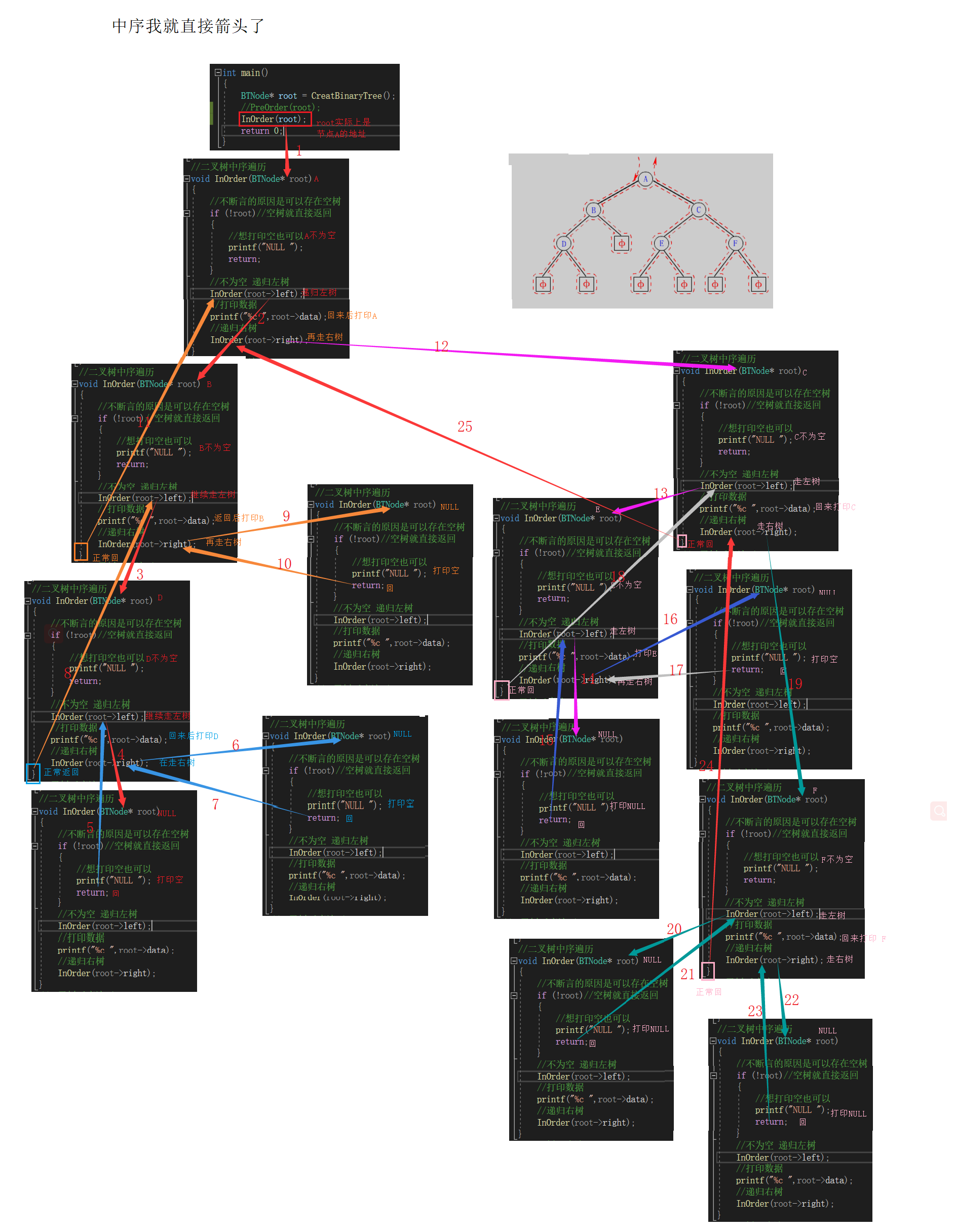
image-20211113171127588

//二叉树中序遍历
void InOrder(BTNode* root)
{
	//不断言的原因是可以存在空树
	if (!root)//空树就直接返回
	{
		//想打印空也可以
		printf("NULL ");
		return;
	}
	//不为空 递归左树
	InOrder(root->left);
	//打印数据
	printf("%c ",root->data);
	//递归右树
	InOrder(root->right);
}

二叉树后序遍历

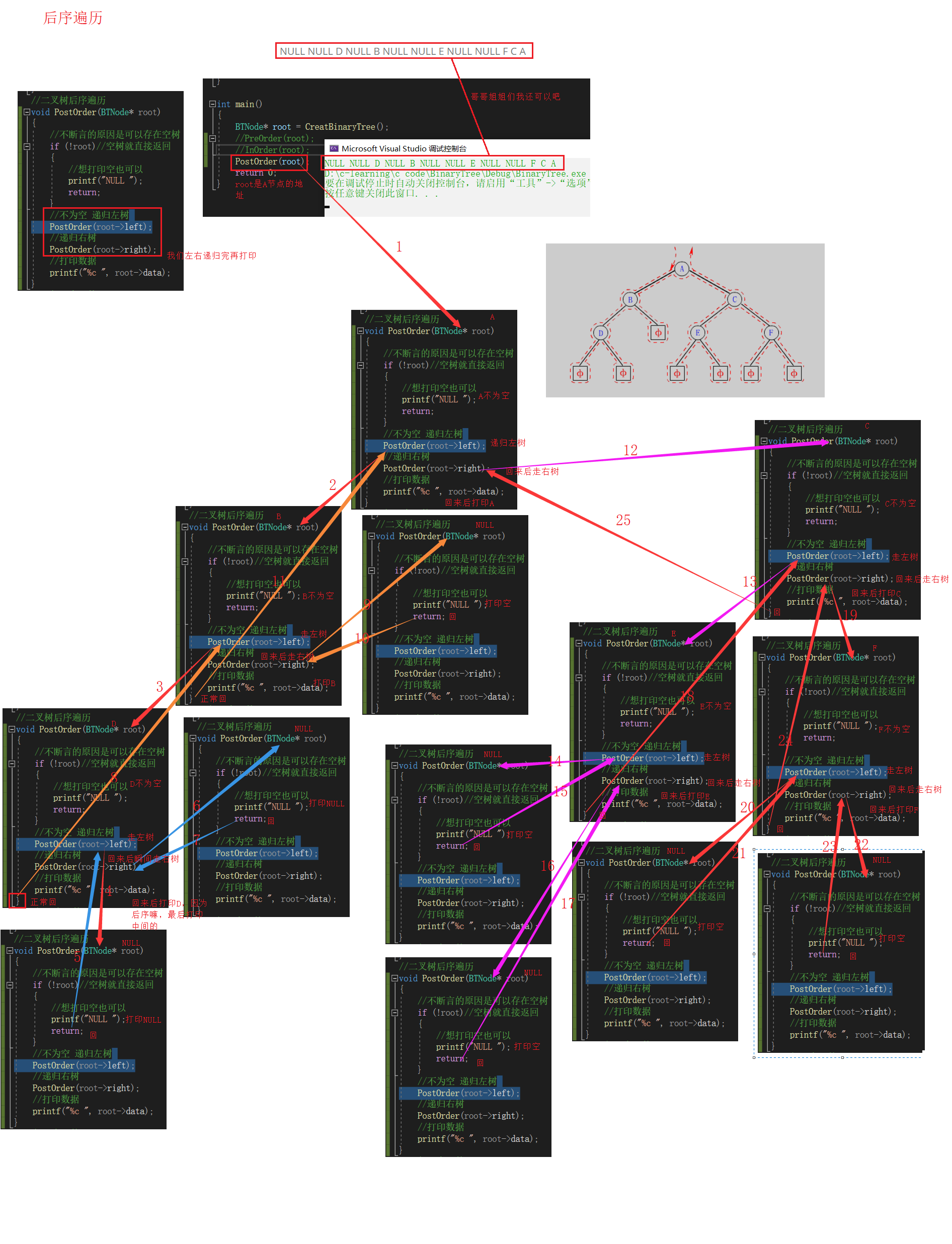
image-20211113183048915

//二叉树后序遍历
void PostOrder(BTNode* root)
{
	//不断言的原因是可以存在空树
	if (!root)//空树就直接返回
	{
		//想打印空也可以
		printf("NULL ");
		return;
	}
	//不为空 递归左树
	PostOrder(root->left);
	//递归右树
	PostOrder(root->right);
	//打印数据
	printf("%c ", root->data);
}

二叉树节点个数

次数用传址的方式

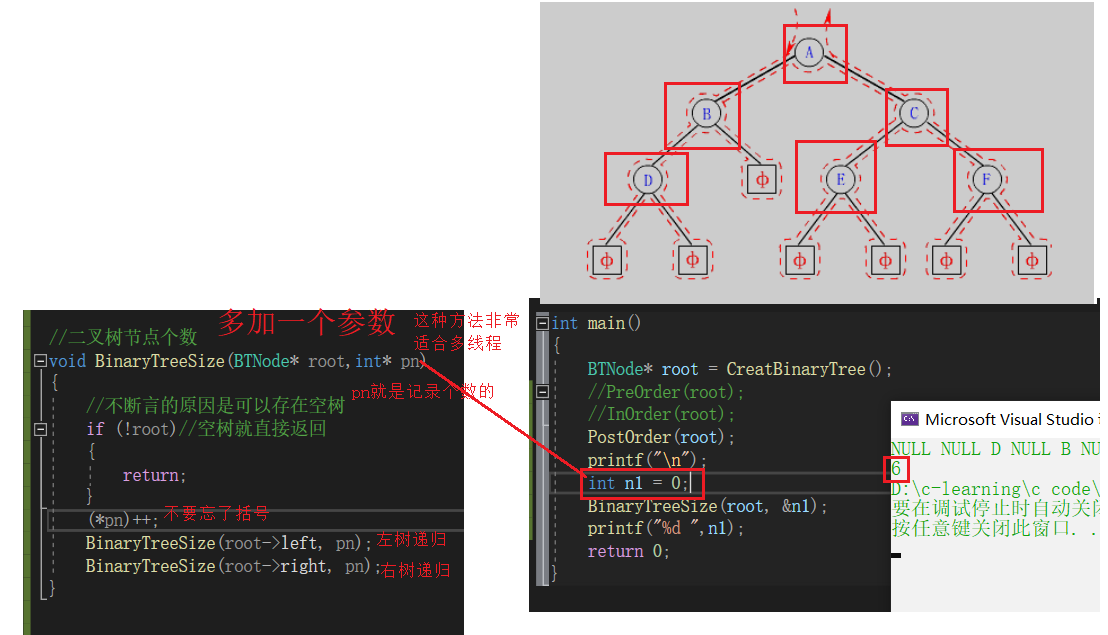
image-20211113191511501

//二叉树节点个数
void BinaryTreeSize(BTNode* root,int* pn)
{
	//不断言的原因是可以存在空树
	if (!root)//空树就直接返回
	{
		return;
	}
	(*pn)++;
	BinaryTreeSize(root->left, pn);
	BinaryTreeSize(root->right, pn);
}

次数用返回值的方式（假如我是代码我必然要嫁给这条代码）

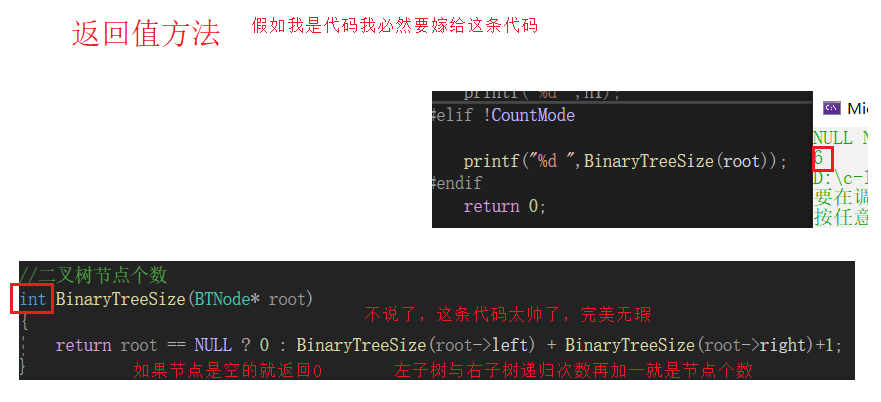
image-20211113193430719

//二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right)+1;
}

二叉树叶子节点个数

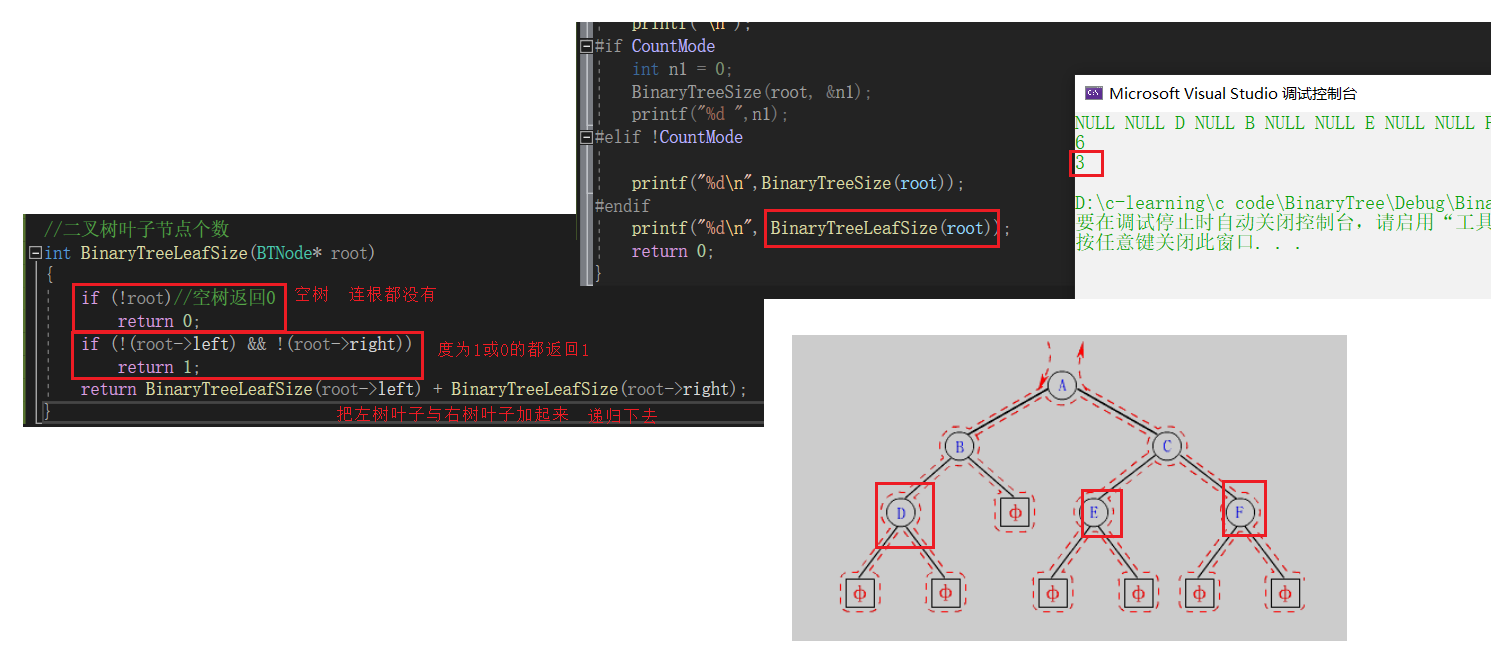
image-20211113232154579

//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (!root)//空树返回0
		return 0;
	if (!(root->left) && !(root->right))
		return 1;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

二叉树第k层节点个数

image-20211114000025087

//二叉树第k层节点个数
int BinaryTreeLevelSize(BTNode* root, int k)
{
	if (!root)
		return 0;
	if (1 == k)
		return 1;
	//root不等于空，k也不等于1，说明root这棵树的第k层节点在子树里面
	//转换成求左右子树的第k-1层节点数量
	return BinaryTreeLevelSize(root->left, k - 1) + BinaryTreeLevelSize(root->right, k - 1);
}

二叉树深度/高度

image-20211114005007897

//二叉树深度/高度
int BinaryTreeDepth(BTNode* root)
{
	if (!root)
		return 0;
	//把递归的数用变量保存起来，减少资源的消耗
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

二叉树查找值为x的节点

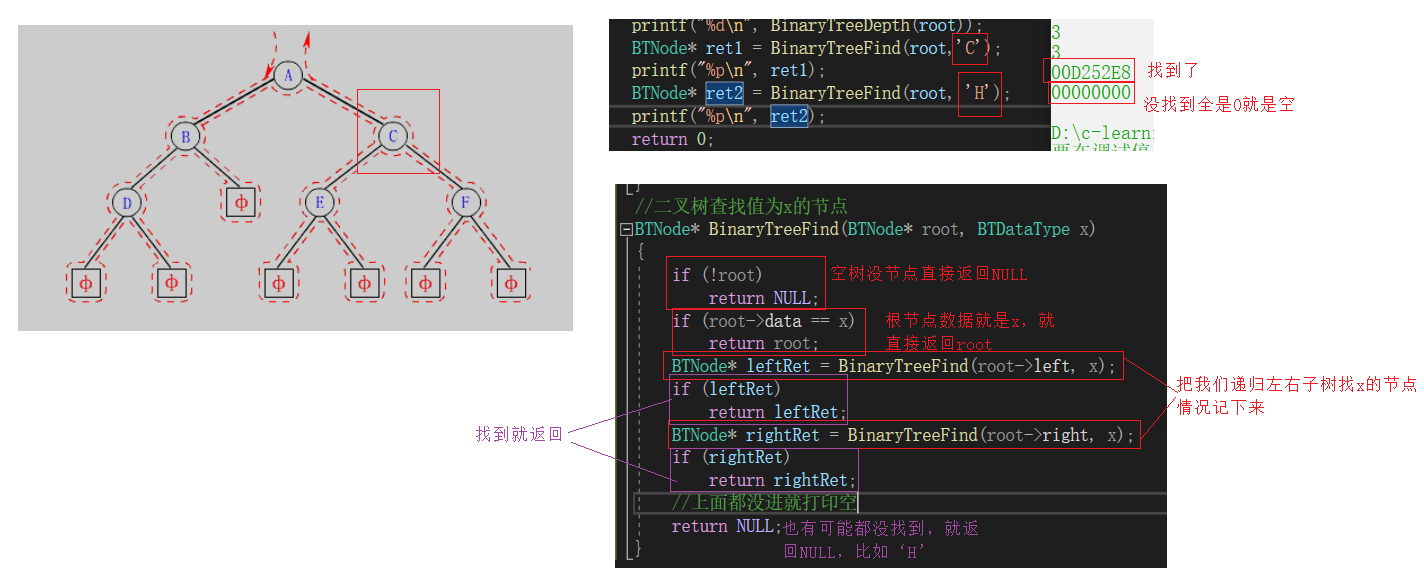
image-20211114013914115

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (!root)
		return NULL;
	if (root->data == x)
		return root;
	BTNode* leftRet = BinaryTreeFind(root->left, x);
	if (leftRet)
		return leftRet;
	BTNode* rightRet = BinaryTreeFind(root->right, x);
	if (rightRet)
		return rightRet;
	//上面都没进就打印空
	return NULL;
}

二叉树层序遍历

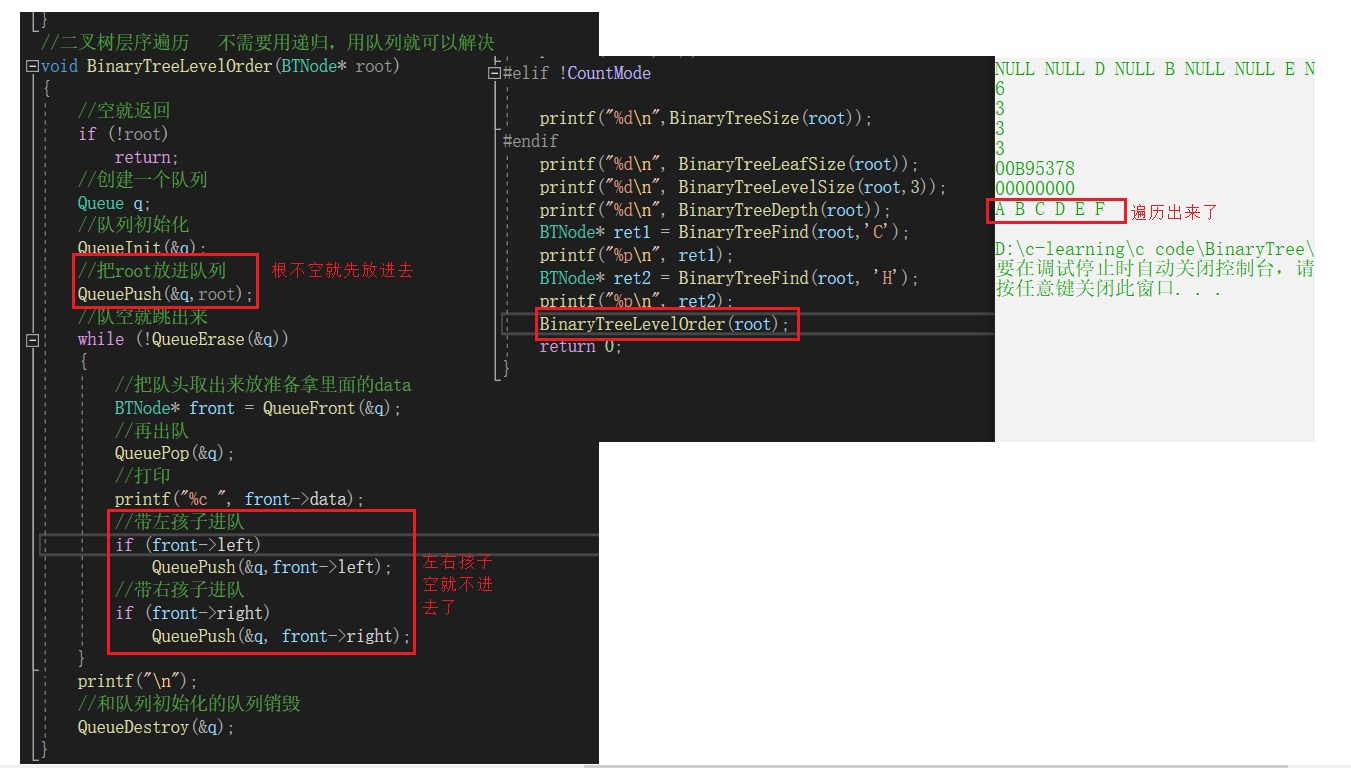
image-20211117085251571

//二叉树层序遍历   不需要用递归，用队列就可以解决
void BinaryTreeLevelOrder(BTNode* root)
{
	//空就返回
	if (!root)
		return;
	//创建一个队列
	Queue q;
	//队列初始化
	QueueInit(&q);
	//把root放进队列
	QueuePush(&q,root);
	//队空就跳出来
	while (!QueueErase(&q))
	{
		//把队头取出来放准备拿里面的data
		BTNode* front = QueueFront(&q);
		//再出队
		QueuePop(&q);
		//打印
		printf("%c ", front->data);
		//带左孩子进队
		if (front->left)
			QueuePush(&q,front->left);
		//带右孩子进队
		if (front->right)
			QueuePush(&q, front->right);
	}
	printf("\n");
	//和队列初始化的队列销毁
	QueueDestroy(&q);
}

判断二叉树是否是完全二叉树BinaryTreeComplete

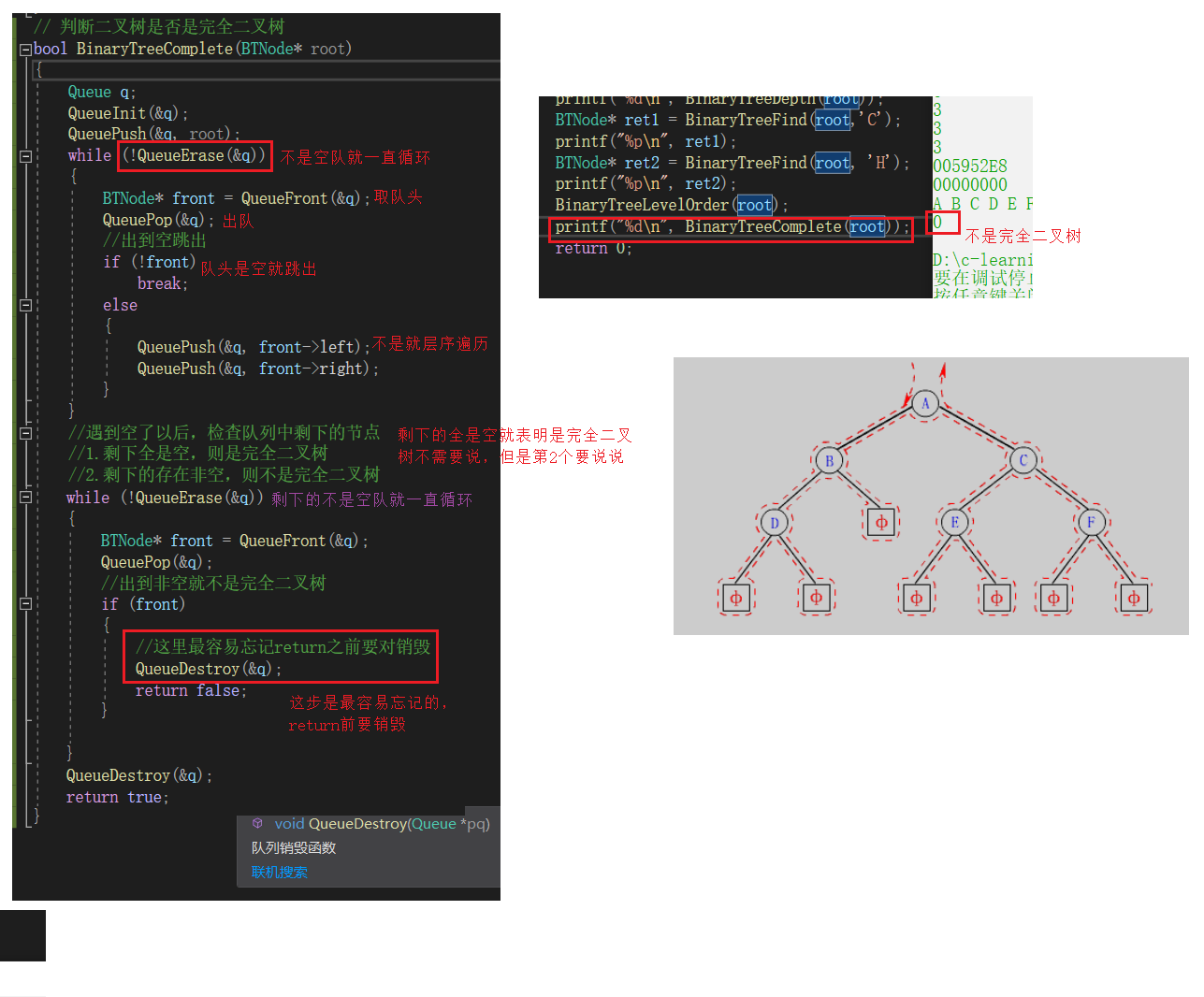
image-20211118000032718

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueErase(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//出到空跳出
		if (!front)
			break;
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}
	//遇到空了以后，检查队列中剩下的节点
	//1.剩下全是空，则是完全二叉树
	//2.剩下的存在非空，则不是完全二叉树
	while (!QueueErase(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//出到非空就不是完全二叉树
		if (front)
		{
			//这里最容易忘记return之前要对销毁
			QueueDestroy(&q);
			return false;
		}
		
	}
	QueueDestroy(&q);
	return true;
}

二叉树销毁BinaryTreeDestory

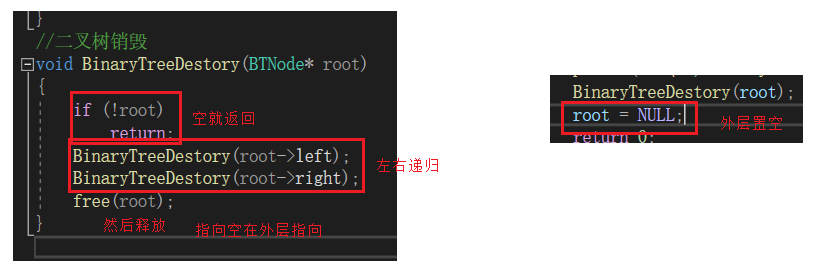
image-20211120002929144

//二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
	if (!root)
		return;
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}

代码

BinaryTree.h

#pragma once

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

#define CountMode 0


//二叉树数据类型
typedef char BTDataType;
//二叉树节点
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

//二叉树前序遍历
extern void PreOrder(BTNode* root);
//二叉树中序遍历
extern void InOrder(BTNode* root);
//二叉树后序遍历
extern void PostOrder(BTNode* root);
//获得节点函数
extern BTNode* BuyNode(BTDataType x);
#if CountMode
//二叉树节点个数
extern void BinaryTreeSize(BTNode* root, int* pn);
#elif !CountMode
//二叉树节点个数
extern int BinaryTreeSize(BTNode* root);
#endif
//二叉树叶子节点个数
extern int BinaryTreeLeafSize(BTNode* root);
//二叉树第k层节点个数
extern int BinaryTreeLevelSize(BTNode* root,int k);
//二叉树深度/高度
extern int BinaryTreeDepth(BTNode* root);
//二叉树查找值为x的节点
extern BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
//二叉树层序遍历   
extern void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
extern bool BinaryTreeComplete(BTNode* root);
//二叉树销毁
extern void BinaryTreeDestory(BTNode* root);

BinaryTree.c

#define _CRT_SECURE_NO_WARNINGS 1

#include"BinaryTree.h"
#include"Queue.h"

//获得节点函数
BTNode* BuyNode(BTDataType x)
{
	//创建二叉树节点
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	//检查是否成功创建
	assert(node);
	//把数据放到节点里
	node->data = x;
	//左右子树先空树
	node->left = node->right = NULL;
	return node;
}

//二叉树前序遍历
void PreOrder(BTNode* root)
{
	//不断言的原因是可以存在空树
	if (!root)//空树就直接返回
	{
		//想打印空也可以
		printf("NULL ");
		return;
	}

	printf("%c ",root->data);
	//递归左树
	PreOrder(root->left);
	//递归右树
	PreOrder(root->right);
}
//二叉树中序遍历
void InOrder(BTNode* root)
{
	//不断言的原因是可以存在空树
	if (!root)//空树就直接返回
	{
		//想打印空也可以
		printf("NULL ");
		return;
	}
	//不为空 递归左树
	InOrder(root->left);
	//打印数据
	printf("%c ",root->data);
	//递归右树
	InOrder(root->right);
}
//二叉树后序遍历
void PostOrder(BTNode* root)
{
	//不断言的原因是可以存在空树
	if (!root)//空树就直接返回
	{
		//想打印空也可以
		printf("NULL ");
		return;
	}
	//不为空 递归左树
	PostOrder(root->left);
	//递归右树
	PostOrder(root->right);
	//打印数据
	printf("%c ", root->data);
}
#if CountMode
//二叉树节点个数
void BinaryTreeSize(BTNode* root,int* pn)
{
	//不断言的原因是可以存在空树
	if (!root)//空树就直接返回
	{
		return;
	}
	(*pn)++;
	BinaryTreeSize(root->left, pn);
	BinaryTreeSize(root->right, pn);
}
#elif !CountMode
//二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right)+1;
}
#endif
//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (!root)//空树返回0
		return 0;
	if (!(root->left) && !(root->right))
		return 1;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
//二叉树第k层节点个数
int BinaryTreeLevelSize(BTNode* root, int k)
{
	//k小于等于零直接断言 因为都是从第一层开始的
	assert(k > 0);
	if (!root)
		return 0;
	if (1 == k)
		return 1;
	//root不等于空，k也不等于1，说明root这棵树的第k层节点在子树里面
	//转换成求左右子树的第k-1层节点数量
	return BinaryTreeLevelSize(root->left, k - 1) + BinaryTreeLevelSize(root->right, k - 1);
}
//二叉树深度/高度
int BinaryTreeDepth(BTNode* root)
{
	if (!root)
		return 0;
	//把递归的数用变量保存起来，减少资源的消耗
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (!root)
		return NULL;
	if (root->data == x)
		return root;
	BTNode* leftRet = BinaryTreeFind(root->left, x);
	if (leftRet)
		return leftRet;
	BTNode* rightRet = BinaryTreeFind(root->right, x);
	if (rightRet)
		return rightRet;
	//上面都没进就打印空
	return NULL;
}
//二叉树层序遍历   不需要用递归，用队列就可以解决
void BinaryTreeLevelOrder(BTNode* root)
{
	//空就返回
	if (!root)
		return;
	//创建一个队列
	Queue q;
	//队列初始化
	QueueInit(&q);
	//把root放进队列
	QueuePush(&q,root);
	//队空就跳出来
	while (!QueueErase(&q))
	{
		//把队头取出来放准备拿里面的data
		BTNode* front = QueueFront(&q);
		//再出队
		QueuePop(&q);
		//打印
		printf("%c ", front->data);
		//带左孩子进队
		if (front->left)
			QueuePush(&q,front->left);
		//带右孩子进队
		if (front->right)
			QueuePush(&q, front->right);
	}
	printf("\n");
	//和队列初始化的队列销毁
	QueueDestroy(&q);
}
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueErase(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//出到空跳出
		if (!front)
			break;
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}
	//遇到空了以后，检查队列中剩下的节点
	//1.剩下全是空，则是完全二叉树
	//2.剩下的存在非空，则不是完全二叉树
	while (!QueueErase(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//出到非空就不是完全二叉树
		if (front)
		{
			//这里最容易忘记return之前要对销毁
			QueueDestroy(&q);
			return false;
		}
		
	}
	QueueDestroy(&q);
	return true;
}
//二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
	if (!root)
		return;
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}

test.c

#define _CRT_SECURE_NO_WARNINGS 1

#include"BinaryTree.h"
#include"Queue.h"


//创建树 我们不学二叉树的增删查改原因就在这，我们想要啥树自己链一个就行，没必要增删查改
BTNode* CreatBinaryTree()
{
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');
	nodeA->left = nodeB;
	nodeA->right = nodeC;
	nodeB->left = nodeD;
	nodeC->left = nodeE;
	nodeC->right = nodeF;
	return nodeA;
}

int main()
{
	BTNode* root = CreatBinaryTree();
	//PreOrder(root);
	//InOrder(root);
	PostOrder(root);
	printf("\n");
#if CountMode
	int n1 = 0;
	BinaryTreeSize(root, &n1);
	printf("%d ",n1);
#elif !CountMode

	printf("%d\n",BinaryTreeSize(root));
#endif
	printf("%d\n", BinaryTreeLeafSize(root));
	printf("%d\n", BinaryTreeLevelSize(root,3));
	printf("%d\n", BinaryTreeDepth(root));
	BTNode* ret1 = BinaryTreeFind(root,'C');
	printf("%p\n", ret1);
	BTNode* ret2 = BinaryTreeFind(root, 'H');
	printf("%p\n", ret2);
	BinaryTreeLevelOrder(root);
	printf("%d\n", BinaryTreeComplete(root));
	BinaryTreeDestory(root);
	root = NULL;
	return 0;
}
【版权声明】本文为华为云社区用户原创内容，未经允许不得转载，如需转载请自行联系原作者进行授权。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
二叉树 数据结构
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入