最小二乘法的极大似然解释

xindoo 发表于 2022/04/15 23:23:52 2022/04/15

【摘要】　　最开始学习机器学习的时候，首先遇到的就是回归算法，回归算法里最最重要的就是最小二乘法，为什么损失函数要用平方和，而且还得是最小？仔细想想最小二乘法视乎很合理，但是合理在哪，怎么用数学方法来证明它合理。...

　　最开始学习机器学习的时候，首先遇到的就是回归算法，回归算法里最最重要的就是最小二乘法，为什么损失函数要用平方和，而且还得是最小？仔细想想最小二乘法视乎很合理，但是合理在哪，怎么用数学方法来证明它合理。

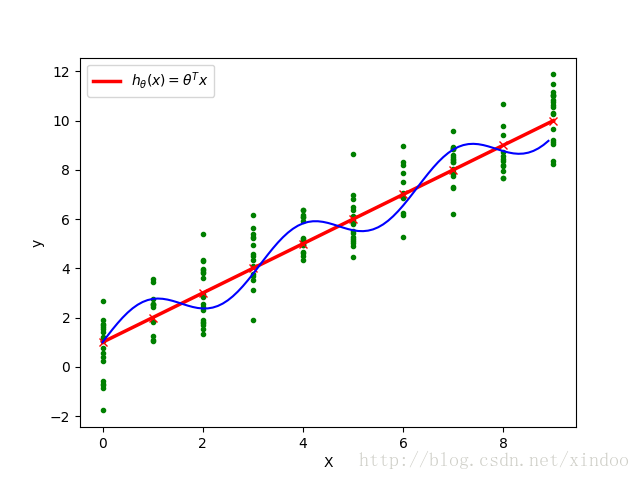
J (θ) = 1 2 \sum i = 1 m (h θ (x (i)) - y (i)) 2

hθ(x)

ε(i)(1≤i≤m)

σ2

y (i) = θ T x (i) + ϵ (i) p (ϵ (i)) = 1 2 π ‾ ‾ ‾ \sqrt σ e - ( ϵ ( i ) ) 2 2 σ 2 p (y (i) | x (i); θ) = 1 2 π ‾ ‾ ‾ \sqrt σ e (- ( y ( i ) - θ T x ( i ) ) 2 2 σ 2)

L (θ) = \prod i = 1 m p (y (i) | x (i); θ) = \prod i = 1 m 1 2 π ‾ ‾ ‾ \sqrt σ e (- ( y ( i ) - θ T x ( i ) ) 2 2 σ 2)

ℓ(θ)

ℓ (θ) = l o g L (θ) = l o g \prod i = 1 m 1 2 π ‾ ‾ ‾ \sqrt σ e (- ( y ( i ) - θ T x ( i ) ) 2 2 σ 2) = \sum i = 1 m 1 2 π ‾ ‾ ‾ \sqrt σ e (- ( y ( i ) - θ T x ( i ) ) 2 2 σ 2) = m l o g 1 2 π ‾ ‾ ‾ \sqrt σ - 1 σ 2 \cdot 1 2 \sum i = 1 m (h θ (x (i)) - y (i)) 2

12∑mi=1(hθ(x(i))−y(i))2

J (θ) = 1 2 \sum i = 1 m (h θ (x (i)) - y (i)) 2

Θ(n3)

J (θ) = 1 2 \sum i = 1 m (h θ (x (i)) - y (i)) 2 = 1 2 (X θ - y) T (X θ - y)

J(θ)

\nabla θ J (θ) = \nabla θ (1 2 (X θ - y) T (X θ - y)) = \nabla θ (1 2 (θ T X T - y T) (X θ - y)) = \nabla θ (1 2 (θ T X T X θ - θ T X T y - y T X θ + y T y)) = 1 2 (2 X T X θ - X T y - (y T X) T) = X T X θ - X T y

J(θ)

X T X θ - X T y = 0 X T X θ = X T y θ = (X T X) - 1 X T y

文章来源: xindoo.blog.csdn.net，作者：xindoo，版权归原作者所有，如需转载，请联系作者。

原文链接：xindoo.blog.csdn.net/article/details/78004521

0/1000

抱歉，系统识别当前为高风险访问，暂不支持该操作

上滑加载中

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。