Problem 5

2520 is the smallest number that can be divided by each of the numbers from 1 to 10 without any remainder.
What is the smallest positive number that is evenly divisible by all of the numbers from 1 to 20?

问题 5

2520 是可以除以 1 到 10 的每个数字而没有任何余数的最小数字。
能被 1 到 20 的所有数整除的最小正数是多少？

理论要点

最小公倍数

引用下百科的解释：

两个或多个整数公有的倍数叫做它们的公倍数，其中除 0 以外最小的一个公倍数就叫做这几个整数的最小公倍数
整数 $a,b$ 的最小公倍数记为 $[a,b]$ ，同样的， $a,b,c$ 的最小公倍数记为 $[a,b,c]$ ，多个整数的最小公倍数也有同样的记号

那如何计算最小公倍数呢?

首先，把这几个数的质因数写出来，最小公倍数等于它们所有的质因数的乘积（如果有几个质因数相同，则比较两数中哪个数有该质因数的个数较多，乘较多的次数）

例如：

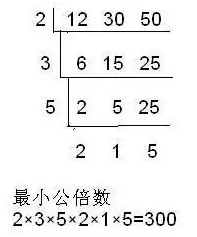
最大公约数

最大公约数， $a,b$ 的最大公约数记为 $(a,b)$

即：短除寻找公因数数，直到找不出公因数，左侧公因数乘积即为最大公约数

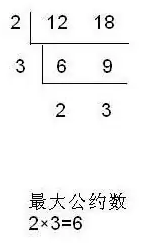
最大公约数和最小公倍数的关系

两个数的乘积等于这两个数的最大公约数与最小公倍数的乘积

若有两数 $a,b$，它们的最大公约数是 $p$，最小公倍数是 $q$

那么

$$\large a×b=p×q$$

该公式可改写为

$$\large a×b=gcd\left (a,b \right)×q$$

那么，我们给出最小公倍数的计算公式

$$\large lcm(a,b)=\frac{ab}{gcd(a,b)}=q$$

欧几里得算法

又称辗转相除法，用于计算两个非负整数 $a,b$ 的最大公约数

• 用较小数除较大数
• 再余数（第一余数）去除除数
• 再用出现的余数（第二余数）去除第一余数
• 迭代，直到最后余数是0为止。若要求两个数的最大公约数，则最后的除数就是这两个数的最大公约数

计算公式

$$\large gcd\left (a,b \right)$$

思路分析

根据欧几里得算法计算公式，计算得到两数最大公约数，再由最小公倍数计算公式得出最小公倍数。然后让两个数的最小公倍数和第三个数计算最小公倍数，迭代求算即可

代码实现

/*
 * @Author: coder-jason
 * @Date: 2022-04-11 14:08:31
 * @LastEditTime: 2022-04-11 14:59:47
 */
#include <iostream>
using namespace std;

typedef long long variable; // 定义类型别名

variable gcd(variable a, variable b) // gcd 实现
{
    return b>0 ? gcd(b, a % b) : a;
}

int main()
{
    variable ans = 1;
    for (int i = 2; i <= 20; i++)
    {
        ans = ans * i / gcd(ans, i);
    }
    cout << ans << endl;
    return 0;
}

答案：232792560