计算机组成原理-第二章 数据表示与运算
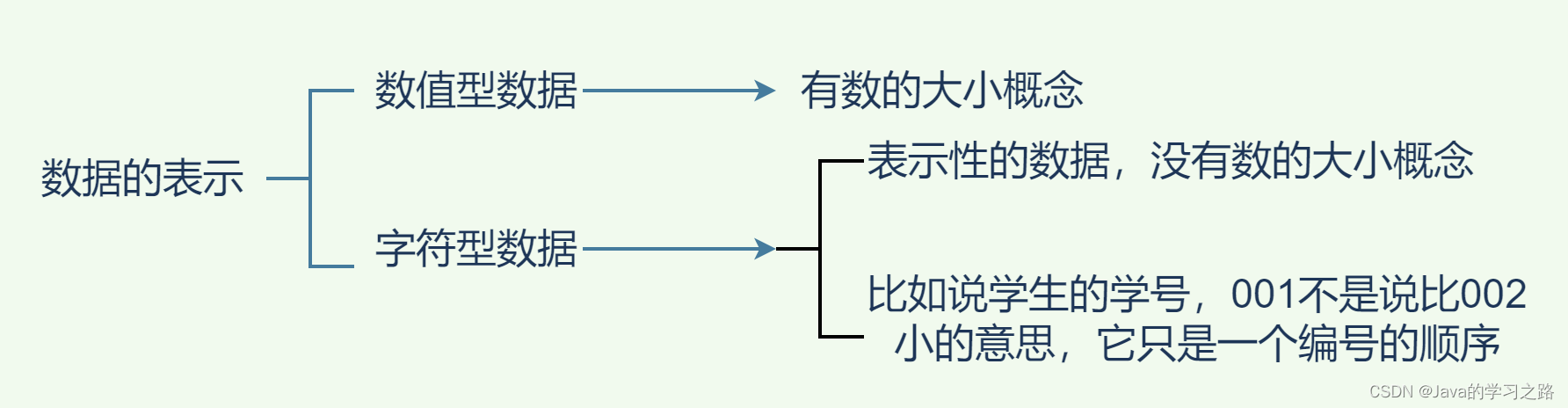
一、数据的表示
这一部分会讲解数值型数据和字符型数据
1.数值型数据的表示(重点难点)
计算机采用二进制来表示数据,但是用二进制来表示数据的话,它的位数就会很多,所以就需要八进制,十六进制等其他进制位来表示,可以简化表示。
1.1数值型数据的表示–进位制
数值型表示的三个方面

进位制
进位制也就是进位计数制
对于任何一种进制—X进制,就表示每一位上的数运算时都是逢X进一位。 十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,X进制就是逢X进位。
我们可以用若干位的组合表示一个数,形成一串符号序列,如:

比如说十进制的65,我们其实是这样算出来的:
十进制代表它的基数是10
它表示的大小为6×10^1 +5×10^0 =65
计算机中采用进位制
| 进位制 | 符号 | 基数 | 可以用来表示的数符 |
|---|---|---|---|
| 二进制 | B | 2 | 0,1 |
| 八进制 | O | 8 | 0到7 |
| 十进制 | D | 10 | 0到9 |
| 十六进制 | H | 16 | 0到9,A到F,A表示10,F表示15 |


BCD码简单来说就是把各个位置的数字拆开,不看成一个整体,比如说10,用BCD码来表示的话,它就会分别表示1和0,就像我们在电脑上用键盘输入10的时候,是先敲出1,再敲出0,然后再把他们结合起来成为10
各种进位制之间的转换
转换的首要原则
——整数部分与小数部分分开转换

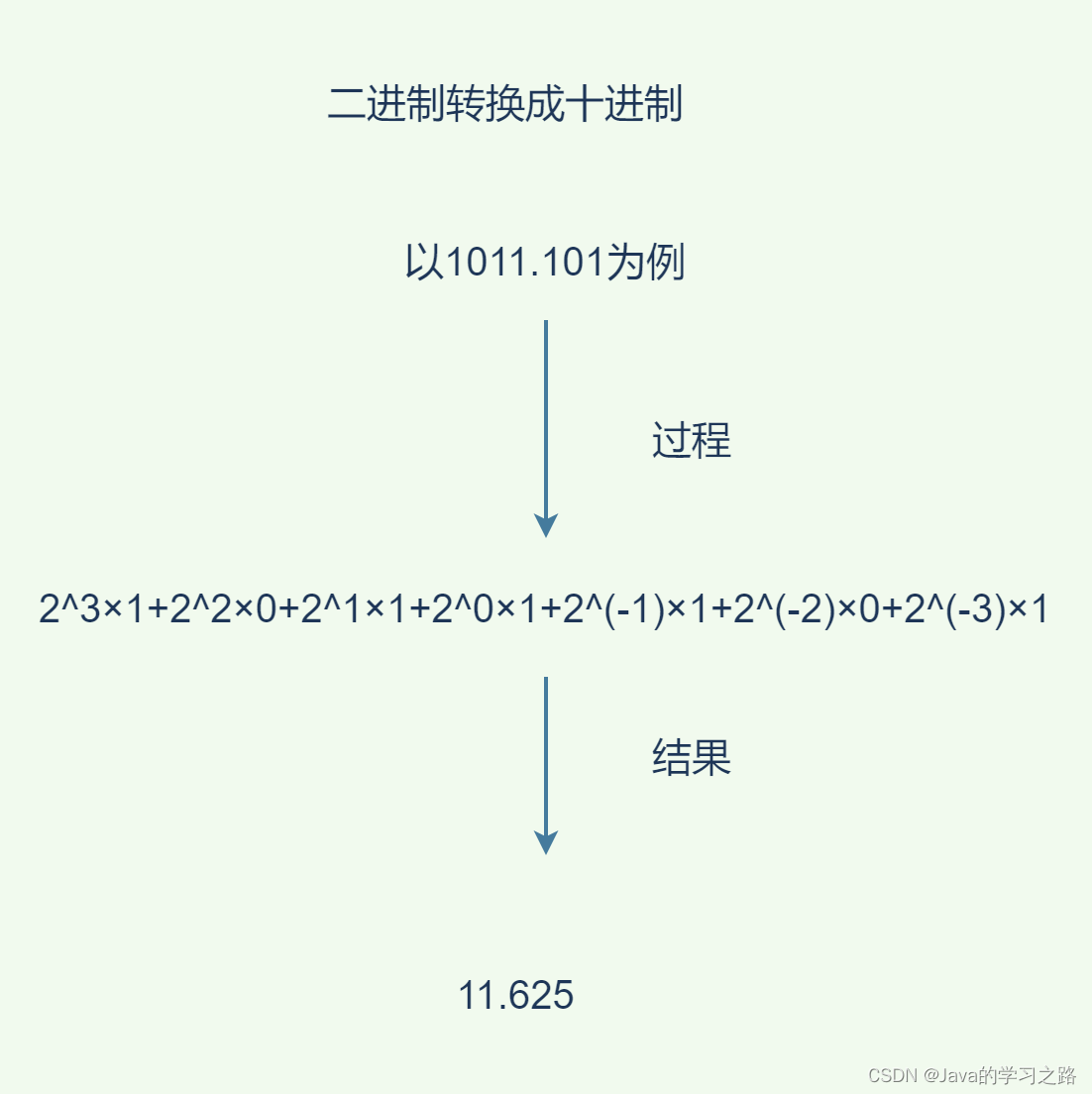
例题解析
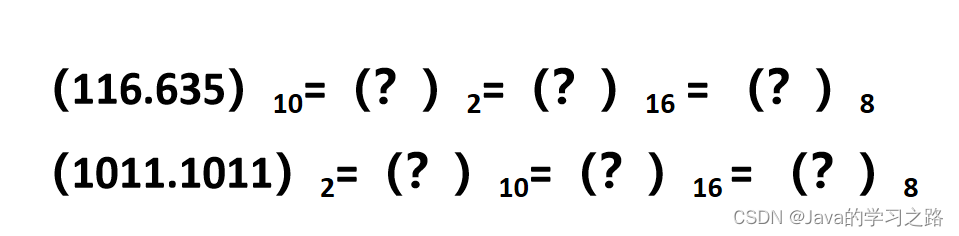


其他也是类似的,这里就不再多说,大家可以自己试试。
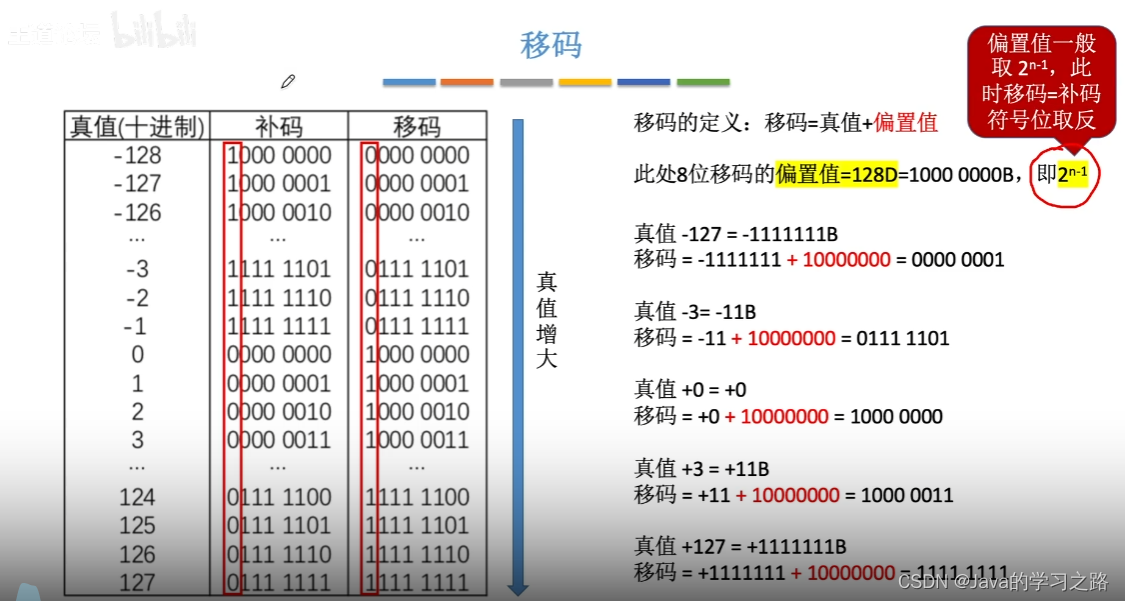
1.2数值型数据表示-码制
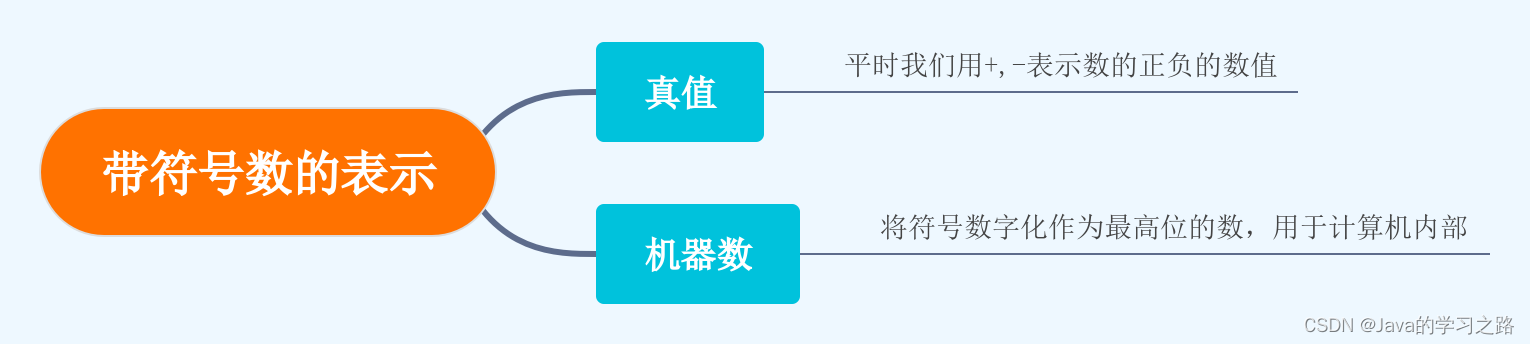
符号的数字化:用0表示+,用1表示-,因为计算机是用二进制来存储数据的
计算机里面是没有小数点的,我们看到的那些用小数点表示的数,只是我们为了方便看而自己写的小数点
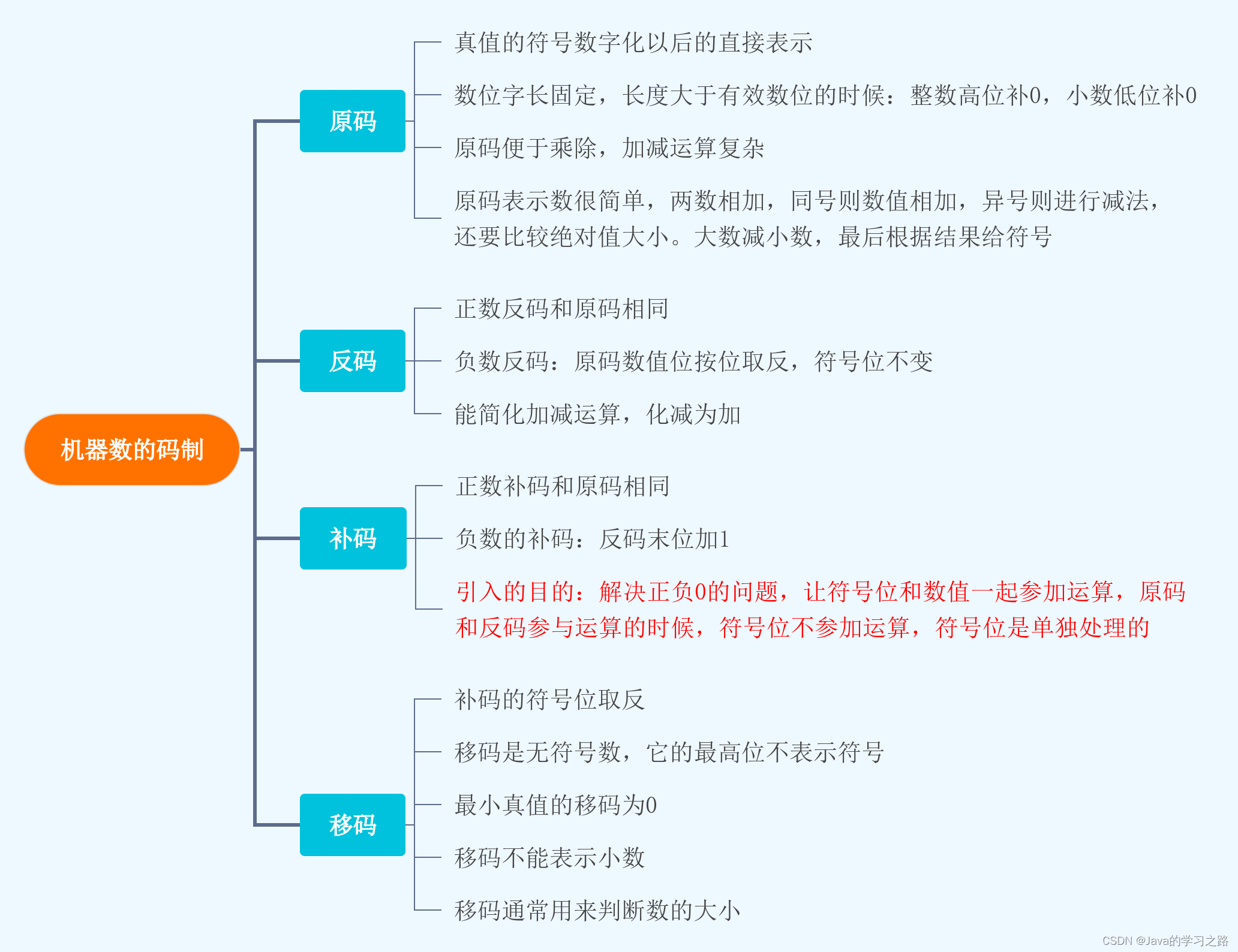
移码通常用来表示浮点数的阶码,阶码是k位整数,

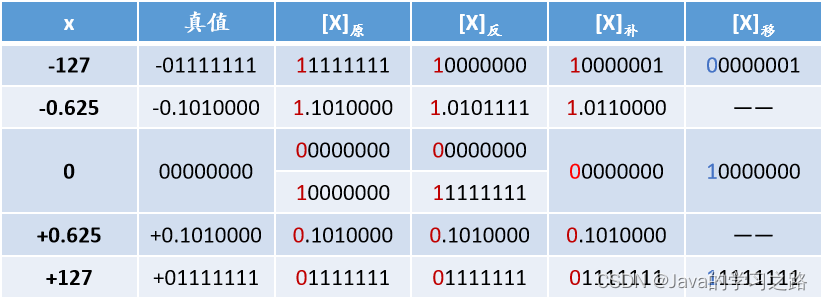
题目:假定编译器规定 int 和 short 类型长度占 32 位和 16 位,执行下列 C 语言语句后得到 y 的机器数为( B )
unsigned short x = 65530; unsigned int y = x;
A. 0000 7FFA B. 0000 FFFA C. FFFF 7FFA D. FFFF FFFA
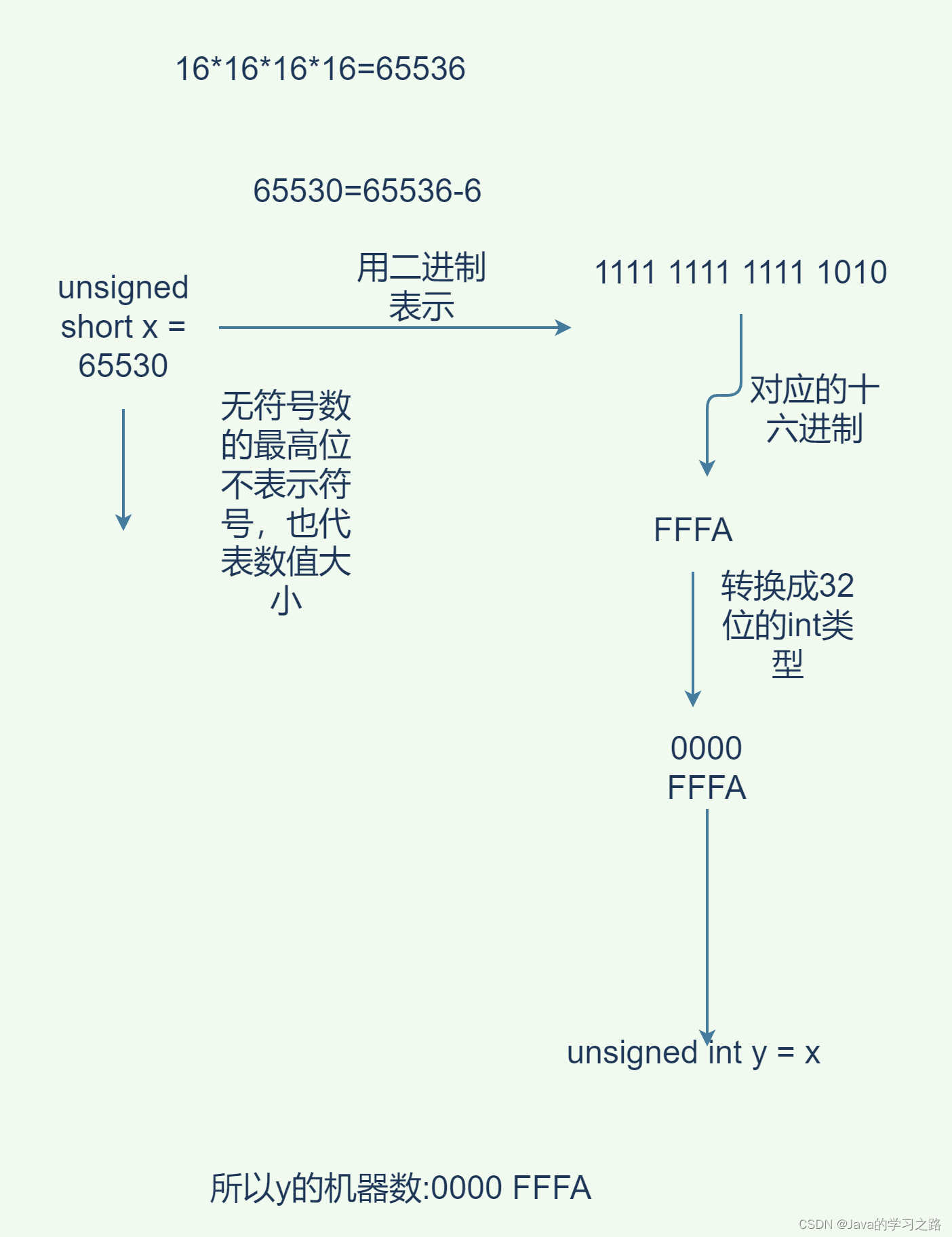
题目:由3个“1”和5个“0”组成的8位补码,能表示的最小整数是( B)
A. -126 B. -125 C. -32 D. -3
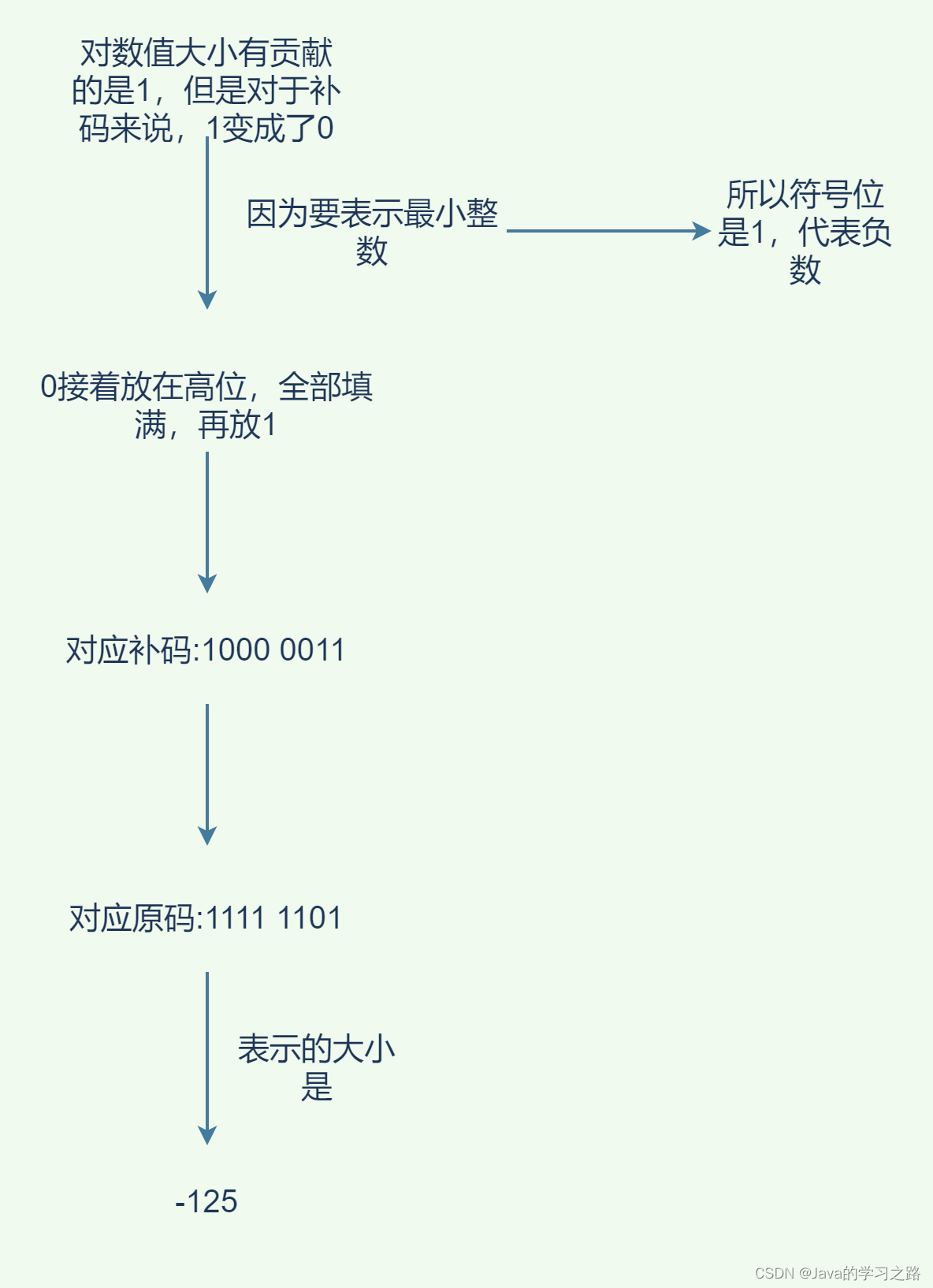
在选择计算机的数的表示方式的时候,要考虑下面的几个因素
①要表示的数的类型(小数,整数,实数和复数)
②可能的数的范围
③数值精确度
④数据存储和处理所需要的硬件代价
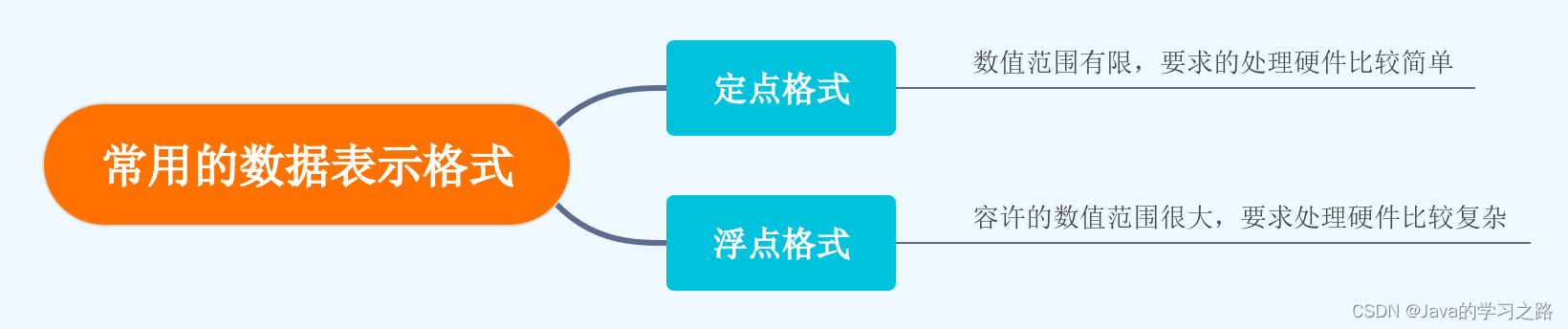
1.3数值型数据的表示——定点数
定点格式约束机器中所有数据的小数点位置固定不变,这个位置在计算机电路设计的时候定好了,因为已经约定好了在固定的位置,小数点就不再用记号.来表示
小数点位置固定在哪里都可以,但是通常把数据表示成纯整数或纯小数




1.4数值型数据的表示——浮点数
浮点数是指小数点的位置可以根据需要移动的数
表示格式

一台机器的阶码要么是移码要么是补码,不可能两个都用。
注意:浮点数的数值部分的绝对值<1

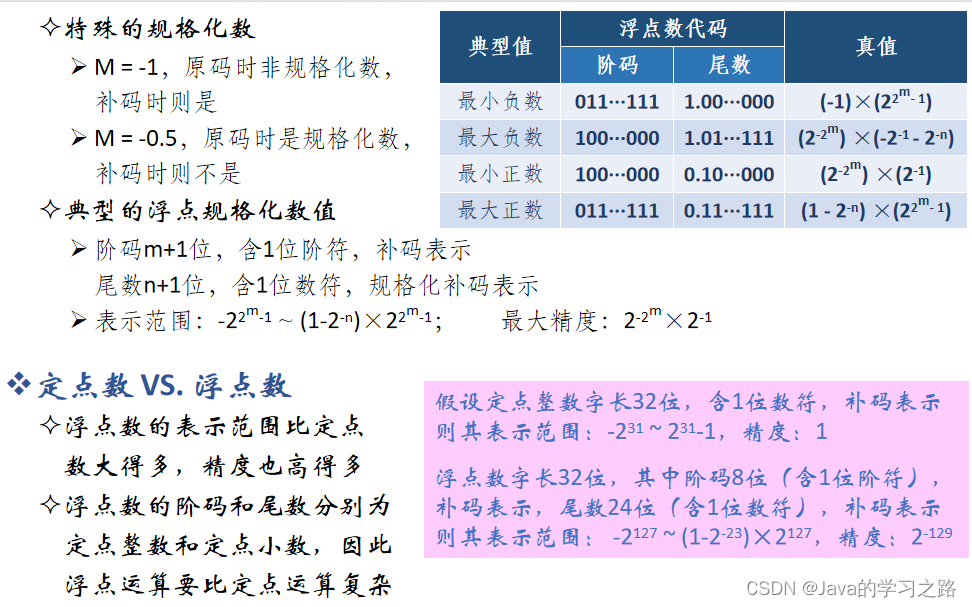

注:说明一下上面那个表示的最小的数:不管多少位的补码,它能表示的数最小是-1,一位是符号位,补码是反码+1,反码绝对值最大是11111111…1,再加1就变成10000000000000…0,但是需要注意的是,浮点数的数值部分是小数,所以补码绝对值最大是1
我们一般是用定点整数表示阶码,定点小数表示尾数
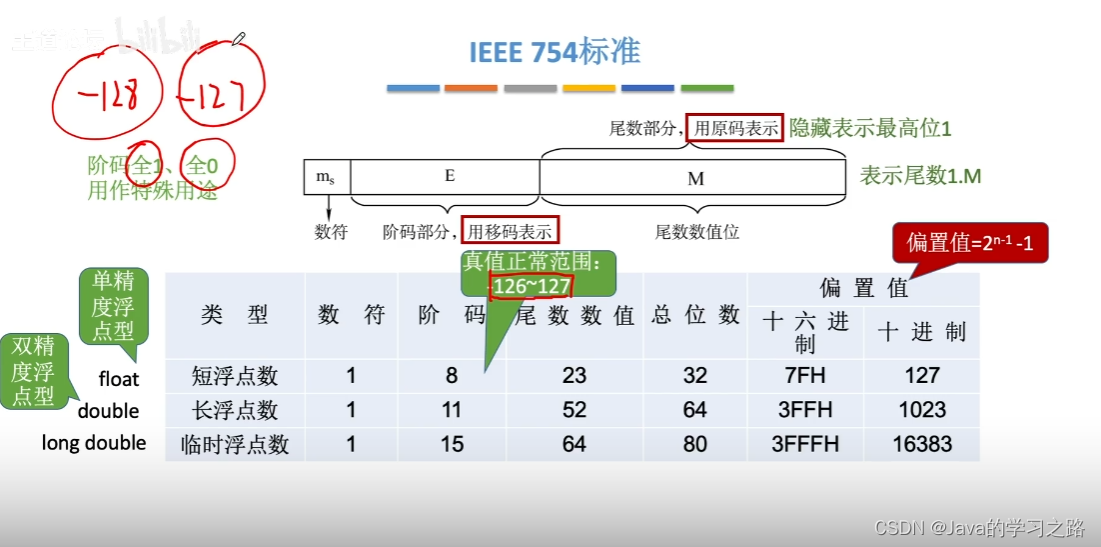
1.5浮点数表示的IEEE 754标准
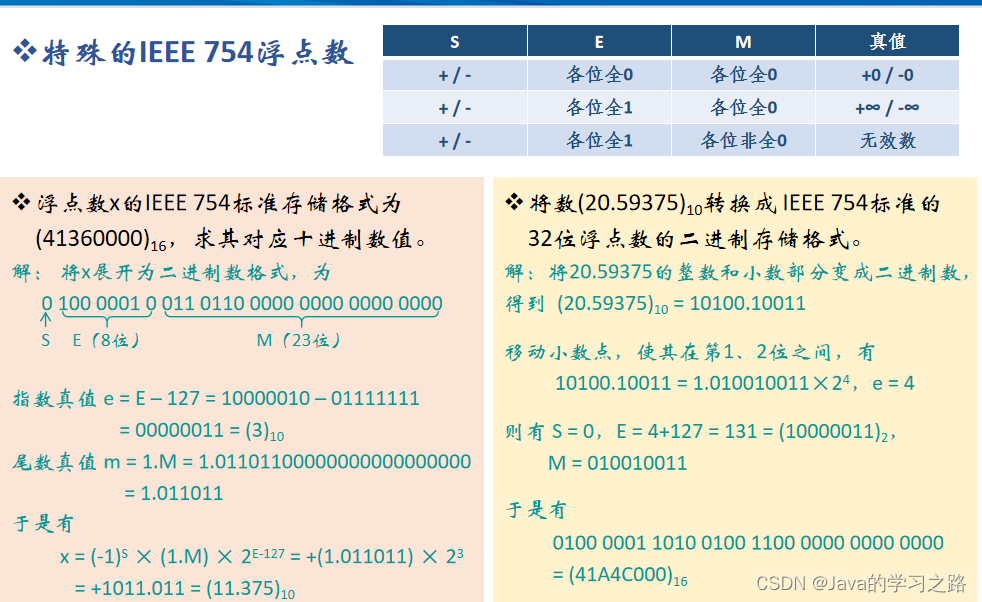
早期,各个计算机系统的浮点数使用不同的机器码来表示阶和尾数,这样就导致数据的交换和比较很麻烦,因为它们的表示不一样,所以当前计算机都用统一的IEEE 754标准中的格式来表示浮点数。
基数2是固定常数,所以不需要显示表示它
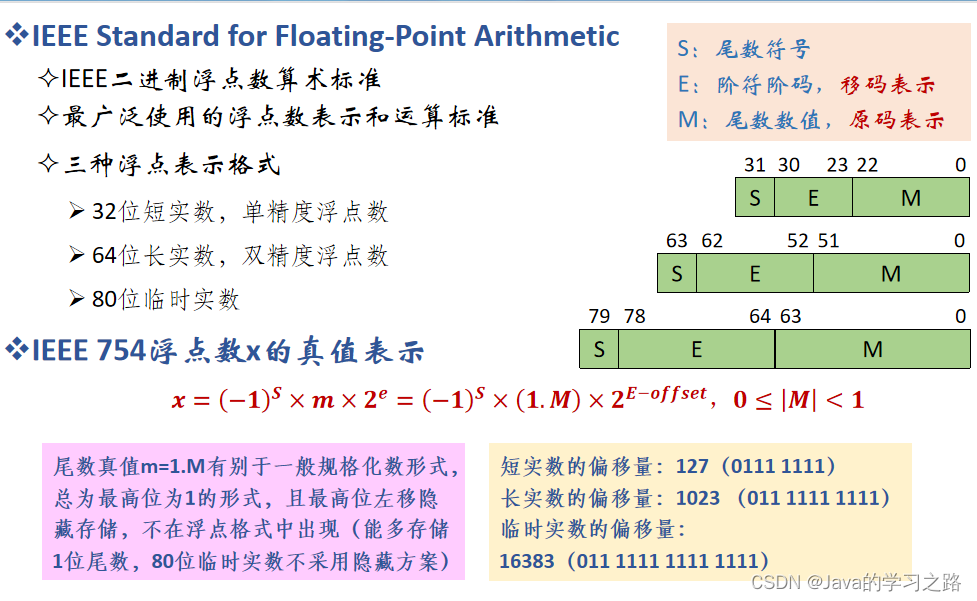
ps:移码是无符号数,所以阶码阶符一起
在IEEE 754标准中,阶码是用移码来表示的
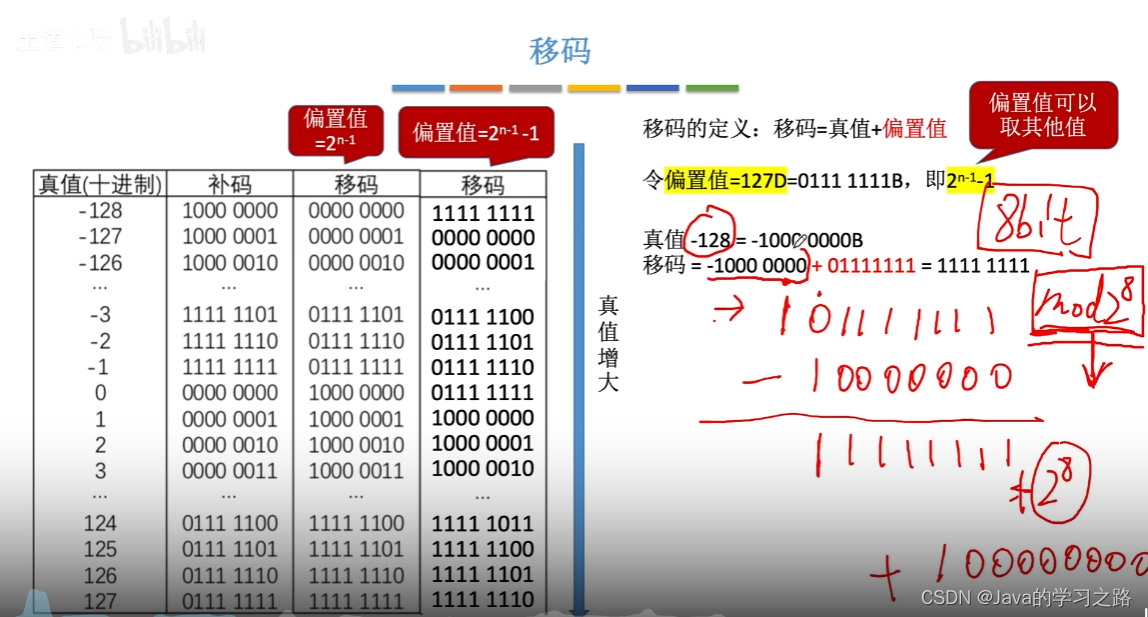
移码的定义:移码=真值+偏置值,偏置值是2的k次方。
在IEEE 754标准中,偏置值为+127
之前说过对于浮点数来说,它的尾数如果是用原码表示,我们希望它的最高有效位是1,我们就可以隐藏表示最高位1
移码=真值+偏置值
阶码真值=移码-偏置值
2.字符型数据表示

二、数据的运算方法
1.基本概念
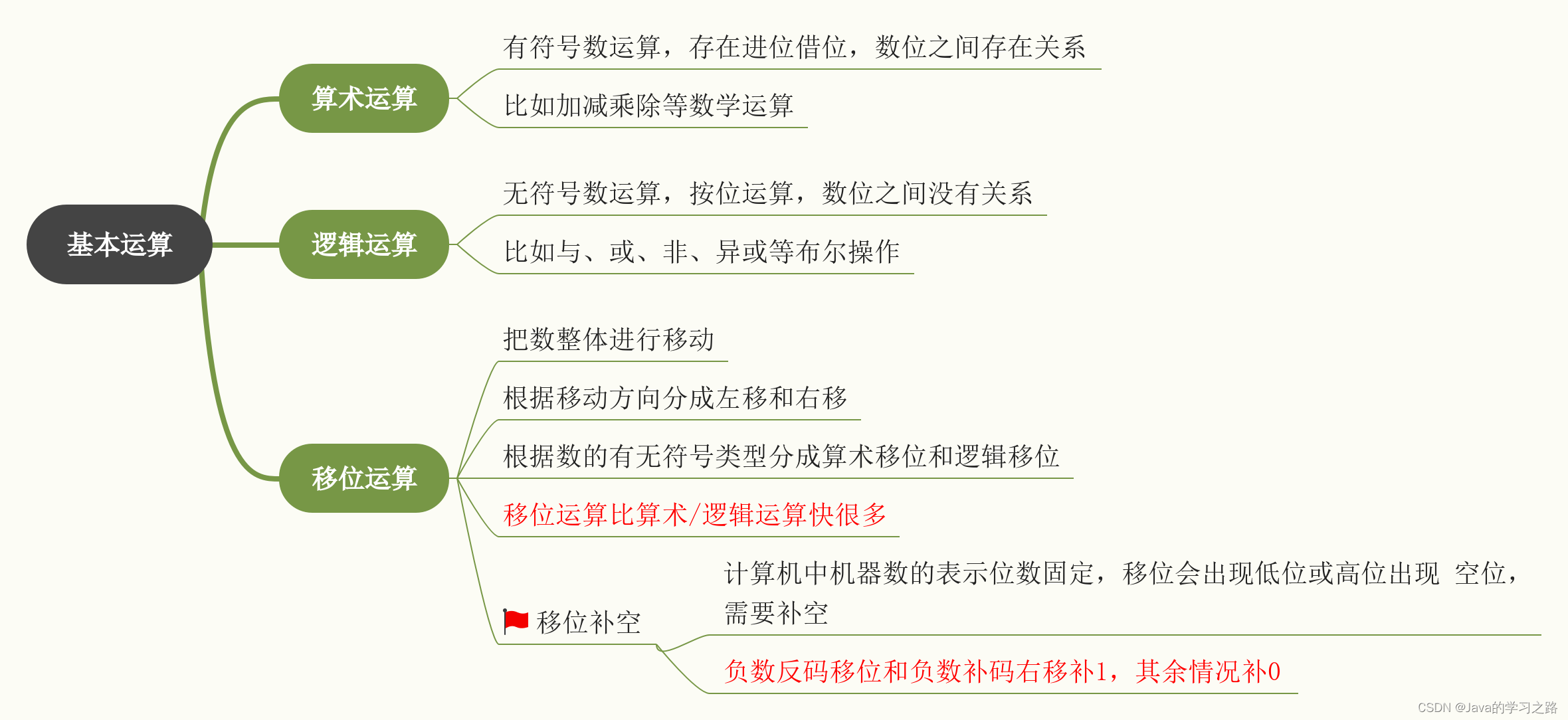
2.定点四则运算
计算机中定点加减运算都采用补码进行

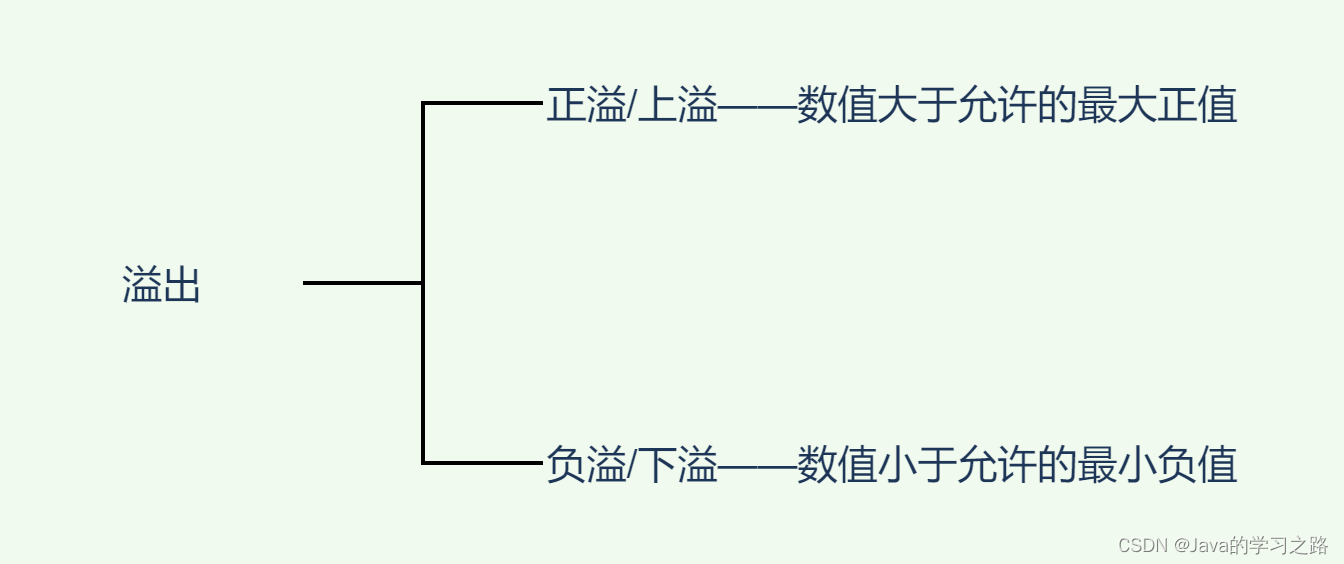
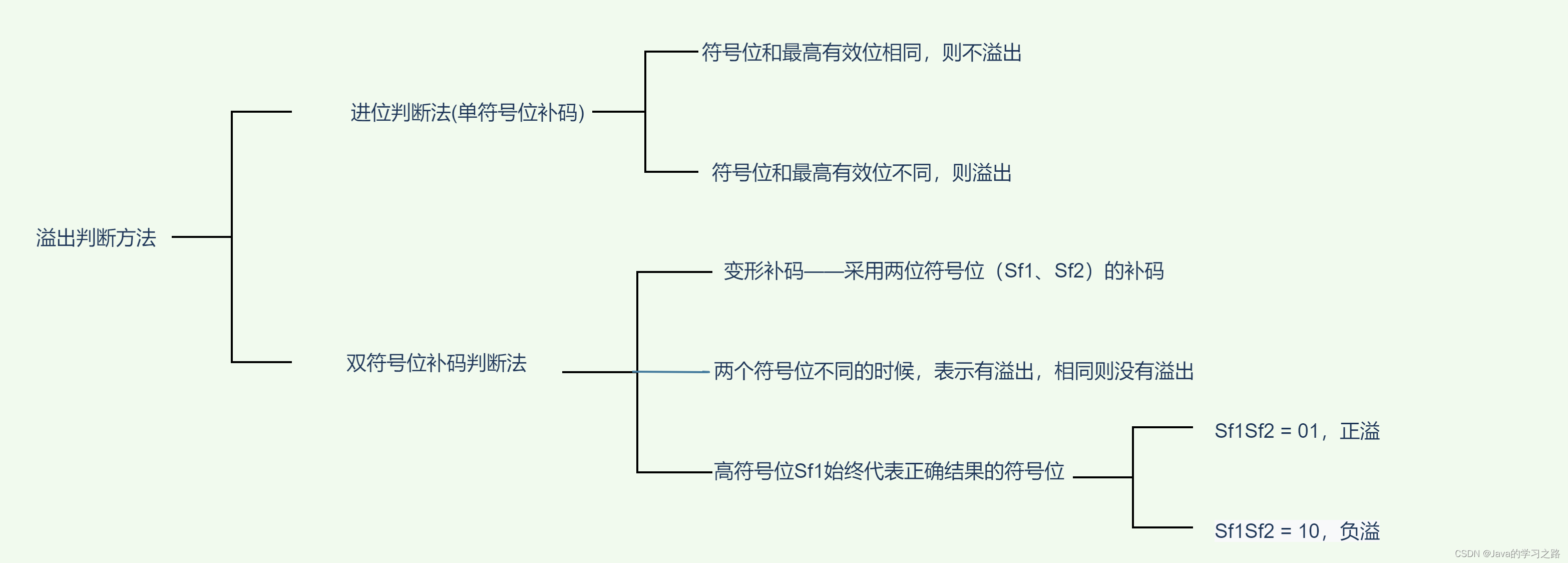
3.溢出判断
数据的值超过了机器数表示的范围
对于加法:只有两个符号相同的数相加,才会溢出
对于减法:只有符号相反相减,才会溢出

4. 舍入处理

注意:原码是0舍1入,补码是1舍0入
5.定点乘法运算
在做乘法运算的时候,我们从小学开始,就是一位一位的相乘,然后把每一步的乘积相加就是最后的结果,但是用计算机来实现的时候,是会出现问题的

1.原码一位乘法
符号单独处理,两个操作数绝对值相乘,每次把一位乘数对应的部分积和原来部分积的累加和进行相加,并右移。

2.补码一位乘法
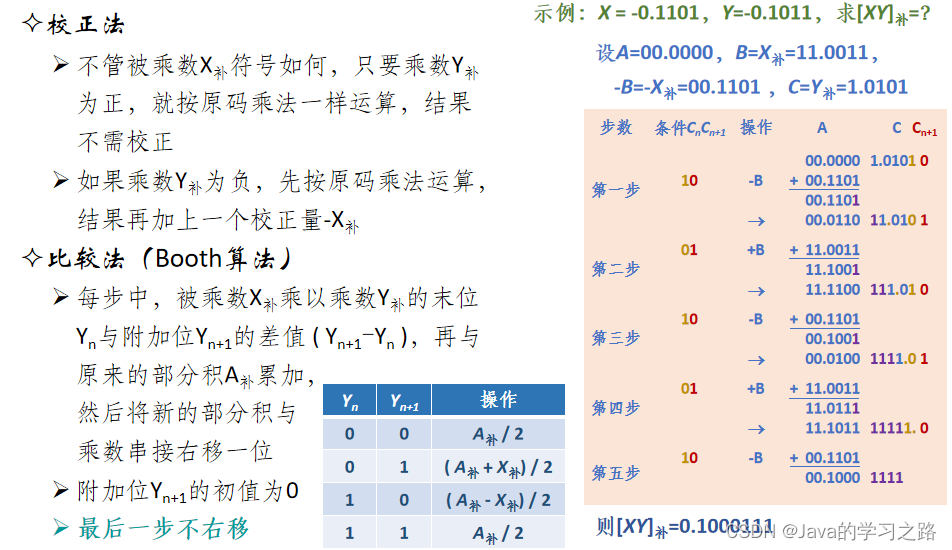
3.原码两位乘法
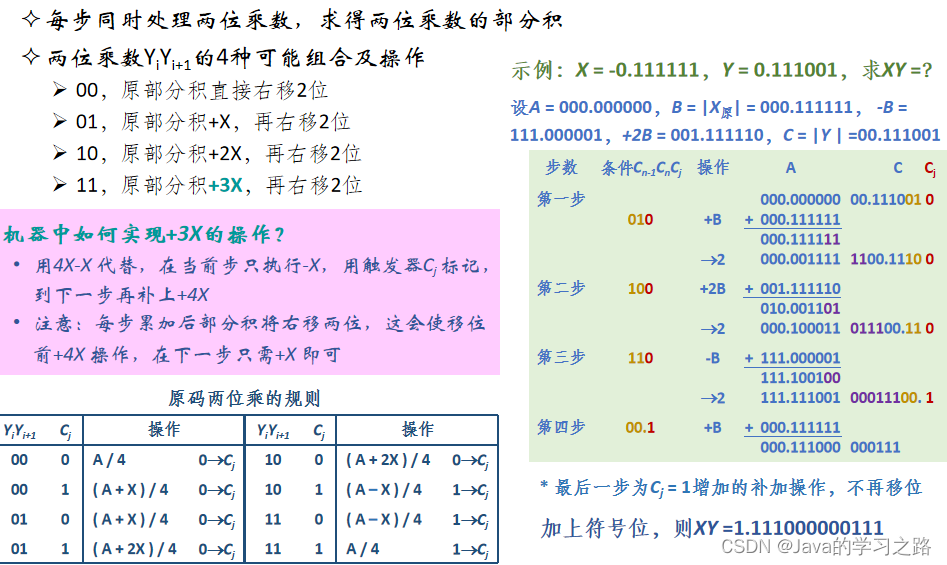
4.定点除法运算

6.浮点四则运算

三、数据的校验
1.奇偶校验码
校验是为了检测我们读取的信息是否正确,当信息符号某种规律的时候,我们就可以验证信息是正确的。
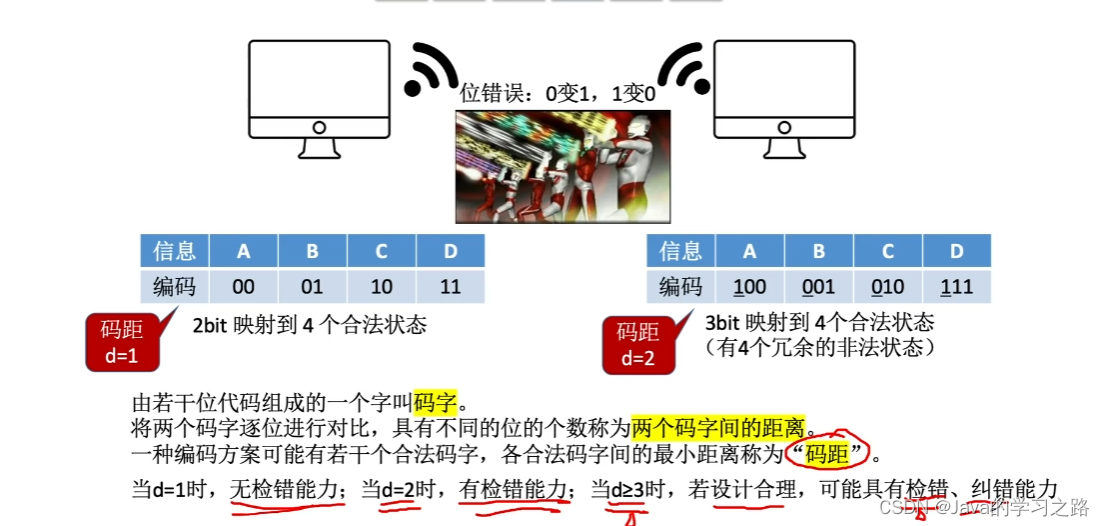
码距是用来判断一个码制的冗余度,评估其差错和纠错能力。
冗余校验
在信息写入时,增加部分代码(校验位/冗余位),将有效信息与校验位一起按约定的校验规律进行编码(校验码)存储;读出时,对读到的校验码进行校验(译码),看是否仍符合约定的校验规律
校验规律选择得当,不仅能够查错,而且可以纠错
比如说,根据上面的图片,第一种方案,码距为1,当信息某些位发生错误,由于码距为1,所以获得的信息也是正确的,我们就无法判断之前的信息是什么。方案2,码距为2,如果信息只有一位发生改变,那么得到的信息就不符号我们的校验规则,我们就能判断这个信息是错误的,所以码距可以用来评估纠错能力。
奇校验——使完整的校验码(有效位+校验位)中“1”的个数为奇数个
偶校验——使完整的校验码(有效位+校验位)中“1”的个数为偶数个
奇偶校验的缺陷:如果数据中有偶数个代码位错误,那么我们是无法检测出错误的,奇偶校验只能检测出奇数位错误,没有纠错能力。校验位只能携带2种状态信息,只能反馈是对或错两种状态,而不能反馈是哪一位错误
校验位的形成在数电中有学过,就是通过异或运算, 把所有有效位进行异或运算,得到的数据就是校验位。(不清楚的可以去看看数电)
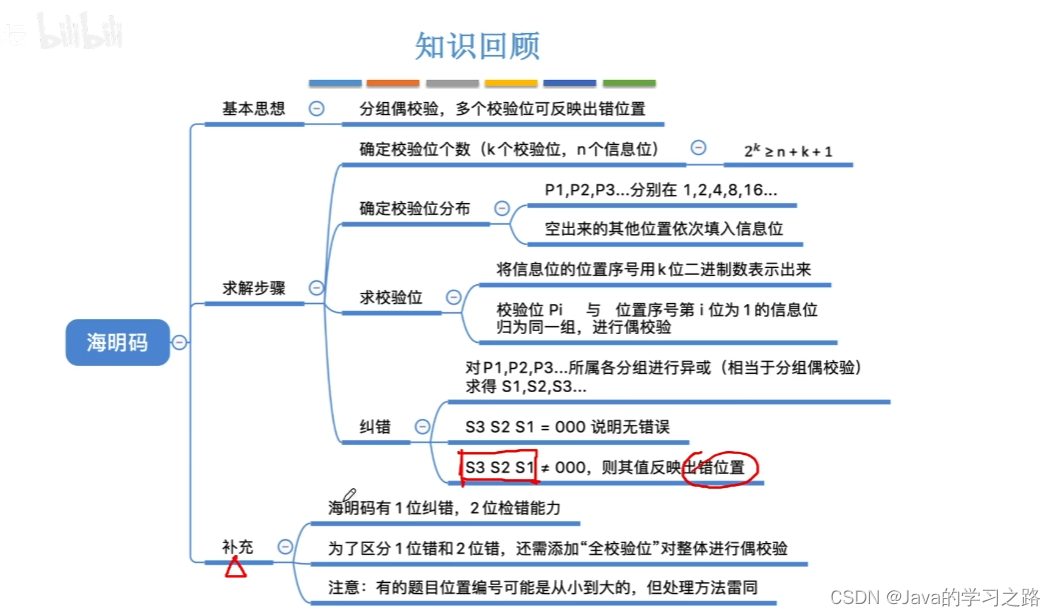
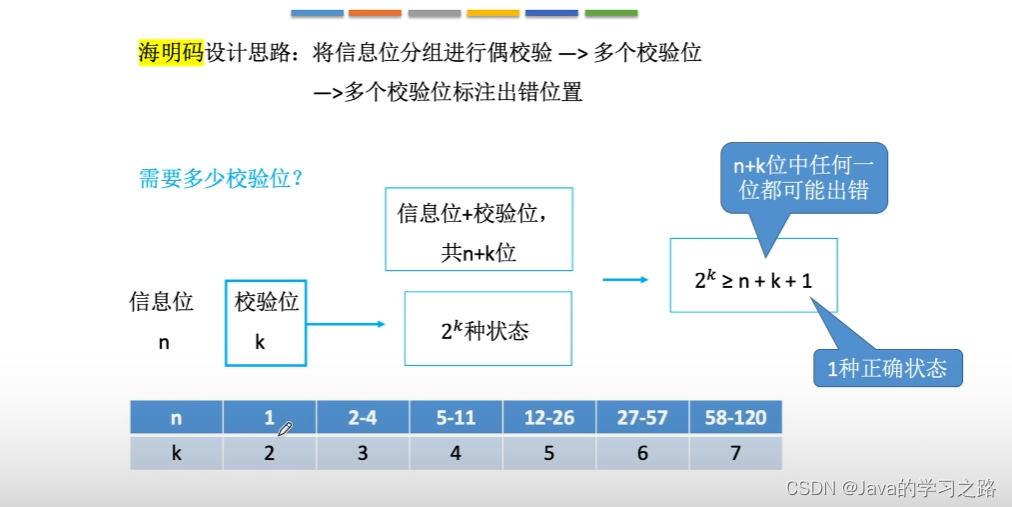
2.海明校验码
海明校验方法
采用多重奇偶校验的思想
将有效位按照一定规律组织成若干组,分组进行奇偶校验,每一个分组对应一个校验位
各组校验位组成一个指示错误的字,用于检测是否出错并能纠正一位错误。
这种方法除了能够反馈对错这样的状态信息,甚至还能指明是哪一个位置发生错误。
如果异或之后,得到的数据是010,说明出错的位置是2,也就是H2,如果得到的数据是110,说明出错的位置是6,也就是H6这个位置
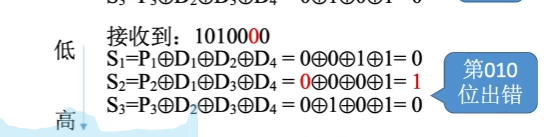
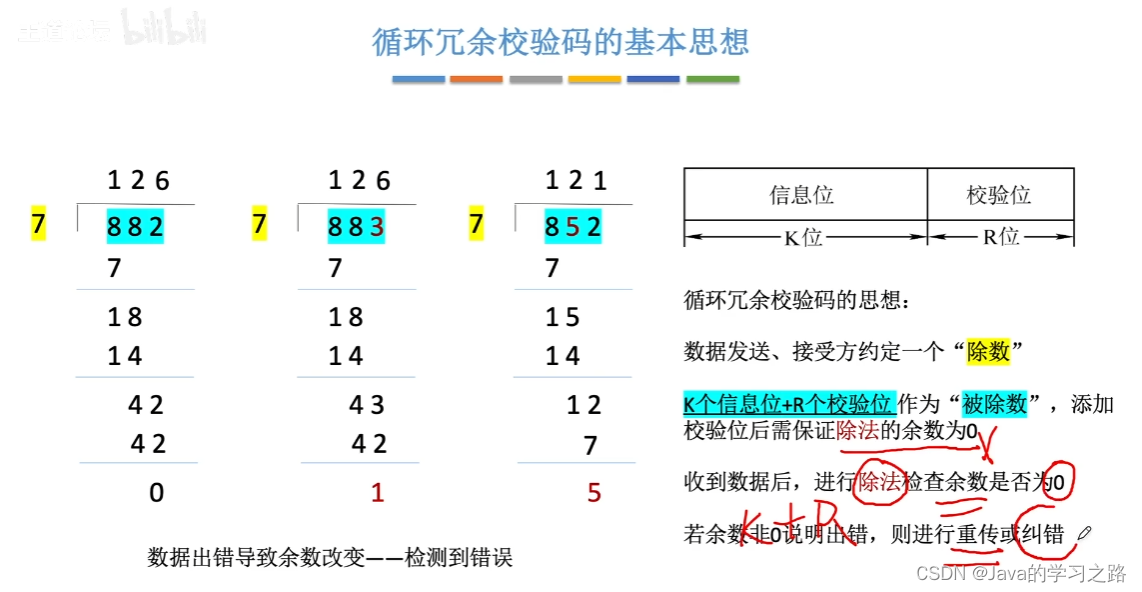
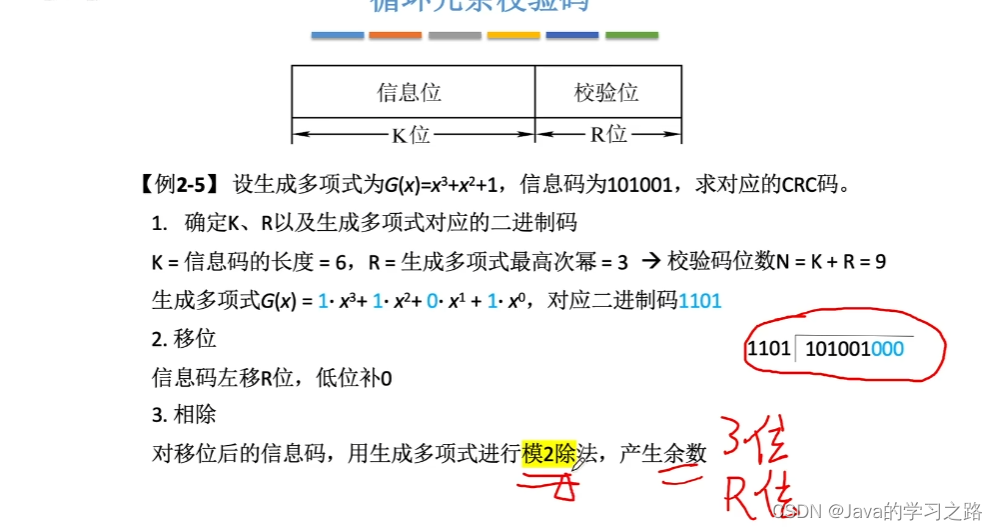
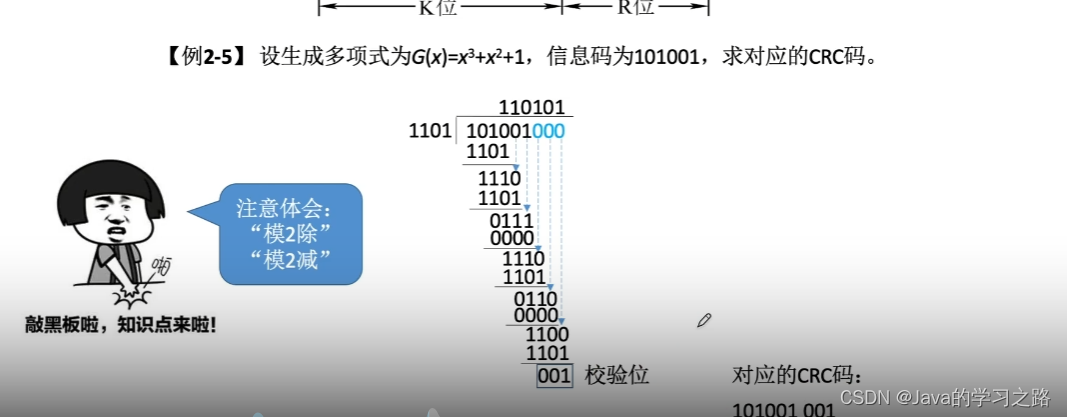
3.循环冗余校验码(CRC)
思想:
让校验码能被某一约定的代码除尽。若能除尽,则校验码正确,否则,余数指明出错位置
注:模2减也就是异或运算
最后就是检错了
- 点赞
- 收藏
- 关注作者

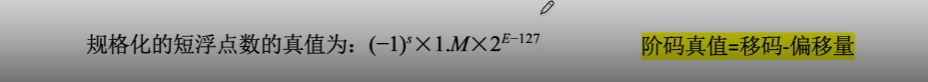




评论(0)