92. 将有序数组转换为二叉搜索树

难度：简单

收藏

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

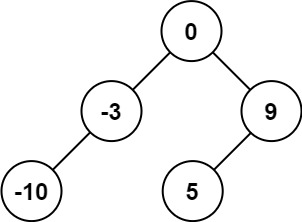
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

  

 

  
1
  
2
  
3
 

示例 2：

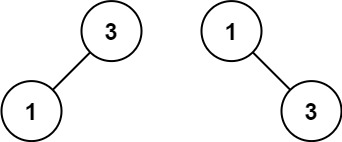
输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

  

 

  
1
  
2
  
3
 

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 按 严格递增 顺序排列

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
def build(nums:List[int],l:int,r:int)->TreeNode:
    if l>r:
        return None
    mid = l+r >>1
    root = TreeNode(nums[mid])
    root.left = build(nums,l,mid-1)
    root.right = build(nums,mid+1,r)
    return root
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        return build(nums,0,len(nums)-1)

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
 

\90. 从中序与后序遍历序列构造二叉树

难度：中等

收藏

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

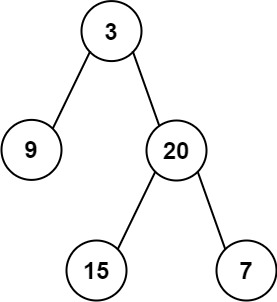
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

  

 

  
1
  
2
 

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

  

 

  
1
  
2
 

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
pos = {}
def dfs(post:List[int],In:List[int],pl:int,pr:int,il:int,ir:int)->TreeNode:
    if pl>pr:
        return None
    k = pos[post[pr]]-il
    root = TreeNode(post[pr])
    root.left=dfs(post,In,pl,pl+k-1,il,il+k-1)
    root.right=dfs(post,In,pl+k,pr-1,il+k+1,ir)
    return root
class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        n = len(inorder)
        for i in range(n):
            pos[inorder[i]]=i
        return dfs(postorder,inorder,0,n-1,0,n-1)

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
 

\136. 多数元素

难度：简单

收藏

给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：[3,2,3]
输出：3

  

 

  
1
  
2
 

示例 2：

输入：[2,2,1,1,1,2,2]
输出：2

  

 

  
1
  
2
 

进阶：

• 尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        r,c=0,0
        for x in nums:
            if not c:
                r=x
                c=1
            elif r==x:
                c+=1
            else:
                c-=1
        return r

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
 

\46. 最大子数组和

难度：简单

收藏

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

  

 

  
1
  
2
  
3
 

示例 2：

输入：nums = [1]
输出：1

  

 

  
1
  
2
 

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

  

 

  
1
  
2
 

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104

**进阶：**如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        res=-1<<80
        last=0
        for i in range(len(nums)):
            last=nums[i]+max(last,0)
            res=max(res,last)
        return res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

\89. 从前序与中序遍历序列构造二叉树

难度：中等

收藏

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

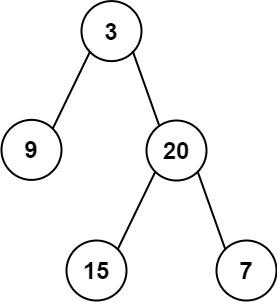
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

  

 

  
1
  
2
 

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

  

 

  
1
  
2
 

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
pos = {}
def dfs(pre:List[int],In:List[int],pl:int,pr:int,il:int,ir:int):
    if pl>pr:
        return None
    k= pos[pre[pl]]-il
    root=TreeNode(pre[pl])
    root.left=dfs(pre,In,pl+1,pl+k,il,il+k-1)
    root.right=dfs(pre,In,pl+k+1,pr,il+k+1,ir)
    return root
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        n = len(preorder)
        for i in range(n):
            pos[inorder[i]]=i
        return dfs(preorder,inorder,0,n-1,0,n-1)

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
 

文章来源: blog.csdn.net，作者：irrationality，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/weixin_54227557/article/details/123327753