Author:AXYZdong 自动化专业 工科男
有一点思考,有一点想法,有一点理性!
定个小小目标,努力成为习惯!在最美的年华遇见更好的自己!
1. 状态空间描述的建立
1.1 由系统框图建立空间状态描述

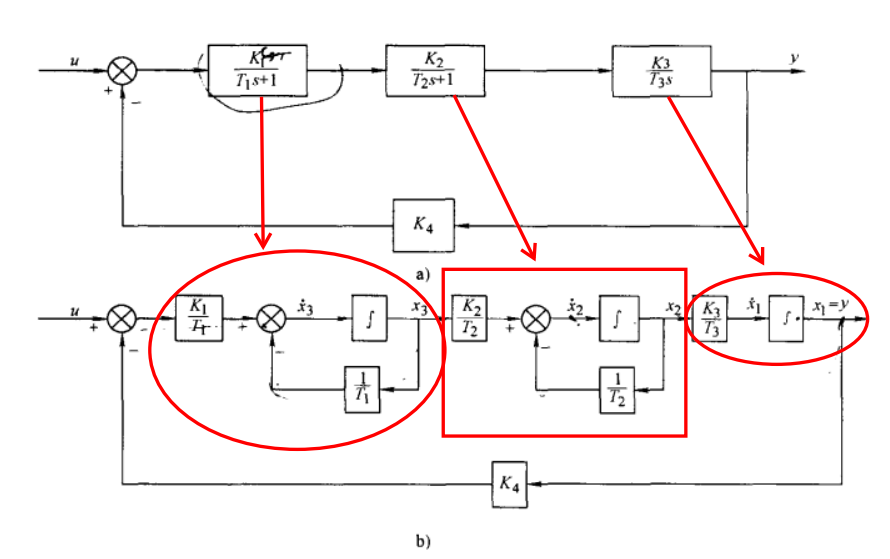
▲ a) 系统框图;b)系统模拟结构图
由图可知:
状态方程:⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧x1ˊ=T3K3x2x2ˊ=−T21x2+T2K2x3x3ˊ=−T11x3−T1K1K4x1+T1K1u输出方程:y=x1
写成矢量矩阵形式:
xˊ=⎝⎜⎜⎜⎜⎜⎛00−T1K1K4T3K3−T2100T2K2−T11⎠⎟⎟⎟⎟⎟⎞x+⎝⎜⎜⎜⎜⎛00T1K1⎠⎟⎟⎟⎟⎞uy=(1,0,0)x1
注:带零点环节的处理方法
- 先展开部分分式
- 得到等效方块图
- 再变换成模拟结构图
s+ps+z=1+s+pz−p
1.2 由系统机理建立空间状态描述
步骤:
- 根据系统机理建立微分方程或者差分方程
- 选择有关的物理量作为状态变量
- 导出状态空间表达式
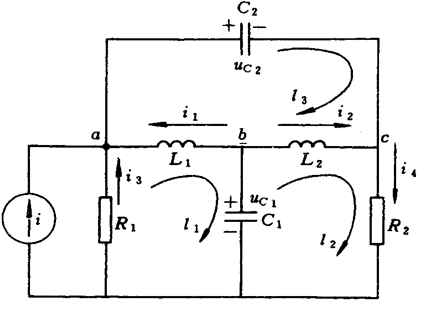
例:电网络如图所示,输入量为电流源,并指定电容
C1 和
C2 上的电压作为输出,求此网络的状态空间表达式。
解:从节点
a、b、c ,按基尔霍夫电流定律列出电流方程:
⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧i+i3+i1−C2uc2ˊ=0C1uc1ˊ+i1+i2=0C2uc2ˊ+i2−i4=0
选取状态变量:
x=⎝⎜⎜⎜⎛x1x2x3x4⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛uc1uc2i1i2⎠⎟⎟⎟⎞
上述电流方程则变为:
⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧i+i3+x3−C2x2ˊ=0C1x1ˊ+x3+x4=0C2x2ˊ+x4−i4=0(7)
从回路
l1、l2、l3 ,按基尔霍夫电压定律列出电压方程:
⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧−L1x3ˊ+x1+R1i3=0−x1+L2x4ˊ+R2i4=0x2−L2x4ˊ+L1x3ˊ=0(8)
(7)和(8)式联立消去独立变量
i3、i4 得:
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧x1ˊ=−C11x3−C11x4R1C2x2ˊ−L1x3ˊ=−x1+R1x3+R1iR2C2x2ˊ+L2x4ˊ=x1−R2x4−Lx3ˊ+L2x4ˊ=x2(9)
(9)式解出
x1ˊ、x2ˊ、x3ˊ、x4ˊ,得到状态空间表达式:


2. 化输入-输出描述为状态空间描述及其几种标准形式
2.1 传递函数没有零点的实现
系统微分方程为:
y(n)+an−1y(n−1)+...+a1yˊ+a0y=b0u(t)
相应系统传递函数:
W(s)=sn+an−1sn−1+...+a1s+a0b0
可选取一组状态变量:
x1ˊ=x2x2ˊ=x3⋮xn−1ˊ=xnxnˊ=−a0x1−a1x2−...−an−2xn−1−an−1xn+u
输出方程:$$y=b_0x_1$$
表示成矩阵形式:
⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛x1ˊx2ˊ⋮xn−1ˊxnˊ⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮0−a010⋮0−a101⋮0−a2⋯⋯⋱⋯⋯00⋮1−an−1⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛x1x2⋮xn−1xn⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞+⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮01⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞u(10)
xˊ=Ax+buy=(b0,0,0,⋯,0)x1
当矩阵A具有A=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮0−a010⋮0−a101⋮0−a2⋯⋯⋱⋯⋯00⋮1−an−1⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞时,称为友矩阵。
友矩阵的特点为:
- 主对角线上方元素均为1
- 最后一行的元素可去任意值
- 其余元素均为0

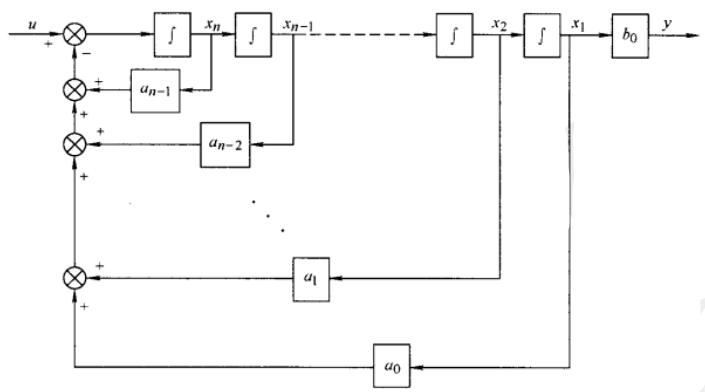
▲ 系统模拟结构图
2.2 传递函数有零点的实现
系统微分方程为:
y(n)+an−1y(n−1)+...+a1yˊ+a0y=bmu(m)+bm−1u(m−1)+...+b1u+ˊb0u
相应系统传递函数:
W(s)=sn+an−1sn−1+...+a1s+a0bmsm+bm−1sm−1+...+b1s+b0,m≤n
在这种包含有输人函数导数情况下的实现问题,与前述实现的不同点主要在于选取合适的结构,使得状态方程中不包含输入函数的导数项,否则将给求解和物理实现带来麻烦。
为了说明方便,又不失一般性,这里先从三阶微分方程出发,找出其实现规律,然后推广到 n 阶系统。
设系统传递函数:
W(s)=U(s)Y(s)=s3+a2s2+a1s+a0b3s3+b2s2+b1s+b0,m=n=3
上式可变换为:
W(s)=b3+s3+a2s2+a1s+a0(b2−a2b3)s2+(b1−a1b3)s+(b0−a0b3),m=n=3令:Y1(s)=s3+a2s2+a1s+a01U(s)则:Y(s)=b3U(s)+Y1(s)[(b2−a2b3)s2+(b1−a1b3)s+(b0−a0b3)]对上式求拉式反变换,可得:y=b3u+(b2−a2b3)y1(2)+(b1−a1b3)y1ˊ+(b0−a0b3)y1
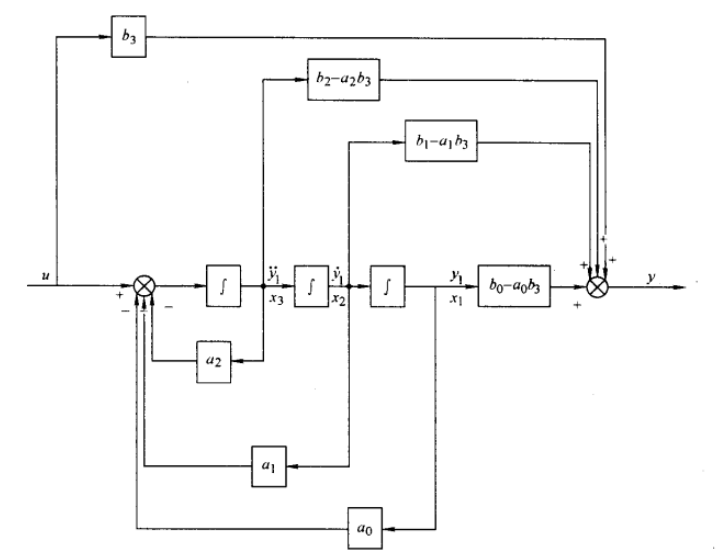
可得系统模拟结构图:

▲ 系统模拟结构图
选取状态变量:
x1ˊ=x2x2ˊ=x3x3ˊ=−a0x1−a1x2−a2x3+uy=b3u+(b2−a2b3)x3+(b1−a1b3)x2+(b0−a0b3)x1
表示成矩阵形式:
⎝⎜⎜⎜⎜⎛x1ˊx2ˊx3ˊ⎠⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎛00−a010−a101−a2⎠⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎛x1x2x3⎠⎟⎟⎟⎟⎞+⎝⎜⎜⎜⎜⎛001⎠⎟⎟⎟⎟⎞u(11)
y=((b0−a0b3),(b1−a1b3),(b2−a2b3))⎝⎜⎜⎜⎜⎛x1x2x3⎠⎟⎟⎟⎟⎞+b3u
推广到 n 阶系统
⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛x1ˊx2ˊ⋮xn−1ˊxnˊ⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮0−a010⋮0−a101⋮0−a2⋯⋯⋱⋯⋯00⋮1−an−1⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛x1x2⋮xn−1xn⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞+⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮01⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞uy=((b0−a0bn),(b1−a1bn),...,(bn−1−an−1bn))⎝⎜⎜⎜⎜⎜⎜⎛x1x2⋮xn−1xn⎠⎟⎟⎟⎟⎟⎟⎞+bnu
本次的分享就到这里

好书不厌百回读,熟读自知其中意。将学习成为习惯,用知识改变命运,用博客见证成长,用行动证明努力。
如果我的博客对你有帮助、如果你喜欢我的博客内容,请 “点赞” “评论” “收藏” 一键三连哦!
听说 👉 点赞 👈 的人运气不会太差,每一天都会元气满满呦!^ _ ^
**码字不易,大家的支持就是我坚持下去的动力。点赞后不要忘了👉关注👈我哦!
如果以上内容有任何错误或者不准确的地方,欢迎在下面👇留个言。或者你有更好的想法,欢迎一起交流学习~~~
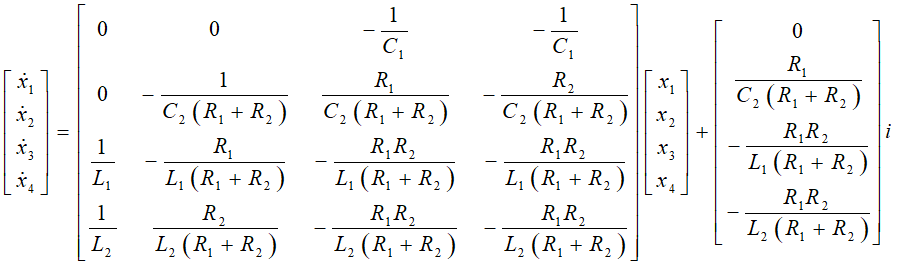
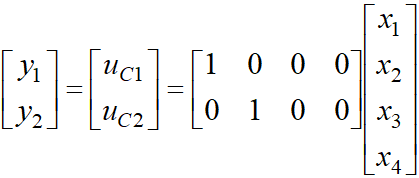



评论(0)