Author:AXYZdong 自动化专业 工科男
有一点思考,有一点想法,有一点理性!
定个小小目标,努力成为习惯!在最美的年华遇见更好的自己!
1.1 状态空间分析法
一组变量→{1、足以完全确定系统运动状态2、个数又是最小
性质:{1、xt=t02、t≥t0时刻的输入It→完全确定在任何t≥t0时刻的状态xt
类似于函数:
xt=f(xt0,It)
- 状态矢量
如果
n 个状态变量用
x1(t),x2(t),...,xn(t) 表示,并把这些状态变量看作是矢量
x(t) 的分量,则称
x(t)为状态矢量,记作:
x(t)=⎝⎜⎜⎜⎜⎛x1(t)x2(t)⋮xn(t)⎠⎟⎟⎟⎟⎞
- 状态空间
以状态变量用
x1(t),x2(t),...,xn(t) 为坐标轴所构成的
n 维空间,称为状态空间。
- 状态方程
由系统的状态变量构成的一阶微分方程组称为系统的状态空间。
例:以
R−L−C 电路说明如何用状态变量描述系统

▲ 图1
有一阶微分方程组:⎩⎪⎨⎪⎧C⋅dtduc=iL⋅dtdi+Ri+uc=u⟹⎩⎪⎨⎪⎧uˊc=C1⋅iiˊ=−L1uc−LRi+L1u(1)
令⎩⎪⎨⎪⎧x1=ucx2=i⟹(x1ˊx2ˊ)=⎝
⎛0−L1C1−LR⎠
⎞(x1x2)+⎝
⎛0L1⎠
⎞u(2)
或:xˊ=Ax+bu
其中:xˊ=(x1ˊx2ˊ),A=⎝
⎛0−L1C1−LR⎠
⎞,b=⎝
⎛0L1⎠
⎞
上述(1)和(2)式分别为图1中系统的 状态方程 和 状态方程的矩阵表达形式。
- 输出方程
在指定系统输出的情况下,该输出与状态变量间的函数关系式,称为系统的输出方程。
在例中系统中,若指定
x1=uc ,则输出方程
y=uc
或:y=x1(3)
矩阵表示形式:
y=(1,0)(x1x2)(4)
- 状态空间表达式
状态方程和输出方程总合起来,构成对一个系统完整的动态描述称为系统的状态空间表达式。
如式(1)和式(3)所示,而式(2)和式(4)就是图1系统的状态空间表达式。
- 单输入——单输出定常系统,矢量矩阵表示时的状态空间表达式为:
xˊ=Ax+buy=cx(5)
式中,
x=⎝⎜⎜⎜⎜⎛x1x2⋮xn⎠⎟⎟⎟⎟⎞为n维状态矢量;A=⎝⎜⎜⎜⎜⎛a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎠⎟⎟⎟⎟⎞为系统内部状态的联系,称为系统矩阵,为n×n方阵;b=⎝⎜⎜⎜⎜⎛b1b2⋮bn⎠⎟⎟⎟⎟⎞为输入对状态的作用,称为输入矩阵或控制矩阵,这里为n×1的列阵;c=(c1,c2,...,cn)为输出矩阵,这里为1×n的行阵。
- 多输入——多输出定常系统,矢量矩阵表示时的状态空间表达式为:
xˊ=Ax+Buy=Cx+Du(6)
式中,x和A同单输入系统,分别n维状态矢量和n×n系统矩阵
u=⎝⎜⎜⎜⎜⎛u1u2⋮ur⎠⎟⎟⎟⎟⎞为r维输入矢量;y=⎝⎜⎜⎜⎜⎛y1y2⋮ym⎠⎟⎟⎟⎟⎞为m维输出矢量;B=⎝⎜⎜⎜⎜⎛b11b21⋮bn1b12b22⋮bn2⋯⋯⋱⋯b1rb2r⋮bnr⎠⎟⎟⎟⎟⎞为n×r输入矩阵;C=⎝⎜⎜⎜⎜⎛c11c21⋮cm1c12c22⋮cm2⋯⋯⋱⋯c1nc2n⋮cmn⎠⎟⎟⎟⎟⎞为m×n输出矩阵;D=⎝⎜⎜⎜⎜⎛d11d21⋮dm1d12d22⋮dm2⋯⋯⋱⋯d1rd2r⋮dmr⎠⎟⎟⎟⎟⎞为m×r直接传递矩阵。为了简便,一般不考虑输入矢量的直接传递,即令D=0

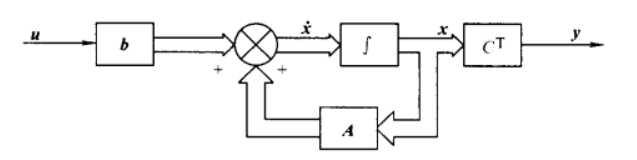
▲ 式5框图

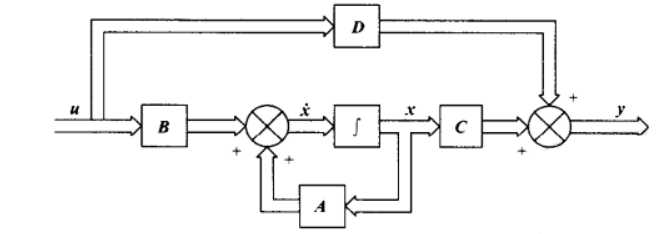
▲ 式6框图
图中单箭头表示标量信号,双箭头表示矢量信号。
1.2 状态结构图
状态空间描述的结构图绘图步骤:
- 画出所有积分器;(积分器的个数等于状态变量的个数,每个积分器的输出表示相应的某个状态变量)
- 根据状态方程和输出方程,画出相应的加法器和比例器;
- 用箭头将这些器件按照一定的顺序连接起来。
常用符号:

例:一阶标量微分方程:
xˊ=ax+bu

▲ 一阶标量微分方程模拟结构图
已知状态空间表达式
x1ˊ=x2x2ˊ=x3x3ˊ=−6x1−3x2−2x3+uy=x1+x2
则系统的模拟结构图为:

本次的分享就到这里

好书不厌百回读,熟读自知其中意。将学习成为习惯,用知识改变命运,用博客见证成长,用行动证明努力。
如果我的博客对你有帮助、如果你喜欢我的博客内容,请 “点赞” “评论” “收藏” 一键三连哦!
听说 👉 点赞 👈 的人运气不会太差,每一天都会元气满满呦!^ _ ^
**码字不易,大家的支持就是我坚持下去的动力。点赞后不要忘了👉关注👈我哦!
如果以上内容有任何错误或者不准确的地方,欢迎在下面👇留个言。或者你有更好的想法,欢迎一起交流学习~~~
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com







评论(0)